AP Statistics Curriculum 2007 Cauchy

General Advance-Placement (AP) Statistics Curriculum - Cauchy Distribution

Cauchy Distribution

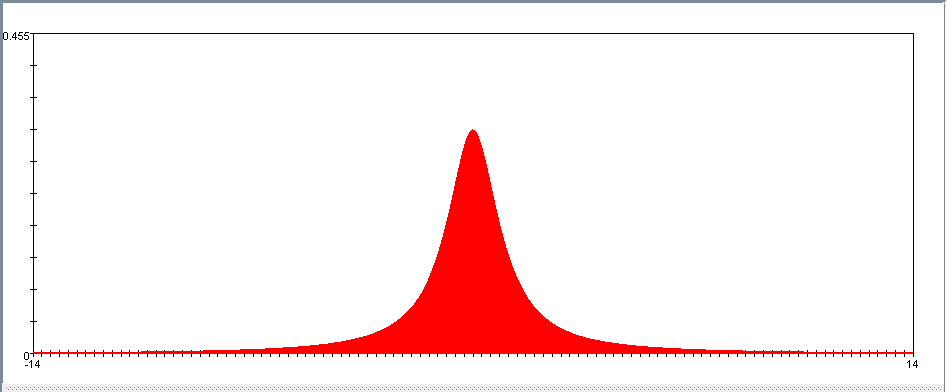
The standard Cauchy distribution is derived from the ratio of two independent Normal distributions. If X ~ N(0,1), and Y ~ N(0,1), then \(\tfrac{X}{Y} \sim Cauchy(0,1)\)

The Cauchy distribution is important in physics (where it’s known as the Lorentz distribution) because it’s the solution to the differential equation describing forced resonance. In spectroscopy, it is the description of the shape of spectral lines which are subject to homogeneous broadening in which all atoms interact in the same way with the frequency range contained in the line shape.

PDF:
\(\frac{1}{\pi\gamma\,\left[1 + \left(\frac{x-x_0}{\gamma}\right)^2\right]}\!\)

CDF:
\(\frac{1}{\pi} \arctan\left(\frac{x-x_0}{\gamma}\right)+\frac{1}{2}\!\)

Mean:
Does Not Exist

Median:
\(x_0\!\)

Variance:
Does Not Exist

Support:
\(x \in (-\infty, +\infty)\!\)

Moment Generating Function Does Not Exist

Applications

\(\cdot\) Used in mechanical and electrical theory, physical anthropology and measurement and calibration problems.

\(\cdot\) In physics it is called a Lorentzian distribution, where it is the distribution of the energy of an unstable state in quantum mechanics.

\(\cdot\) Also used to model the points of impact of a fixed straight line of particles emitted from a point source.

Example

SOCR Links

http://www.distributome.org/ -> SOCR -> Distributions -> Distributome

http://www.distributome.org/ -> SOCR -> Distributions -> Cauchy Distribution

http://www.distributome.org/ -> SOCR -> Functors -> Cauchy Distribution

SOCR Cauchy Distribution calculator (http://socr.ucla.edu/htmls/dist/Cauchy_Distribution.html)

---

• SOCR Home page: http://www.socr.ucla.edu

---

---

Translate this page:

(default)	Deutsch	Español	Français	Italiano	Português	日本語	България	الامارات العربية المتحدة	Suomi	इस भाषा में	Norge
한국어	中文	繁体中文	Русский	Nederlands	Ελληνικά	Hrvatska	Česká republika	Danmark	Polska	România	Sverige