Difference between revisions of "SOCR EduMaterials Activities BMI Modeling Activity"

From SOCR
Jump to: navigation, search
(→‎Data Summary)
(→‎Data Description)
 
(10 intermediate revisions by one other user not shown)
Line 7: Line 7:
  
 
==Summary==
 
==Summary==
−
This activity uses a simplified version of the [[SOCR_Data_BMI_Regression| BMI data sets found here]]. Four cases of data were excluded due to extremely high BMIs that hinted at a mistake in the entry process.  10 variables from the original dataset were left out in the dataset presented here, though the same process presented here may be used on them for additional practice.  
+
This activity uses a simplified version of the [[SOCR_Data_BMI_Regression| BMI data sets found here]]. Four cases of data were excluded due to extremely high BMIs that hinted at a mistake in the entry process.  10 variables from the original dataset were left out in the dataset presented here, though the same process presented here may be used on them for additional practice.
−
 
 
  
 
==Data==
 
==Data==
Line 19: Line 18:
 
** Weight
 
** Weight
 
** BMI—Body Mass Index, calculated as  \( \frac{weight}{height^2} \).
 
** BMI—Body Mass Index, calculated as  \( \frac{weight}{height^2} \).
 +
*** BMI interpretation:
 +
**** Underweight: \( BMI < 18.5\)
 +
**** Normal weight: \( 18.5 \leq BMI \leq 24.9\)
 +
**** Overweight: \(25 \leq BMI \leq 29.9\)
 +
**** Obese: \( 30 \leq BMI\).
  
 
===Data Summary===
 
===Data Summary===
Line 24: Line 28:
 
{| class="wikitable" style="text-align:center; width:30%" border="1"
 
{| class="wikitable" style="text-align:center; width:30%" border="1"
 
|-
 
|-
−
! colspan=2|Underwater_Density_(\( \frac{g}{cm^3}\)) || Body_Fat || Height(m) || Weight_(kg) ||  BMI
+
! Statistic || Underwater_Density_(\( \frac{g}{cm^3}\)) || Body_Fat || Height(m) || Weight_(kg) ||  BMI
 
|-
 
|-
 
| Mean || 1.0562 || 18.854 || 1.787 || 80.547 || 25.18643319
 
| Mean || 1.0562 || 18.854 || 1.787 || 80.547 || 25.18643319
Line 537: Line 541:
  
 
==[[AP_Statistics_Curriculum_2007_EDA_Pics|Exploratory data analyses (EDA)]]==
 
==[[AP_Statistics_Curriculum_2007_EDA_Pics|Exploratory data analyses (EDA)]]==
−
Various data patterns may be observed and explored using different types of graphical tools for plotting variables. Which of the following graphs are more or less likely to demonstrate visually significant grouping differences?
+
Before we run any quantitative tests, let’s examine what these variables look like in graphical form. Keep an eye out for which variables appear to follow a normal distribution.
 +
 
 +
<center>[[Image:SOCR_Activity_BMI_ChiSquare_Fig2.png|700px]]</center>
 +
 
 +
==Quantitative Data Analyses (QDA)==
 +
In this section, we will be testing the BMI variable for normality, although the same analysis can be carried for the other variables. As the name '''goodness-of-fit''' implies, we first need to create a normal model to compare to. We will use the sample mean (25.18643319) and standard deviation (3.146481308) as the parameters of the normal distribution.
 +
 
 +
The next few steps will use the [http://socr.ucla.edu/htmls/SOCR_Distributions.html SOCR Distributions Applet] (see [[SOCR_EduMaterials_DistributionsActivities|Distribution Activities]]). Open the [http://socr.ucla.edu/htmls/SOCR_Distributions.html applet] in a java-enabled browser.
 +
 
 +
<center>[[Image:SOCR_Activity_BMI_ChiSquare_Fig3.png|500px]]</center>
 +
 
 +
===Data Modeling===
 +
Enter in the values for the mean and standard deviation, then drag the graph down to see your full distribution.
 +
 
 +
<center>[[Image:SOCR_Activity_BMI_ChiSquare_Fig4.png|500px]]</center>
 +
 
 +
To run a goodness of fit test, we will need to create a set of bins to compare between the real distribution and the '''expected''' normal one. For simplicity’s sake, we will use a 16 bins of bin-size 1 beginning with BMI=18 and ending with BMI=34. To find the frequency of results in each bin from the normal distribution, click on the edges of the bin size (try to be as accurate as possible) on the normal distribution applet. The example shown alternatively, use the [[AP_Statistics_Curriculum_2007_Normal_Std|normal CDF function]].
 +
 
 +
<center>[[Image:SOCR_Activity_BMI_ChiSquare_Fig5.png|500px]]</center>
 +
 
 +
After calculating the probability of each bin, multiply each of these probabilities by the total number of cases (in this case, 248). Now we can place these calculated frequencies next to the frequencies from the observed distribution (the observed frequencies were found by plain counting):
 +
 
 +
<center>
 +
{| class="wikitable" style="text-align:center; width:30%" border="1"
 +
|-
 +
!Bin(Simplified)||Bin(Actual)||Normal_Probability||EstimatedNormalFrequency||ObservedFrequency
 +
|-
 +
|18-19||18.000-18.999||0.013454035||3.39041682||1
 +
|-
 +
|19-20||19.000-19.999||0.025001757||6.300442764||6
 +
|-
 +
|20-21||20.000-20.999||0.042032155||10.59210306||11
 +
|-
 +
|21-22||21.000-21.999||0.06392769||16.10977788||23
 +
|-
 +
|22-23||22.000-22.999||0.087962245||22.16648574||20
 +
|-
 +
|23-24||23.000-23.999||0.109497598||27.5933947||38
 +
|-
 +
|24-25||24.000-24.999||0.123313845||31.07508894||26
 +
|-
 +
|25-26||25.000-25.999||0.125638222||31.66083194||31
 +
|-
 +
|26-27||26.000-26.999||0.115806485||29.18323422||26
 +
|-
 +
|27-28||27.000-27.999||0.096570457||24.33575516||21
 +
|-
 +
|28-29||28.000-28.999||0.072854419||18.35931359||9
 +
|-
 +
|29-30||29.000-29.999||0.049724263||12.53051428||15
 +
|-
 +
|30-31||30.000-30.999||0.030702836||7.737114672||10
 +
|-
 +
|31-32||31.000-31.999||0.017150734||4.321984968||6
 +
|-
 +
|32-33||32.000-32.999||0.008667207||2.184136164||2
 +
|-
 +
|33-34||33.000-33.999||0.00396249||0.99854748||3
 +
|}
 +
</center>
 +
 
 +
It might be useful to see how this hypothetical '''expected''' data matches up with our actual results graphically. Note the differences between the two data sets in the Quantile-Quantile Charts (ignore the ''stacked'' shape of the normal estimation, which is due to binning the data). Note that the line is a better fit in the latter case).
 +
 
 +
<center>[[Image:SOCR_Activity_BMI_ChiSquare_Fig6.png|500px]]</center>
 +
 
 +
===Chi-Square Goodness-of-Fit Test===
 +
With these values now settled, we can begin the [[AP_Statistics_Curriculum_2007_Contingency_Fit|Chi-square analysis]]. Open up the [http://socr.ucla.edu/htmls/SOCR_Analyses.html SOCR Analyses Applet] in a Java-enabled browser, and then select the '''Chi-square Goodness of Fit''' in the pull-down menu on the left:
 +
 
 +
<center>[[Image:SOCR_Activity_BMI_ChiSquare_Fig7.png|500px]]</center>
 +
 
 +
Next, enter the data into two columns using the '''Paste''' button.
 +
 
 +
<center>[[Image:SOCR_Activity_BMI_ChiSquare_Fig8.png|500px]]</center>
 +
 
 +
Name the two columns '''Observed''' (for the actual results) and '''Expected''' (for the normal model estimates).
 +
 
 +
<center>[[Image:SOCR_Activity_BMI_ChiSquare_Fig9.png|500px]]</center>
 +
 
 +
Click on the '''Mapping''' tab and add observed and expected into the correct bins.
 +
 
 +
<center>[[Image:SOCR_Activity_BMI_ChiSquare_Fig10.png|500px]]</center>
 +
 
 +
Click the '''Calculate''' Button. A window should pop up asking about the number of parameters. Recall that the normal distribution is defined by two parameters—mean and standard deviation. Enter “2” and press “OK”.
 +
 
 +
<center>[[Image:SOCR_Activity_BMI_ChiSquare_Fig11.png|500px]]</center>
 +
 
 +
The results page should come up with the following text:
 +
: Observed Data = Observed
 +
: Expected Data = Expected
 +
Chi-Square Goodness of Fit Results:
 +
: Total Counts = 16
 +
: Number of Parameters = 2
 +
: Chi-Square Goodness of Fit Results:
 +
: ********** Chi-Square Statistic is: 21.044 *********
 +
: ********** Chi-Square Degrees of Freedom is: 16 - 2 - 1 = 13 *********
 +
: ********** Chi-Square p-value is: '''.072''' *********
 +
 
 +
Based on ''α =  0.05'', there is not enough evidence to conclude that the BMI data distribution does not fit a normal distribution. However, it is worth noting that it does come very close. This understanding of a distribution is very important to health officials; for example, it helps creates the charts that doctors national-wide use to understand. In addition, a deviation from that distribution can be used to chart changes in the overall health of the nation ([[SOCR_EduMaterials_Activities_BMI_Modeling_Activity#References|Penman, 2006]]).
 +
 
 +
===Linear Regression===
 +
Finally, we can explore the correlation between the observed frequencies and the prediction-model values (predicted frequencies) of the BMI data within each of the 16 bins. If there is a good agreement (e.g., high correlation) this would indicate that the normal distribution model fits well the observed data (BMI frequencies).
 +
 
 +
Copy and paste the 2 column data (observed and predicted frequencies) into the [http://www.socr.ucla.edu/htmls/ana/SimpleRegression_Analysis.html Simple Linear Regression applet] of [http://socr.ucla.edu/htmls/SOCR_Analyses.html SOCR Analysis].
 +
 
 +
<center>[[Image:SOCR_Activity_BMI_ChiSquare_Fig12.png|500px]]</center>
 +
 
 +
Map the predicted and observed frequencies to the Dependent and Independent variables ('''Mapping''' Tab).
 +
 +
<center>[[Image:SOCR_Activity_BMI_ChiSquare_Fig13.png|500px]]</center>
 +
 
 +
Click '''Calculate''' button to view the results.
 +
'''Regression Model''': 
 +
: PredictedFreq = 1.71070 + 0.8918062570205698 * ObservedFreq
 +
: Correlation(ObservedFreq, PredictedFreq) = .91394
 +
: R-Square = .83529
 +
: Intercept:
 +
:: Parameter Estimate: 1.71070
 +
:: Standard Error:    2.00468
 +
:: T-Statistics:        .85335
 +
:: P-Value:            .40783
 +
: Slope:
 +
:: Parameter Estimate: .89181
 +
:: Standard Error:    .10584
 +
:: T-Statistics:        8.42598
 +
:: P-Value:            .00000
 +
 
 +
===Regression Graphs===
 +
The '''Graphs''' tab includes a regression model plot, scatter plot with confidence/prediction limits, and various plots of the residuals.
 +
 
 +
<center>[[Image:SOCR_Activity_BMI_ChiSquare_Fig14.png|500px]]</center>
  
−
<center>[[Image:SOCR_Activity_ANOVA_SnailsSexualDimorphism_Fig1.jpg|500px]]</center>
+
<center>[[Image:SOCR_Activity_BMI_ChiSquare_Fig15.png|500px]]</center>
  
 +
<center>[[Image:SOCR_Activity_BMI_ChiSquare_Fig16.png|500px]]</center>
  
−
==Conclusions==
+
<center>[[Image:SOCR_Activity_BMI_ChiSquare_Fig17.png|500px]]</center>
  
 +
<center>[[Image:SOCR_Activity_BMI_ChiSquare_Fig18.png|500px]]</center>
  
 
==Practice problems==
 
==Practice problems==
−
*  
+
* Try this method out on one of the other variables. See if it breaks from the normal distribution.
 +
* Many biological measures are said to follow a normal distribution. Look under the data header “Biomedical Data” in the SOCR Free Datasets and check this claim out with one of the variables you are interested in.
  
 
==See also==
 
==See also==
−
*  
+
* [[SOCR_EduMaterials_AnalysisActivities_Chi_Goodness| SOCR Chi-Square Goodness-of-Fit Test]]
 +
* [[AP_Statistics_Curriculum_2007_Contingency_Fit| SOCR EBook, Chi-Square Modeling]]
  
 
==References==
 
==References==
−
*  
+
* K.W. Penrose, A.G. Nelson, A.G. Fisher, FACSM, Human Performance Research Center, Brigham Young University, Provo, Utah 84602 as listed in Medicine and Science in Sports and Exercise, vol. 17, no. 2, April 1985, p. 189.
 +
* A.D. Penman and W.D. Johnson. [http://www.ncbi.nlm.nih.gov/pmc/articles/pmc1636707/ Changing shape of the body mass index distribution curve in the population: implications for public health policy to reduce the prevalence of adult obesity],  Preventing chronic disease, vol. 3, no. 2, 2006.
  
 
{{translate|pageName=http://wiki.stat.ucla.edu/socr/index.php?title=SOCR_EduMaterials_Activities_BMI_Modeling_Activity}}
 
{{translate|pageName=http://wiki.stat.ucla.edu/socr/index.php?title=SOCR_EduMaterials_Activities_BMI_Modeling_Activity}}

Latest revision as of 14:52, 1 July 2014

SOCR Educational Materials - Activities - SOCR Body Mass Index (BMI) Activity and Applications of the Chi-Squared Test

Often times when solving a problem from intro-level textbooks, we are told to assume that a population follows a normal distribution. Other times, a graph of the data will allow us to assume some degree of normality. This allows the use of a number of statistical analyses later on.

Motivation and Goals

The following activity will demonstrate one of the ways to test for normality, using the Chi-Squared test for Goodness-of-Fit. The model to fit will be the normal model. We will run this test on a human characteristic often assumed to fit at least some kind of normal model: BMI.

Summary

This activity uses a simplified version of the BMI data sets found here. Four cases of data were excluded due to extremely high BMIs that hinted at a mistake in the entry process. 10 variables from the original dataset were left out in the dataset presented here, though the same process presented here may be used on them for additional practice.

Data

Data Description

  • Number of cases: 248
  • Variables
    • Underwater Density – Density determined via a graduated-cylinder type test
    • Body fat—Calculated body density and tissue-type proportions using Siri’s equation (see the full dataset page)
    • Height
    • Weight
    • BMI—Body Mass Index, calculated as \( \frac{weight}{height^2} \).
      • BMI interpretation:
        • Underweight: \( BMI < 18.5\)
        • Normal weight: \( 18.5 \leq BMI \leq 24.9\)
        • Overweight: \(25 \leq BMI \leq 29.9\)
        • Obese: \( 30 \leq BMI\).

Data Summary

Statistic Underwater_Density_(\( \frac{g}{cm^3}\)) Body_Fat Height(m) Weight_(kg) BMI
Mean 1.0562 18.854 1.787 80.547 25.18643319
SD 0.0184 8.0663 0.0659 12.0076 3.146481308

Raw Dataset

Underwater_Density(g/cm3) Body_Fat Height(m) Weight(kg) BMI
1.0708 12.3 1.72085 69.96662 23.6268
1.0853 6.1 1.83515 78.58488 23.33436
1.0414 25.3 1.68275 69.85322 24.66876
1.0751 10.4 1.83515 83.80119 24.88325
1.034 28.7 1.80975 83.57439 25.51738
1.0502 20.9 1.89865 95.3678 26.45525
1.0549 19.2 1.77165 82.10022 26.15703
1.0704 12.4 1.8415 79.83226 23.54155
1.09 4.1 1.8796 86.63614 24.5227
1.0722 11.7 1.8669 89.92469 25.80102
1.083 7.1 1.8923 84.48158 23.59294
1.0812 7.8 1.9304 97.97595 26.29208
1.0513 20.8 1.7653 81.87342 26.27277
1.0505 21.2 1.80975 93.09983 28.42574
1.0484 22.1 1.7653 85.16197 27.32805
1.0512 20.9 1.6764 73.82216 26.26827
1.0333 29 1.8034 88.79071 27.3013
1.0468 22.9 1.8034 94.9142 29.18415
1.0622 16 1.72085 83.3476 28.14538
1.061 16.5 1.8669 96.04818 27.55796
1.0551 19.1 1.7272 81.19303 27.21658
1.064 15.2 1.77165 90.94527 28.97505
1.0631 15.6 1.73355 63.61633 21.16878
1.0584 17.7 1.778 67.47187 21.34319
1.0668 14 1.72085 68.60585 23.16728
1.0911 3.7 1.8161 72.23458 21.90109
1.0811 7.9 1.7145 59.6474 20.29161
1.0468 22.9 1.7145 67.13167 22.83771
1.091 3.7 1.64465 60.44118 22.34529
1.079 8.8 1.7526 72.91497 23.73838
1.0716 11.9 1.87325 82.55381 23.52587
1.0862 5.7 1.80975 72.68818 22.19354
1.0719 11.8 1.80975 76.20352 23.26686
1.0502 21.3 1.8034 99.10993 30.47425
1.0263 32.3 1.8669 112.1507 32.17806
1.0101 40.1 1.651 86.97634 31.90854
1.0438 24.2 1.778 91.73906 29.01956
1.0346 28.4 1.73355 89.2443 29.69667
1.0258 32.6 1.7018 92.07925 31.79397
1.0279 31.6 1.778 98.42954 31.13594
1.0269 32 1.8161 96.16158 29.15561
1.0814 7.7 1.7272 56.81244 19.044
1.067 13.9 1.86055 74.50255 21.52229
1.0742 10.8 1.7145 60.55458 20.60023
1.0665 5.6 1.80975 67.35847 20.56625
1.0678 13.6 1.7399 61.57516 20.34028
1.0903 4 1.69545 57.83303 20.11898
1.0756 10.2 1.83515 71.78099 21.31407
1.084 6.6 1.7526 63.16274 20.56342
1.0807 8 1.72085 62.25555 21.02287
1.0848 6.3 1.8669 69.28623 19.87947
1.0906 3.9 1.7145 61.80196 21.02458
1.0473 22.6 1.8288 89.81129 26.85335
1.0524 20.4 1.7272 82.32702 27.5967
1.0356 28 1.7653 91.28546 29.29305
1.028 31.5 1.79705 91.85245 28.44267
1.043 24.6 1.67005 81.53323 29.23316
1.0396 26.1 1.86055 97.97595 28.30328
1.0317 29.8 1.7399 81.07964 26.78325
1.0298 30.7 1.78435 87.65673 27.5312
1.0403 25.8 1.7018 80.73944 27.87845
1.0264 32.3 1.778 93.21323 29.48588
1.0313 30 1.7145 83.2342 28.31567
1.0499 21.5 1.79705 68.71924 21.27933
1.0673 13.8 1.8161 70.19342 21.28222
1.0847 6.3 1.75895 70.42022 22.76095
1.0693 12.9 1.8161 71.1006 21.55727
1.0439 24.3 1.8161 75.97672 23.03568
1.0788 8.8 1.74625 66.56468 21.82886
1.0796 8.5 1.87325 72.91497 20.77903
1.068 13.5 1.6256 56.69905 21.45598
1.072 11.8 1.67005 64.86371 23.25642
1.0666 18.5 1.7145 67.24507 22.87628
1.079 8.8 1.7653 73.70876 23.65277
1.0483 22.2 1.7399 80.62604 26.63341
1.0498 21.5 1.78435 73.14177 22.97235
1.056 18.8 1.75895 77.67769 25.10668
1.0283 31.4 1.72085 74.27575 25.08193
1.0382 26.8 1.70815 68.15225 23.3576
1.0568 18.4 1.84785 86.29595 25.27301
1.0377 27 1.778 77.4509 24.49982
1.0378 27 1.75895 76.20352 24.63021
1.0386 26.6 1.7145 75.74993 25.76958
1.0648 14.9 1.70815 71.5542 24.52354
1.0462 23.1 1.67005 72.57478 26.02117
1.08 8.3 1.8415 80.17245 23.64186
1.0666 14.1 1.8542 79.83226 23.22016
1.052 20.5 1.778 80.28585 25.3966
1.0573 18.2 1.7653 81.53323 26.16361
1.0795 8.5 1.7907 74.95614 23.37553
1.0424 24.9 1.82245 87.31653 26.28968
1.0785 9 1.8923 83.57439 23.33959
1.0991 17.4 1.97485 101.8315 26.11042
1.077 9.6 1.86055 85.61556 24.73261
1.073 11.3 1.6891 73.70876 25.83499
1.0582 17.8 1.73355 70.98721 23.62149
1.0484 22.2 1.8288 89.3577 26.71773
1.0506 21.2 1.8669 90.03809 25.83355
1.0524 20.4 1.8288 78.81167 23.56449
1.053 20.1 1.80975 78.35808 23.92471
1.048 22.3 1.87325 89.2443 25.4325
1.0412 25.4 1.75895 80.28585 25.94968
1.0578 18 1.7399 75.06954 24.79792
1.0547 19.3 1.8669 90.83187 26.0613
1.0569 18.3 1.88595 92.19265 25.92006
1.0593 17.3 1.9177 87.99692 23.92799
1.05 21.4 1.75895 76.43031 24.70351
1.0538 19.7 1.7399 77.4509 25.58456
1.0355 28 1.778 83.1208 26.29337
1.0486 22.1 1.778 80.85284 25.57595
1.0503 21.3 1.78435 73.93556 23.22166
1.0384 26.7 1.82245 79.49206 23.93385
1.0607 16.7 1.75895 71.66759 23.16412
1.0529 20.1 1.84785 80.39925 23.54608
1.0671 13.9 1.8288 81.19303 24.27651
1.0404 25.8 1.8796 86.63614 24.5227
1.0575 18.1 1.83515 85.04857 25.25363
1.0358 27.9 1.8923 93.66682 26.15808
1.0414 25.3 1.8161 84.02799 25.47678
1.0652 14.7 1.74625 72.68818 23.83696
1.0623 16 1.69545 68.71924 23.90608
1.0674 13.8 1.6891 73.02837 25.59652
1.0587 17.5 1.7018 75.74993 26.15563
1.0373 27.2 1.74625 80.51265 26.40288
1.059 17.4 1.72085 69.05944 23.32046
1.0515 20.8 1.86055 87.20313 25.19123
1.0648 14.9 1.77165 74.95614 23.88094
1.0575 18.1 1.8161 77.90449 23.62017
1.0472 22.7 1.7907 77.67769 24.22427
1.0452 23.6 1.86055 89.3577 25.81364
1.0398 26.1 1.69545 71.214 24.77396
1.0435 24.4 1.7653 76.31692 24.48972
1.0374 27.1 1.77165 84.36818 26.8796
1.0491 21.8 1.79705 75.63653 23.42131
1.0325 29.4 1.8796 85.16197 24.10543
1.0481 22.4 1.80975 76.31692 23.30149
1.0522 20.4 1.905 96.50178 26.59165
1.0422 24.9 1.8034 80.17245 24.65137
1.0571 18.3 1.7653 78.58488 25.2175
1.0459 23.3 1.72085 75.74993 25.57974
1.0775 9.4 1.83515 72.46138 21.5161
1.0754 10.3 1.9685 85.3434 22.02415
1.0664 14.2 1.79705 70.76041 21.91139
1.055 19.2 1.84785 94.57401 27.69736
1.0322 29.6 1.77165 93.66682 29.84214
1.0873 5.3 1.8415 65.2039 19.22782
1.0416 25.2 1.78435 101.1511 31.76951
1.0776 9.4 1.7526 69.05944 22.48316
1.0542 19.6 1.8923 109.656 30.62333
1.0758 10.1 1.83515 66.22449 19.66416
1.061 16.5 1.70815 71.1006 24.36808
1.051 21 1.8669 90.83187 26.0613
1.0594 17.3 1.91135 77.79109 21.29362
1.0287 31.2 1.7526 93.32663 30.38365
1.0761 10 1.83515 82.78061 24.5802
1.0704 12.5 1.74625 61.91536 20.30419
1.0477 22.5 1.8161 80.39925 24.37656
1.0775 9.4 1.83515 68.60585 20.37127
1.0653 14.6 1.8542 88.9041 25.85882
1.069 13 1.74625 83.57439 27.40693
1.0644 15.1 1.7907 63.50293 19.80378
1.037 27.3 1.8288 99.22333 29.66753
1.0549 19.2 1.87325 98.42954 28.05007
1.0492 21.8 1.7272 75.40973 25.27797
1.0525 20.3 1.83515 101.9449 30.27069
1.018 34.3 1.7653 103.5325 33.22306
1.061 16.5 1.7653 78.35808 25.14472
1.0926 3 1.72085 69.05944 23.32046
1.0983 0.7 1.6637 57.03924 20.60742
1.0521 20.5 1.8034 80.39925 24.7211
1.0603 16.9 1.8161 79.94566 24.23904
1.0414 25.3 1.82245 102.8521 30.9672
1.0763 9.9 1.75895 65.88429 21.29486
1.0689 13.1 1.7018 68.49245 23.6497
1.0316 29.9 1.8161 109.4292 33.17827
1.0477 22.5 1.75895 84.93517 27.45242
1.0603 16.9 1.8923 106.4808 29.7366
1.0387 26.6 1.88595 99.45013 27.9605
1.1089 0 1.7272 53.7507 18.01768
1.0725 11.5 1.70815 66.11109 22.65804
1.0713 12.1 1.77165 72.23458 23.01385
1.0587 17.5 1.88595 77.3375 21.74352
1.0794 8.6 1.8161 75.97672 23.03568
1.0453 23.6 1.88595 105.5736 29.68212
1.0524 20.4 1.8288 95.48119 28.54864
1.052 20.5 1.8415 91.73906 27.05271
1.0434 24.4 1.73355 83.91459 27.92317
1.0728 11.4 1.75895 69.39963 22.43108
1.014 38.1 1.9304 110.7899 29.73073
1.0624 15.9 1.7907 87.77012 27.37165
1.0429 24.7 1.89865 101.9449 28.27976
1.047 22.8 1.84785 73.82216 21.61988
1.0411 25.5 1.73355 81.64663 27.16849
1.0488 22 1.7526 70.87381 23.07386
1.0583 17.7 1.8161 76.20352 23.10444
1.0841 6.6 1.84785 75.86332 22.21767
1.0462 23.6 1.7145 77.4509 26.34823
1.0709 12.2 1.78435 80.85284 25.39424
1.0484 22.1 1.75895 68.03886 21.99126
1.034 28.7 1.8161 90.94527 27.57405
1.0854 6 1.8796 83.461 23.62396
1.0209 34.8 1.77165 101.1511 32.22662
1.061 16.6 1.8542 94.68741 27.54096
1.025 32.9 1.6637 75.29633 27.20344
1.0254 32.8 1.8415 88.45051 26.08296
1.0771 9.6 1.78435 72.80158 22.8655
1.0742 10.8 1.79705 72.46138 22.43811
1.0829 7.1 1.7272 63.72973 21.36273
1.0373 27.2 1.8923 98.08935 27.39314
1.0543 19.5 1.82245 76.31692 22.97786
1.0561 18.7 1.79705 88.33711 27.35413
1.0543 19.5 1.8542 78.35808 22.79138
1.0678 13.6 1.77165 67.69866 21.56871
1.0819 7.5 1.778 70.08002 22.16821
1.0433 24.5 1.82245 90.37828 27.21152
1.0646 15 1.75895 70.08002 22.65099
1.0706 12.4 1.7907 69.51303 21.67807
1.0399 26 1.83515 104.3262 30.97778
1.0726 11.5 1.7145 73.36857 24.95945
1.0874 5.2 1.70815 64.52351 22.11393
1.074 10.9 1.74625 81.53323 26.73756
1.0703 12.5 1.69545 57.37943 19.96118
1.065 14.8 1.73355 76.88391 25.58366
1.0418 25.2 1.88595 90.03809 25.3143
1.0647 14.9 1.7653 79.15187 25.39944
1.0601 17 1.7399 76.09012 25.13505
1.0745 10.6 1.67005 67.01827 24.02892
1.062 16.1 1.82245 82.66721 24.88984
1.0636 15.4 1.8161 79.60546 24.13589
1.0384 26.7 1.70815 73.36857 25.14537
1.0403 25.8 1.7145 71.5542 24.34222
1.0563 18.6 1.7145 76.54371 26.03961
1.0424 24.8 1.83515 86.86294 25.79238
1.0372 27.3 1.7653 99.40477 31.89849
1.0705 12.4 1.7653 70.42022 22.5975
1.0316 29.9 1.67005 86.06915 30.85948
1.0599 17 1.67005 57.83303 20.73562
1.0207 35 1.73355 101.8315 33.88515
1.0304 30.4 1.8288 106.254 31.76968
1.0256 32.6 1.84785 103.3057 30.25456
1.0334 29 1.7399 90.49168 29.89235
1.0641 15.2 1.75895 70.53361 22.7976
1.0308 30.2 1.7907 97.74916 30.48368
1.0736 11 1.7018 60.89478 21.02631
1.0236 33.6 1.77165 91.17207 29.04731
1.0328 29.3 1.6764 84.70838 30.14193
1.0399 26 1.7907 86.52274 26.98265
1.0271 31.9 1.778 94.12042 29.77285

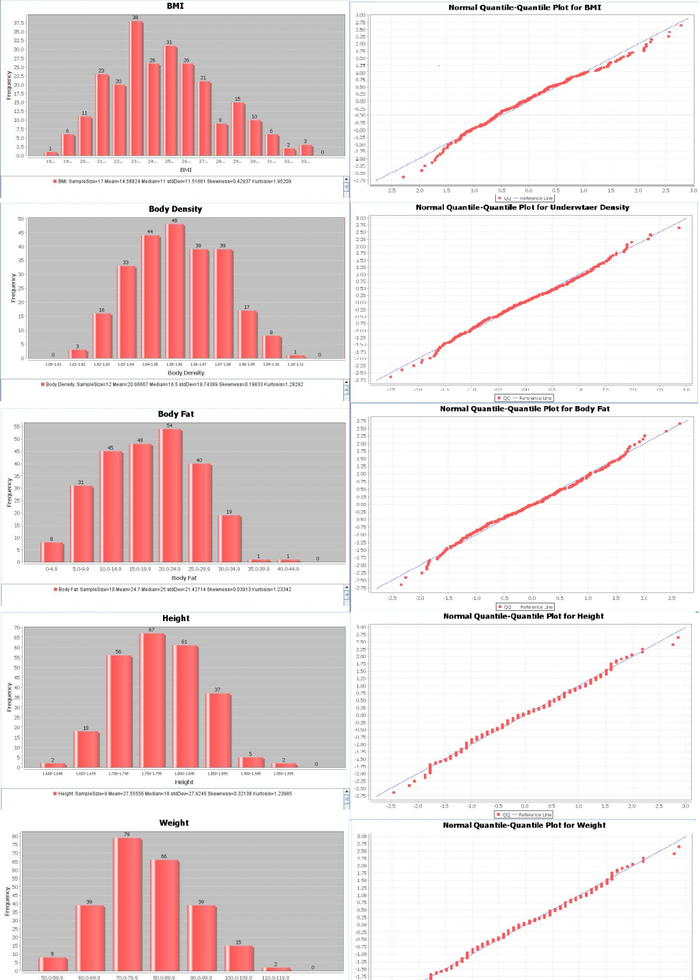
Exploratory data analyses (EDA)

Before we run any quantitative tests, let’s examine what these variables look like in graphical form. Keep an eye out for which variables appear to follow a normal distribution.

SOCR Activity BMI ChiSquare Fig2.png

Quantitative Data Analyses (QDA)

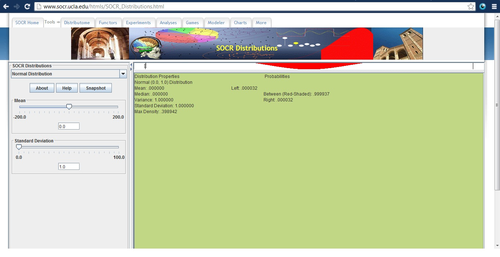
In this section, we will be testing the BMI variable for normality, although the same analysis can be carried for the other variables. As the name goodness-of-fit implies, we first need to create a normal model to compare to. We will use the sample mean (25.18643319) and standard deviation (3.146481308) as the parameters of the normal distribution.

The next few steps will use the SOCR Distributions Applet (see Distribution Activities). Open the applet in a java-enabled browser.

SOCR Activity BMI ChiSquare Fig3.png

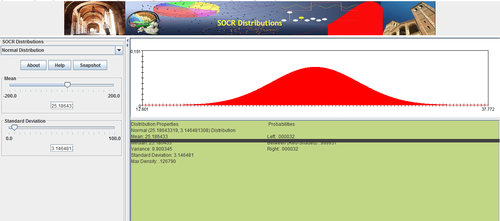
Data Modeling

Enter in the values for the mean and standard deviation, then drag the graph down to see your full distribution.

SOCR Activity BMI ChiSquare Fig4.png

To run a goodness of fit test, we will need to create a set of bins to compare between the real distribution and the expected normal one. For simplicity’s sake, we will use a 16 bins of bin-size 1 beginning with BMI=18 and ending with BMI=34. To find the frequency of results in each bin from the normal distribution, click on the edges of the bin size (try to be as accurate as possible) on the normal distribution applet. The example shown alternatively, use the normal CDF function.

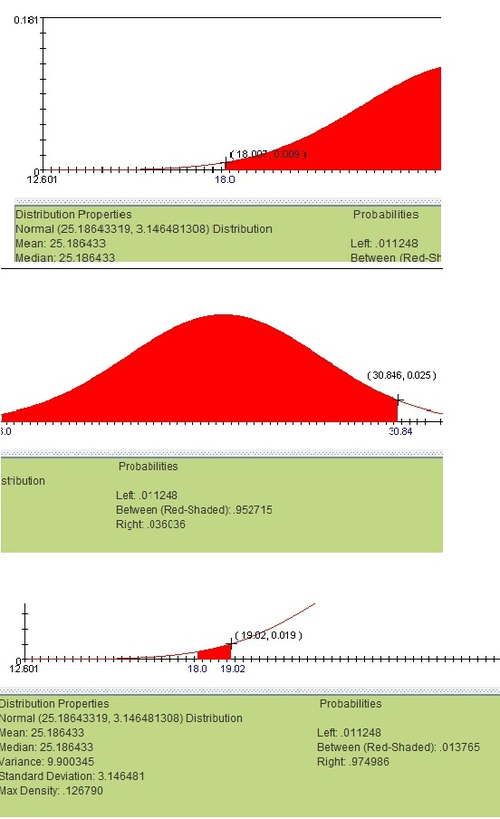
SOCR Activity BMI ChiSquare Fig5.png

After calculating the probability of each bin, multiply each of these probabilities by the total number of cases (in this case, 248). Now we can place these calculated frequencies next to the frequencies from the observed distribution (the observed frequencies were found by plain counting):

Bin(Simplified) Bin(Actual) Normal_Probability EstimatedNormalFrequency ObservedFrequency
18-19 18.000-18.999 0.013454035 3.39041682 1
19-20 19.000-19.999 0.025001757 6.300442764 6
20-21 20.000-20.999 0.042032155 10.59210306 11
21-22 21.000-21.999 0.06392769 16.10977788 23
22-23 22.000-22.999 0.087962245 22.16648574 20
23-24 23.000-23.999 0.109497598 27.5933947 38
24-25 24.000-24.999 0.123313845 31.07508894 26
25-26 25.000-25.999 0.125638222 31.66083194 31
26-27 26.000-26.999 0.115806485 29.18323422 26
27-28 27.000-27.999 0.096570457 24.33575516 21
28-29 28.000-28.999 0.072854419 18.35931359 9
29-30 29.000-29.999 0.049724263 12.53051428 15
30-31 30.000-30.999 0.030702836 7.737114672 10
31-32 31.000-31.999 0.017150734 4.321984968 6
32-33 32.000-32.999 0.008667207 2.184136164 2
33-34 33.000-33.999 0.00396249 0.99854748 3

It might be useful to see how this hypothetical expected data matches up with our actual results graphically. Note the differences between the two data sets in the Quantile-Quantile Charts (ignore the stacked shape of the normal estimation, which is due to binning the data). Note that the line is a better fit in the latter case).

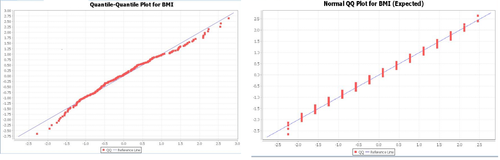
SOCR Activity BMI ChiSquare Fig6.png

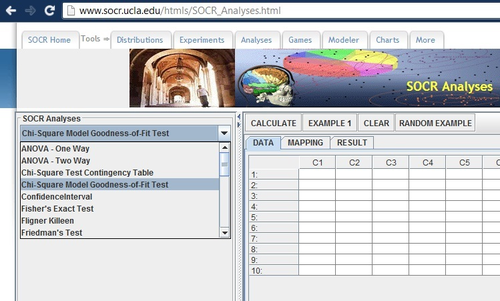
Chi-Square Goodness-of-Fit Test

With these values now settled, we can begin the Chi-square analysis. Open up the SOCR Analyses Applet in a Java-enabled browser, and then select the Chi-square Goodness of Fit in the pull-down menu on the left:

SOCR Activity BMI ChiSquare Fig7.png

Next, enter the data into two columns using the Paste button.

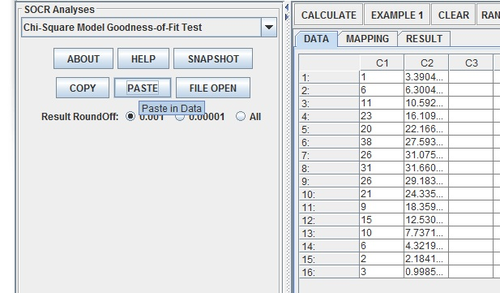
SOCR Activity BMI ChiSquare Fig8.png

Name the two columns Observed (for the actual results) and Expected (for the normal model estimates).

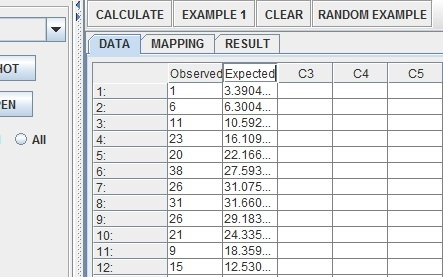
SOCR Activity BMI ChiSquare Fig9.png

Click on the Mapping tab and add observed and expected into the correct bins.

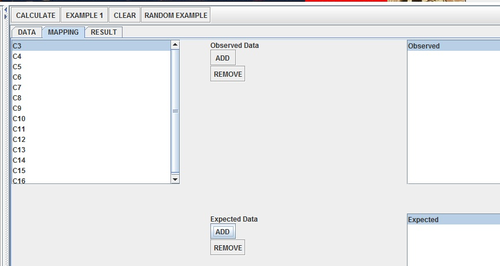
SOCR Activity BMI ChiSquare Fig10.png

Click the Calculate Button. A window should pop up asking about the number of parameters. Recall that the normal distribution is defined by two parameters—mean and standard deviation. Enter “2” and press “OK”.

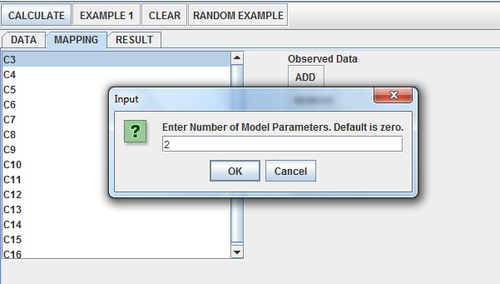
SOCR Activity BMI ChiSquare Fig11.png

The results page should come up with the following text:

Observed Data = Observed
Expected Data = Expected

Chi-Square Goodness of Fit Results:

Total Counts = 16
Number of Parameters = 2
Chi-Square Goodness of Fit Results:
********** Chi-Square Statistic is: 21.044 *********
********** Chi-Square Degrees of Freedom is: 16 - 2 - 1 = 13 *********
********** Chi-Square p-value is: .072 *********

Based on α = 0.05, there is not enough evidence to conclude that the BMI data distribution does not fit a normal distribution. However, it is worth noting that it does come very close. This understanding of a distribution is very important to health officials; for example, it helps creates the charts that doctors national-wide use to understand. In addition, a deviation from that distribution can be used to chart changes in the overall health of the nation (Penman, 2006).

Linear Regression

Finally, we can explore the correlation between the observed frequencies and the prediction-model values (predicted frequencies) of the BMI data within each of the 16 bins. If there is a good agreement (e.g., high correlation) this would indicate that the normal distribution model fits well the observed data (BMI frequencies).

Copy and paste the 2 column data (observed and predicted frequencies) into the Simple Linear Regression applet of SOCR Analysis.

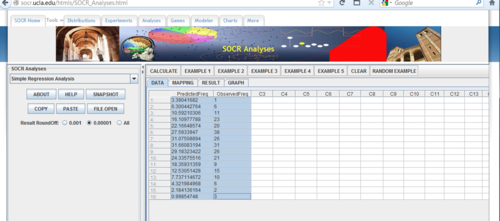
SOCR Activity BMI ChiSquare Fig12.png

Map the predicted and observed frequencies to the Dependent and Independent variables (Mapping Tab).

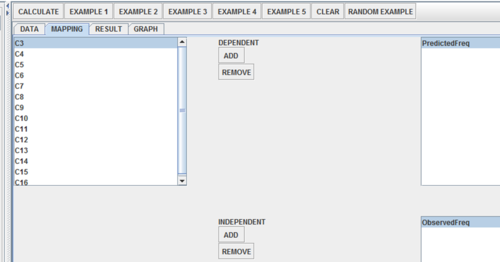
SOCR Activity BMI ChiSquare Fig13.png

Click Calculate button to view the results. Regression Model:

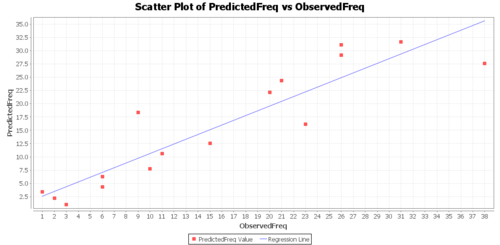
PredictedFreq = 1.71070 + 0.8918062570205698 * ObservedFreq
Correlation(ObservedFreq, PredictedFreq) = .91394
R-Square = .83529
Intercept:
Parameter Estimate: 1.71070
Standard Error: 2.00468
T-Statistics: .85335
P-Value: .40783
Slope:
Parameter Estimate: .89181
Standard Error: .10584
T-Statistics: 8.42598
P-Value: .00000

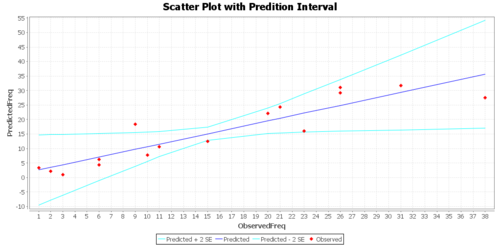
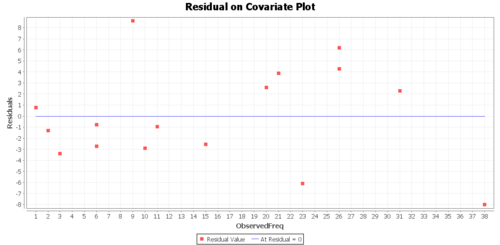
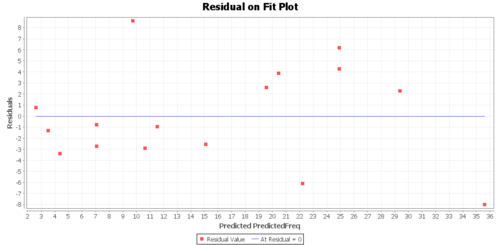
Regression Graphs

The Graphs tab includes a regression model plot, scatter plot with confidence/prediction limits, and various plots of the residuals.

SOCR Activity BMI ChiSquare Fig14.png
SOCR Activity BMI ChiSquare Fig15.png
SOCR Activity BMI ChiSquare Fig16.png
SOCR Activity BMI ChiSquare Fig17.png
SOCR Activity BMI ChiSquare Fig18.png

Practice problems

  • Try this method out on one of the other variables. See if it breaks from the normal distribution.
  • Many biological measures are said to follow a normal distribution. Look under the data header “Biomedical Data” in the SOCR Free Datasets and check this claim out with one of the variables you are interested in.

See also

References

Translate this page:

(default)
Uk flag.gif

Deutsch
De flag.gif

Español
Es flag.gif

Français
Fr flag.gif

Italiano
It flag.gif

Português
Pt flag.gif

日本語
Jp flag.gif

България
Bg flag.gif

الامارات العربية المتحدة
Ae flag.gif

Suomi
Fi flag.gif

इस भाषा में
In flag.gif

Norge
No flag.png

한국어
Kr flag.gif

中文
Cn flag.gif

繁体中文
Cn flag.gif

Русский
Ru flag.gif

Nederlands
Nl flag.gif

Ελληνικά
Gr flag.gif

Hrvatska
Hr flag.gif

Česká republika
Cz flag.gif

Danmark
Dk flag.gif

Polska
Pl flag.png

România
Ro flag.png

Sverige
Se flag.gif

Retrieved from "https://wiki.socr.umich.edu/index.php?title=SOCR_EduMaterials_Activities_BMI_Modeling_Activity&oldid=12607"