Difference between revisions of "SMHS TimeSeriesAnalysis"
(→Scientific Methods for Health Sciences - Time Series Analysis) |
(→Scientific Methods for Health Sciences - Time Series Analysis) |
||
| Line 23: | Line 23: | ||
<b>par</b>(mfrow=c(3,2)) | <b>par</b>(mfrow=c(3,2)) | ||
| − | n <- 98 | + | <b>n <- 98</b> |
X <- cbind(1:n) # time points (annually) | X <- cbind(1:n) # time points (annually) | ||
| − | Trend1 <- LakeHuron+0.2*X # series 1 | + | <u>Trend1</u> <- LakeHuron+0.2*X # series 1 |
Trend2 <- LakeHuron-0.5*X # series 2 | Trend2 <- LakeHuron-0.5*X # series 2 | ||
| + | |||
| + | <u>Season1</u> <- X; Season2 <- X; # series 1 & 2 | ||
| + | for(i in 1:n) { | ||
| + | <b>Season1</b>[i] <- LakeHuron[i] + 5*(i%%4) | ||
| + | <b>Season2</b>[i] <- LakeHuron[i] -2*(i%%10) | ||
| + | } | ||
Revision as of 13:11, 5 May 2016
Scientific Methods for Health Sciences - Time Series Analysis
Questions
• Why are trends, patterns or predictions from models/data important?
• How to detect, model and utilize trends in longitudinal data?
Time series analysis represents a class of statistical methods applicable for series data aiming to extract meaningful information, trend and characterization of the process using observed longitudinal data. These trends may be used for time series forecasting and for prediction of future values based on retrospective observations. Note that classical linear modeling (e.g., regression analysis) may also be employed for prediction & testing of associations using the values of one or more independent variables and their affect the value of another variable. However, time series analysis allows dependencies (e.g., seasonal effects to be accounted for).
Time-series representation
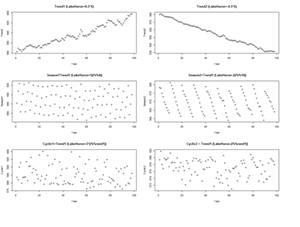
There are 3 (distinct and complementary) types of time series patterns that most time-series analyses are trying to identify, model and analyze. These include:
• Trend: A trend is a long-term increase or decrease in the data that may be linear or non-linear, but is generally continuous (mostly monotonic). The trend may be referred to as direction.
• Seasonal: A seasonal pattern is influence in the data, like seasonal factors (e.g., the quarter of the year, the month, or day of the week), which is always of a fixed known period.
• Cyclic: A cyclic pattern of fluctuations corresponds to rises and falls that are not of fixed period.
For example, the following code shows several time series with different types of time series patterns.
par(mfrow=c(3,2))
n <- 98 X <- cbind(1:n) # time points (annually) Trend1 <- LakeHuron+0.2*X # series 1 Trend2 <- LakeHuron-0.5*X # series 2
Season1 <- X; Season2 <- X; # series 1 & 2
for(i in 1:n) {
Season1[i] <- LakeHuron[i] + 5*(i%%4)
Season2[i] <- LakeHuron[i] -2*(i%%10)
}