Difference between revisions of "SMHS BigDataBigSci CrossVal"
(→Example (Linear Regression)) |
(→See also) |
||
| (35 intermediate revisions by 2 users not shown) | |||
| Line 5: | Line 5: | ||
* Can we do “pretend” validations that closely mimic reality? | * Can we do “pretend” validations that closely mimic reality? | ||
| − | [[Image:SMHS_BigDataBigSci_CrossVal1.png|250px]] | + | <center>[[Image:SMHS_BigDataBigSci_CrossVal1.png|250px]]</center> |
''Validation'' is the scientific process of determining the degree of accuracy of a mathematical, analytic or computational model as a representation of the real world based on the intended model use. There are various challenges with using observed experimental data for model validation: | ''Validation'' is the scientific process of determining the degree of accuracy of a mathematical, analytic or computational model as a representation of the real world based on the intended model use. There are various challenges with using observed experimental data for model validation: | ||
| Line 17: | Line 17: | ||
==Overview== | ==Overview== | ||
| − | ==Cross-validation== | + | ====Cross-validation==== |
Cross-validation is a method for validating of models by assessing the reliability and stability of the results of a statistical analysis (e.g., model predictions) based on independent datasets. For prediction of trend, association, clustering, etc., a model is usually trained on one dataset (training data) and tested on new unknown data (testing dataset). The cross-validation method defines a test dataset to evaluate the model avoiding overfitting (the process when a computational model describes random error, or noise, instead of underlying relationships in the data). | Cross-validation is a method for validating of models by assessing the reliability and stability of the results of a statistical analysis (e.g., model predictions) based on independent datasets. For prediction of trend, association, clustering, etc., a model is usually trained on one dataset (training data) and tested on new unknown data (testing dataset). The cross-validation method defines a test dataset to evaluate the model avoiding overfitting (the process when a computational model describes random error, or noise, instead of underlying relationships in the data). | ||
| − | ==Overfitting== | + | ====Overfitting==== |
'''Example (US Presidential Elections):''' By 2014, there have been only '''56 presidential elections and 43 presidents'''. That is a small dataset, and learning from it may be challenging. <u>'''If the predictor space expands to include things like having false teeth, it's pretty easy for the model to go from fitting the generalizable features of the data (the signal) and to start matching the noise.'''</u> When this happens, the quality of the fit on the historical data may improve (e.g., better R<sup>2</sup>), but the model may fail miserably when used to make inferences about future presidential elections. | '''Example (US Presidential Elections):''' By 2014, there have been only '''56 presidential elections and 43 presidents'''. That is a small dataset, and learning from it may be challenging. <u>'''If the predictor space expands to include things like having false teeth, it's pretty easy for the model to go from fitting the generalizable features of the data (the signal) and to start matching the noise.'''</u> When this happens, the quality of the fit on the historical data may improve (e.g., better R<sup>2</sup>), but the model may fail miserably when used to make inferences about future presidential elections. | ||
| Line 27: | Line 27: | ||
(Figure from http://xkcd.com/1122/) | (Figure from http://xkcd.com/1122/) | ||
| − | [[Image:SMHS BigDataBigSci_CrossVal2.png|400px]] | + | <center>[[Image:SMHS BigDataBigSci_CrossVal2.png|400px]]</center> |
'''Example (Google Flu Trends):''' A March 14, 2014 article in Science (''DOI: 10.1126/science.1248506''), identified problems in Google Flu Trends (http://www.google.org/flutrends/about/#US), DOI 10.1371/journal.pone.0023610, which may be attributed in part to overfitting. In February 2013, Nature reported that GFT was predicting more than double the proportion of doctor visits for influenza-like illness (ILI) than the Centers for Disease Control and Prevention (CDC), despite the fact that GFT was built to predict CDC reports. | '''Example (Google Flu Trends):''' A March 14, 2014 article in Science (''DOI: 10.1126/science.1248506''), identified problems in Google Flu Trends (http://www.google.org/flutrends/about/#US), DOI 10.1371/journal.pone.0023610, which may be attributed in part to overfitting. In February 2013, Nature reported that GFT was predicting more than double the proportion of doctor visits for influenza-like illness (ILI) than the Centers for Disease Control and Prevention (CDC), despite the fact that GFT was built to predict CDC reports. | ||
| Line 43: | Line 43: | ||
'''Cross-validation is an iterative process''', where each step involves: | '''Cross-validation is an iterative process''', where each step involves: | ||
| − | + | *Randomly partitioning a sample of data into 2 complementary subsets (training + testing), | |
| − | + | *Performing the analysis on the training subset | |
| − | + | *Validating the analysis on the testing subset | |
| − | + | *Increase the iteration index and repeat the process (termination criteria can involve a fixed number, or a desired (mean?) variability or error-rate). | |
| − | [[Image:SMHS BigDataBigSci_CrossVal3.png|400px]] | + | <center>[[Image:SMHS BigDataBigSci_CrossVal3.png|400px]]</center> |
The validation results at each iteration are averaged, to reduce noise/variability, and reported. | The validation results at each iteration are averaged, to reduce noise/variability, and reported. | ||
| − | Cross-validation guards against testing hypotheses suggested by the data themselves (aka | + | Cross-validation guards against testing hypotheses suggested by the data themselves (aka: "Type III errors", False-Suggestion) in cases when new observations are hard to obtain (due to costs, reliability, time or other constraints). |
Cross-validation is different from ''conventional-validation'' (e.g. 80%-20% partitioning the data set into training and testing subsets) as the in the conventional validation, the error (e.g. Root Mean Square Error, RMSE) on the training data is not a useful estimator of model performance, as it does not generalize across multiple samples. Errors of the conventional-valuation based on the results on the test data do not assess model performance, in general. A more fair way to properly estimate model prediction performance is to use cross-validation, which combines (averages) prediction errors or measures of fit to correct for the stochastic nature of training and testing data partitions and generate a more accurate and robust estimate of real model performance. | Cross-validation is different from ''conventional-validation'' (e.g. 80%-20% partitioning the data set into training and testing subsets) as the in the conventional validation, the error (e.g. Root Mean Square Error, RMSE) on the training data is not a useful estimator of model performance, as it does not generalize across multiple samples. Errors of the conventional-valuation based on the results on the test data do not assess model performance, in general. A more fair way to properly estimate model prediction performance is to use cross-validation, which combines (averages) prediction errors or measures of fit to correct for the stochastic nature of training and testing data partitions and generate a more accurate and robust estimate of real model performance. | ||
| Line 61: | Line 61: | ||
A more complex model ''overfits-the-data'', relative to a simpler model when the former generates accurate fitting results for known data but less accurate results when predicting based on new data (foresight). Knowledge from past experience includes information either ''relevant or irrelevant'' (noise) for the future information. In challenging data-driven predict models when uncertainty (entropy) is high, more noise is present in past information that needs to be ignored in future forecasting. However it is generally hard to discriminate patterns from noise in complex systems (i.e., deciding which part to model and which to ignore). Models that reduce the chance of fitting noise are called '''robust'''. | A more complex model ''overfits-the-data'', relative to a simpler model when the former generates accurate fitting results for known data but less accurate results when predicting based on new data (foresight). Knowledge from past experience includes information either ''relevant or irrelevant'' (noise) for the future information. In challenging data-driven predict models when uncertainty (entropy) is high, more noise is present in past information that needs to be ignored in future forecasting. However it is generally hard to discriminate patterns from noise in complex systems (i.e., deciding which part to model and which to ignore). Models that reduce the chance of fitting noise are called '''robust'''. | ||
| − | ==Example (Linear Regression)== | + | ====Example (Linear Regression)==== |
| − | We can demonstrate model assessment using linear regression. Suppose we observe response values ${y_1,...,y_n}$, and the corresponding $k$ predictors represented as a $kD$ vector of covariates ${x_1,...,x_n}$, where subjects/cases are indexed by $1 ≤ i ≤ n$, and the data-elements (variables) are indexed by $1 ≤ j ≤ k$. | + | We can demonstrate model assessment using linear regression. Suppose we observe response values $\{y_1,...,y_n\}$, and the corresponding $k$ predictors represented as a $kD$ vector of covariates $\{x_1,...,x_n\}$, where subjects/cases are indexed by $1 ≤ i ≤ n$, and the data-elements (variables) are indexed by $1 ≤ j ≤ k$. |
\begin{pmatrix} | \begin{pmatrix} | ||
| Line 71: | Line 71: | ||
\end{pmatrix} | \end{pmatrix} | ||
| − | + | Using least squares to estimate the linear function parameters (effect-sizes), $\{β_1,...,β_k\}$, allows us to compute a hyperplane $y = a + xβ$ that best fits the observed data $\{x_i,y_i\}_{1≤i≤n}$. | |
| − | |||
| − | Using least squares to estimate the linear function parameters (effect-sizes), ${β_1,...,β_k}$, allows us to compute a hyperplane $y = a + xβ$ that best fits the observed data | ||
| − | |||
| − | |||
\begin{equation} | \begin{equation} | ||
| Line 104: | Line 100: | ||
| + | $$ | ||
| + | \begin{array}{lcl} | ||
| + | y_1=\alpha_1+x_{1,1}\beta_1+x_{1,2}\beta_2+...+x_{1,k}\beta_k\\ | ||
| + | y_2=\alpha_2+x_{2,1}\beta_1+x_{2,2}\beta_2+...+x_{2,k}\beta_k \\ | ||
| + | ...\\ | ||
| + | y_n=\alpha_n+x_{n,1}\beta_1+x_{n,2}\beta_2+...+x_{n,k}\beta_k | ||
| + | \end{array}$$ | ||
| + | The model fit may be evaluated using the mean squared error (MSE). The MSE for a given value of the parameters ''α'' and ''β'' on the observed training data $\{x_i,y_i\}_{1 ≤ i ≤ n}$. | ||
| − | + | $$ | |
| − | + | \begin{equation} MSE=\frac{1}{n}\sum_{i=1}^{n} \Bigg(y_i-\underbrace{(\alpha_1+x_{i,1}\beta_1+x_{i,2}\beta_2+\cdots+x_{i,k}\beta_k)}_{(\text{predicted value, } \hat{y_i} \text{, at }\{x_{i,1,}\cdots,x_{i,k}\})} \Bigg)^2 | |
| − | + | \end{equation} | |
| − | + | $$ | |
| − | + | <center>vs.</center> | |
| − | < | + | $$ |
| − | + | \begin{equation} RMSE=\sqrt{\frac{1}{n}\sum_{i=1}^{n} \Bigg(y_i-\underbrace{(\alpha_1+x_{i,1}\beta_1+x_{i,2}\beta_2+\cdots+x_{i,k}\beta_k)}_{(\text{predicted value, } \hat{y_i} \text{, at }\{x_{i,1,}\cdots,x_{i,k}\})} \Bigg)^2 }. | |
| − | \begin{equation} | ||
\end{equation} | \end{equation} | ||
| + | $$ | ||
| − | + | The expected value of the MSE (over the distribution of training sets) for the <u>'''training set'''</u> is $\frac{(n-k-1)}{(n + k + 1)} × E,$ where $E$ is the expected value of the MSE for the <u>'''testing'''</u>/<u>'''validation'''</u> data. Therefore, fitting a model and computing the MSE on the training set, we will get an over optimistic evaluation assessment (smaller RMSE) of how well the model may fit another dataset. This bias represents ''in-sample'' estimate of the fit, whereas we are interested in the cross-validation estimate as an ''out-of-sample'' estimate. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | The expected value of the MSE (over the distribution of training sets) for the <u>'''training set'''</u> is $\frac{(n - k - 1)}{(n + k + 1)} × E,$ where $E$ is the expected value of the MSE for the <u>'''testing'''</u>/<u>'''validation'''</u> data. Therefore, fitting a model and computing the MSE on the training set, we will get an over optimistic evaluation assessment (smaller RMSE) of how well the model may fit another dataset. This bias represents ''in-sample'' estimate of the fit, whereas we are interested in the cross-validation estimate as an ''out-of-sample'' estimate. | ||
In the linear regression model, cross validation is not useful as we can compute the <u>'''exact'''</u> correction factor $\frac{(n - k - 1)}{(n + k + 1)}$ and correctly estimate the ''out-of-sample'' fit using the (MSE underestimate) ''in-sample'' MSE estimate. However, even in this situation, cross-validation remains useful as it can be used to select an optimal regularized cost function. | In the linear regression model, cross validation is not useful as we can compute the <u>'''exact'''</u> correction factor $\frac{(n - k - 1)}{(n + k + 1)}$ and correctly estimate the ''out-of-sample'' fit using the (MSE underestimate) ''in-sample'' MSE estimate. However, even in this situation, cross-validation remains useful as it can be used to select an optimal regularized cost function. | ||
| Line 128: | Line 126: | ||
In most other modeling procedures (e.g. logistic regression), <u>'''in general'''</u>, there are no simple closed-form expressions (formulas) to adjust the cross-validation error estimate from the in-sample fit estimate. Cross-validation is generally applicable way to predict the performance of a model on a validation set using stochastic computation instead of obtaining experimental, theoretical, mathematical, or analytic error estimates. | In most other modeling procedures (e.g. logistic regression), <u>'''in general'''</u>, there are no simple closed-form expressions (formulas) to adjust the cross-validation error estimate from the in-sample fit estimate. Cross-validation is generally applicable way to predict the performance of a model on a validation set using stochastic computation instead of obtaining experimental, theoretical, mathematical, or analytic error estimates. | ||
| − | ==Cross-validation methods== | + | ====Cross-validation methods==== |
There are 2 classes of cross-validation approaches – exhaustive and non-exhaustive. | There are 2 classes of cross-validation approaches – exhaustive and non-exhaustive. | ||
| Line 138: | Line 136: | ||
'''Non-exhaustive cross-validation''' | '''Non-exhaustive cross-validation''' | ||
| − | Non-exhaustive cross validation methods avoid computing estimates/errors using all possible partitionings of the original sample, but rather approximates these. For example, in the '''''k''-fold cross-validation''', the original sample is randomly partitioned into $k$ equal sized subsamples. Of the $k$ subsamples, a single subsample is kept as final testing data for validation of the model. The other $k- 1$ subsamples are used as training data. The cross-validation process is then repeated $k$ times ($k$ folds). Each of the $k$ subsamples is used once as the validation data. There are corresponding $k$ results that are averaged (or otherwise aggregated) to generate a final model-quality estimation. In $k$-fold validation, all observations are used for both training and validation, and each observation is used for validation exactly once. In general, $k$ is a parameter that needs to be selected by investigator (common values may be 5, 10). | + | Non-exhaustive cross validation methods avoid computing estimates/errors using all possible partitionings of the original sample, but rather approximates these. For example, in the <u>'''''k''-fold cross-validation'''</u>, the original sample is randomly partitioned into $k$ equal sized subsamples. Of the $k$ subsamples, a single subsample is kept as final testing data for validation of the model. The other $k- 1$ subsamples are used as training data. The cross-validation process is then repeated $k$ times ($k$ folds). Each of the $k$ subsamples is used once as the validation data. There are corresponding $k$ results that are averaged (or otherwise aggregated) to generate a final model-quality estimation. In $k$-fold validation, all observations are used for both training and validation, and each observation is used for validation exactly once. In general, $k$ is a parameter that needs to be selected by investigator (common values may be 5, 10). |
A general case of the $k$-fold validation is $k=n$ (the total number of observations), when it coincides with the '''leave-one-out cross-validation'''. | A general case of the $k$-fold validation is $k=n$ (the total number of observations), when it coincides with the '''leave-one-out cross-validation'''. | ||
| − | |||
A variation of the $k$-fold validation is <u>'''stratified k-fold cross-validation'''</u>, where each fold has the same (approximately) mean response value. For instance, if the model represents a binary classification of cases (e.g., NC vs. PD), this implies that each fold contains roughly the same proportion of the 2 class labels. | A variation of the $k$-fold validation is <u>'''stratified k-fold cross-validation'''</u>, where each fold has the same (approximately) mean response value. For instance, if the model represents a binary classification of cases (e.g., NC vs. PD), this implies that each fold contains roughly the same proportion of the 2 class labels. | ||
| − | '''Repeated random sub-sampling validation''' splits randomly the entire dataset into training (where the model is fit) and testing data where the predictive accuracy is assessed). Again, the results are averaged over all iterative splits. This method has an advantage over | + | '''Repeated random sub-sampling validation''' splits randomly the entire dataset into training (where the model is fit) and testing data where the predictive accuracy is assessed). Again, the results are averaged over all iterative splits. This method has an advantage over $k$-fold cross validation as that the proportion of the training/testing split is not dependent on the number of iterations (folds). However, its drawback is that some observations may never be selected whereas others may be selected multiple-times in the testing/validation subsample, as validation subsets may overlap, and the results will vary each time we repeat the validation protocol (unless we set a seed point in the algorithm). |
Asymptotically, as the number of random splits increases, the ''repeated random sub-sampling validation'' approaches the ''leave-k-out cross-validation''. | Asymptotically, as the number of random splits increases, the ''repeated random sub-sampling validation'' approaches the ''leave-k-out cross-validation''. | ||
| − | ==Case-Studies== | + | ====Case-Studies==== |
'''Example 1: Parkinson’s Diseases Study''' involving neuroimaging, genetics, clinical, and phenotypic data for over 600 volunteers produced multivariate data for 3 cohorts (HC=Healthy Controls, PD=Parkinson’s, SWEDD= subjects without evidence for dopaminergic deficit). | '''Example 1: Parkinson’s Diseases Study''' involving neuroimaging, genetics, clinical, and phenotypic data for over 600 volunteers produced multivariate data for 3 cohorts (HC=Healthy Controls, PD=Parkinson’s, SWEDD= subjects without evidence for dopaminergic deficit). | ||
| − | # update packages | + | # update packages |
# update.packages() | # update.packages() | ||
| − | + | ||
| − | #load the data: 06_PPMI_ClassificationValidationData_Short.csv | + | #load the data: 06_PPMI_ClassificationValidationData_Short.csv |
ppmi_data <-read.csv("https://umich.instructure.com/files/330400/download?download_frd=1",header=TRUE) | ppmi_data <-read.csv("https://umich.instructure.com/files/330400/download?download_frd=1",header=TRUE) | ||
| − | + | ||
| − | #binarize the Dx classes | + | #binarize the Dx classes |
ppmi_data$\$$ResearchGroup <- ifelse(ppmi_data$\$$ResearchGroup == "Control", "Control", "Patient") | ppmi_data$\$$ResearchGroup <- ifelse(ppmi_data$\$$ResearchGroup == "Control", "Control", "Patient") | ||
attach(ppmi_data) | attach(ppmi_data) | ||
| − | + | ||
head(ppmi_data) | head(ppmi_data) | ||
| − | # Model-free analysis, classification | + | # Model-free analysis, classification |
# install.packages("crossval") | # install.packages("crossval") | ||
#library("crossval") | #library("crossval") | ||
| Line 172: | Line 169: | ||
require(ada) | require(ada) | ||
#set up adaboosting prediction function | #set up adaboosting prediction function | ||
| + | |||
| − | #Define a new classification result-reporting function | + | #Define a new classification result-reporting function |
my.ada <- function (train.x, train.y, test.x, test.y, negative, formula){ | my.ada <- function (train.x, train.y, test.x, test.y, negative, formula){ | ||
ada.fit <- ada(train.x, train.y) | ada.fit <- ada(train.x, train.y) | ||
| Line 182: | Line 180: | ||
return (out) | return (out) | ||
} | } | ||
| − | + | ||
| − | #balance cases | + | #balance cases |
#SMOTE: Synthetic Minority Oversampling Technique to handle class misbalance in binary classification. | #SMOTE: Synthetic Minority Oversampling Technique to handle class misbalance in binary classification. | ||
set.seed(1000) | set.seed(1000) | ||
| Line 192: | Line 190: | ||
ppmi_data <- ppmi_data[ppmi_data$\$$VisitID==1,] | ppmi_data <- ppmi_data[ppmi_data$\$$VisitID==1,] | ||
'''ppmi_data$\$$PD <- factor(ppmi_data$\$$PD)''' | '''ppmi_data$\$$PD <- factor(ppmi_data$\$$PD)''' | ||
| − | + | ||
colnames(ppmi_data) | colnames(ppmi_data) | ||
#ppmi_data.1<-ppmi_data[,c(3:281,284,287,336:340,341)] | #ppmi_data.1<-ppmi_data[,c(3:281,284,287,336:340,341)] | ||
n <- ncol(ppmi_data) | n <- ncol(ppmi_data) | ||
output.1 <- ppmi_data$\$$PD | output.1 <- ppmi_data$\$$PD | ||
| − | + | ||
| − | # remove Default Real Clinical subject classifications! | + | # remove Default Real Clinical subject classifications! |
ppmi_data$\$$PD <- ifelse(ppmi_data$\$$ResearchGroup=="Control",1,0) | ppmi_data$\$$PD <- ifelse(ppmi_data$\$$ResearchGroup=="Control",1,0) | ||
input <- ppmi_data[ ,-which(names(ppmi_data) %in% c("ResearchGroup","PD", "X", "FID_IID"))] | input <- ppmi_data[ ,-which(names(ppmi_data) %in% c("ResearchGroup","PD", "X", "FID_IID"))] | ||
| Line 204: | Line 202: | ||
output <- as.factor(ppmi_data$\$$PD) | output <- as.factor(ppmi_data$\$$PD) | ||
c(dim(input), dim(output)) | c(dim(input), dim(output)) | ||
| − | + | ||
| − | # balance the dataset | + | # balance the dataset |
data.1<-ubBalance(X= input, Y=output, type="ubSMOTE", percOver=300, percUnder=150, verbose=TRUE) | data.1<-ubBalance(X= input, Y=output, type="ubSMOTE", percOver=300, percUnder=150, verbose=TRUE) | ||
balancedData<-cbind(data.1$\$$X, data.1$\$$Y) | balancedData<-cbind(data.1$\$$X, data.1$\$$Y) | ||
| Line 211: | Line 209: | ||
nrow(balancedData); ncol(balancedData) | nrow(balancedData); ncol(balancedData) | ||
nrow(input); ncol(input) | nrow(input); ncol(input) | ||
| − | + | ||
colnames(balancedData) <- c(colnames(input), "PD") | colnames(balancedData) <- c(colnames(input), "PD") | ||
| − | + | ||
| − | ###Check balance | + | ###Check balance |
##T test | ##T test | ||
alpha.0.05 <- 0.05 | alpha.0.05 <- 0.05 | ||
test.results.bin <- NULL # binarized/dichotomized p-values | test.results.bin <- NULL # binarized/dichotomized p-values | ||
test.results.raw <- NULL # raw p-values | test.results.raw <- NULL # raw p-values | ||
| − | + | ||
| − | # get a better error-handling t.test function that gracefully handles NA’s and trivial variances | + | # get a better error-handling t.test function that gracefully handles NA’s and trivial variances |
my.t.test.p.value <- function(input1, input2) { | my.t.test.p.value <- function(input1, input2) { | ||
obj <- try(t.test(input1, input2), silent=TRUE) | obj <- try(t.test(input1, input2), silent=TRUE) | ||
| − | if (is(obj, "try-error")) return(NA) else return(obj$\$$p.value) | + | if (is(obj, "try-error")) return(NA) else return('''obj$\$$p.value''') |
} | } | ||
| + | |||
| + | |||
for (i in 1:ncol(balancedData)) | for (i in 1:ncol(balancedData)) | ||
{ | { | ||
| Line 239: | Line 239: | ||
#sum(test.results.raw < alpha.0.05, na.rm=T)/length(test.results.raw) #check proportion of inconsistencies | #sum(test.results.raw < alpha.0.05, na.rm=T)/length(test.results.raw) #check proportion of inconsistencies | ||
#sum(test.results.corr < alpha.0.05, na.rm =T)/length(test.results.corr) | #sum(test.results.corr < alpha.0.05, na.rm =T)/length(test.results.corr) | ||
| + | |||
| − | #as the sample-size is changed: | + | #as the sample-size is changed: |
length(input[,5]); length(balancedData [,5]) | length(input[,5]); length(balancedData [,5]) | ||
#to plot raw vs. rebalanced pairs (e.g., var="L_insular_cortex_Volume"), we need to equalize the lengths | #to plot raw vs. rebalanced pairs (e.g., var="L_insular_cortex_Volume"), we need to equalize the lengths | ||
plot (input[,5] +0*balancedData [,5], balancedData [,5]) # [,5] == "L_insular_cortex_Volume" | plot (input[,5] +0*balancedData [,5], balancedData [,5]) # [,5] == "L_insular_cortex_Volume" | ||
| − | + | ||
print(c("T-test results: ", test.results)) | print(c("T-test results: ", test.results)) | ||
#zeros (0) are significant independent between-group T-test differences, ones (1) are insignificant | #zeros (0) are significant independent between-group T-test differences, ones (1) are insignificant | ||
| − | + | ||
for (i in 1:(ncol(balancedData)-1)) | for (i in 1:(ncol(balancedData)-1)) | ||
{ | { | ||
| Line 269: | Line 270: | ||
#'''Side note''': There is a function name collision for “crossval”, the same method is present in | #'''Side note''': There is a function name collision for “crossval”, the same method is present in | ||
| − | + | ||
| − | + | #the “'''mlr'''” (machine Learning in R) package and in the “'''crossval'''” package. | |
| + | |||
| + | #To specify a function call from a specific package do: packagename::functionname() | ||
set.seed(115) | set.seed(115) | ||
| Line 315: | Line 318: | ||
levels(Y) # "1" "2" | levels(Y) # "1" "2" | ||
dim(X) # 20 1 | dim(X) # 20 1 | ||
| − | + | ||
set.seed(123456) | set.seed(123456) | ||
cv.out <- '''crossval::crossval'''(predfun.lda, X, Y, K=5, B=20, negative="1") | cv.out <- '''crossval::crossval'''(predfun.lda, X, Y, K=5, B=20, negative="1") | ||
| Line 323: | Line 326: | ||
'''(2) A model-based example (linear regression) using the attitude dataset:''' | '''(2) A model-based example (linear regression) using the attitude dataset:''' | ||
| − | #?attitude, colnames(attitude) | + | '''#?attitude, colnames(attitude)''' |
#"rating" "complaints" "privileges" "learning" "raises" "critical" "advance" | #"rating" "complaints" "privileges" "learning" "raises" "critical" "advance" | ||
| Line 339: | Line 342: | ||
data("attitude") | data("attitude") | ||
y = attitude[,1] # rating variable | y = attitude[,1] # rating variable | ||
| − | x = attitude[,-1] | + | x = attitude[,-1] # date frame with the remaining variables |
is.factor(y) | is.factor(y) | ||
summary( lm(y ~ . , data=x) ) # R-squared: 0.7326 | summary( lm(y ~ . , data=x) ) # R-squared: 0.7326 | ||
#set up lm prediction function | #set up lm prediction function | ||
| + | |||
'''predfun.lm = function(train.x, train.y, test.x, test.y)''' | '''predfun.lm = function(train.x, train.y, test.x, test.y)''' | ||
| Line 354: | Line 358: | ||
return(out) | return(out) | ||
} | } | ||
| − | + | ||
| − | + | #require("MASS") | |
| − | #require("MASS") | + | |
| − | |||
'''predfun.lda = function(train.x, train.y, test.x, test.y, negative)''' | '''predfun.lda = function(train.x, train.y, test.x, test.y, negative)''' | ||
{ lda.fit = lda(train.x, grouping=train.y) | { lda.fit = lda(train.x, grouping=train.y) | ||
| − | + | ynew = predict(lda.fit, test.x)$\$$class | |
| − | + | #count TP, FP etc. | |
| − | + | out = confusionMatrix(test.y, ynew, negative=negative) | |
| − | + | return( out ) | |
} | } | ||
| − | + | ||
| − | #prediction MSE using all variables | + | #prediction MSE using all variables |
| − | |||
set.seed(123456) | set.seed(123456) | ||
cv.out.lm = '''crossval::crossval'''(predfun.lm, x, y, K=5, B=20, negative="1") | cv.out.lm = '''crossval::crossval'''(predfun.lm, x, y, K=5, B=20, negative="1") | ||
| Line 386: | Line 388: | ||
#input <- ppmi_data[ ,-which(names(ppmi_data) %in% c("ResearchGroup","PD", "X", "FID_IID"))] | #input <- ppmi_data[ ,-which(names(ppmi_data) %in% c("ResearchGroup","PD", "X", "FID_IID"))] | ||
#output <- as.factor(ppmi_data$\$$PD) | #output <- as.factor(ppmi_data$\$$PD) | ||
| − | + | ||
| − | #remove the irrelevant variables (e.g., visit ID) | + | #remove the irrelevant variables (e.g., visit ID) |
| − | |||
output <- as.factor(ppmi_data$\$$PD) | output <- as.factor(ppmi_data$\$$PD) | ||
input <- ppmi_data[, -which(names(ppmi_data) %in% c("ResearchGroup","PD", "X", "FID_IID", "VisitID"))] | input <- ppmi_data[, -which(names(ppmi_data) %in% c("ResearchGroup","PD", "X", "FID_IID", "VisitID"))] | ||
| Line 394: | Line 395: | ||
Y = as.matrix(output) # Actual PD clinical assessment | Y = as.matrix(output) # Actual PD clinical assessment | ||
dim(X); dim(Y) | dim(X); dim(Y) | ||
| − | + | ||
layout(matrix(c(1,2,3,4),2,2)) # optional 4 graphs/page | layout(matrix(c(1,2,3,4),2,2)) # optional 4 graphs/page | ||
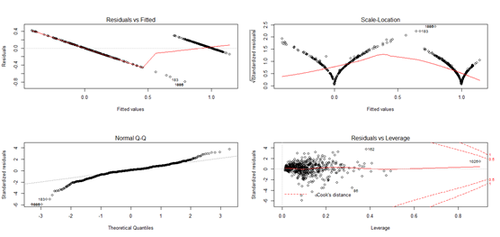
fit <- lm(Y~X); plot(fit) # plot the fit | fit <- lm(Y~X); plot(fit) # plot the fit | ||
levels(as.factor(Y)) # "0" "1" | levels(as.factor(Y)) # "0" "1" | ||
c(dim(X), dim(Y)) # 1043 103 | c(dim(X), dim(Y)) # 1043 103 | ||
| − | + | ||
set.seed(12345) | set.seed(12345) | ||
#cv.out.lm = '''crossval::crossval'''(predfun.lm, as.data.frame(X), as.numeric(Y), K=5, B=20) | #cv.out.lm = '''crossval::crossval'''(predfun.lm, as.data.frame(X), as.numeric(Y), K=5, B=20) | ||
| − | + | ||
cv.out.lda = crossval::crossval(predfun.lda, X, Y, K=5, B=20, negative="1") | cv.out.lda = crossval::crossval(predfun.lda, X, Y, K=5, B=20, negative="1") | ||
#K=Number of folds; <u>'''B=Number of repetitions.'''</u> | #K=Number of folds; <u>'''B=Number of repetitions.'''</u> | ||
| − | + | ||
| − | #Results | + | #Results |
| − | + | ||
cv.out.lda$\$$stat; cv.out.lda; diagnosticErrors(cv.out.lda$\$$stat) | cv.out.lda$\$$stat; cv.out.lda; diagnosticErrors(cv.out.lda$\$$stat) | ||
cv.out.lm$\$$stat; cv.out.lm; diagnosticErrors(cv.out.lm$\$$stat) | cv.out.lm$\$$stat; cv.out.lm; diagnosticErrors(cv.out.lm$\$$stat) | ||
| Line 414: | Line 415: | ||
'''The cross-validation (CV) output object includes the following components:''' | '''The cross-validation (CV) output object includes the following components:''' | ||
| − | + | *stat.cv: ''Vector'' od statistics returned by predfun for each cross validation run | |
| − | + | *stat: ''Mean'' the statistic returned by predfun averaged over all cross validation runs | |
| − | + | *stat.se: ''Variability'': the corresponding standard error. | |
| Line 437: | Line 438: | ||
[[Image:SMHS_BigDataBigSci_CrossVal4.png|500px]] | [[Image:SMHS_BigDataBigSci_CrossVal4.png|500px]] | ||
| − | ==Alternative predictor functions== | + | ====Alternative predictor functions==== |
<b>Logistic Regression</b> | <b>Logistic Regression</b> | ||
| Line 463: | Line 464: | ||
ynew <- predict(lm.logit, as.data.frame(X)); plot(ynew) | ynew <- predict(lm.logit, as.data.frame(X)); plot(ynew) | ||
ynew2 <- ifelse(exp(ynew)<0.5, 0, 1); plot(ynew2) | ynew2 <- ifelse(exp(ynew)<0.5, 0, 1); plot(ynew2) | ||
| − | + | ||
'''predfun.logit = function(train.x, train.y, test.x, test.y, neg)''' | '''predfun.logit = function(train.x, train.y, test.x, test.y, neg)''' | ||
| − | { lm.logit <- glm(train.y ~ ., data = train.x, family = "binomial") | + | { lm.logit <- glm(train.y ~ ., data = train.x, family = "binomial") |
| − | + | ynew = predict(lm.logit, test.x ) | |
| − | + | #compute TP, FP, TN, FN | |
| − | + | <span style="background-color: #32cd32">ynew2</span> <- ifelse(exp(ynew)<0.5, 0, 1) | |
| − | + | out = confusionMatrix(test.y, ynew2, negative=neg) # Binary outcome, we can use confusionMatrix | |
| − | + | return( out ) | |
} | } | ||
| Line 476: | Line 477: | ||
input.short <- input[, which(names(input) %in% c("R_fusiform_gyrus_Volume", | input.short <- input[, which(names(input) %in% c("R_fusiform_gyrus_Volume", | ||
| − | + | "R_fusiform_gyrus_ShapeIndex", "R_fusiform_gyrus_Curvedness", | |
| − | + | "Sex", "Weight", "Age" , "chr12_rs34637584_GT", "chr17_rs11868035_GT", | |
| − | + | "UPDRS_Part_I_Summary_Score_Baseline", "UPDRS_Part_I_Summary_Score_Month_03", | |
| − | + | "UPDRS_Part_II_Patient_Questionnaire_Summary_Score_Baseline", | |
| − | + | "UPDRS_Part_III_Summary_Score_Baseline", | |
| − | + | "X_Assessment_Non.Motor_Epworth_Sleepiness_Scale_Summary_Score_Baseline" | |
))] | ))] | ||
X = as.matrix(input.short) | X = as.matrix(input.short) | ||
| Line 500: | Line 501: | ||
return( out.qda ) | return( out.qda ) | ||
} | } | ||
| − | + | ||
| − | <mark>cv.out.qda = crossval::crossval(predfun.qda,</mark> as.data.frame(input.short), <mark>as.factor(Y), K=5, B=20, neg="1")</mark> | + | <mark>cv.out.qda = '''crossval::crossval'''(predfun.qda,</mark> as.data.frame(input.short), <mark>as.factor(Y), K=5, B=20, neg="1")</mark> |
| − | |||
diagnosticErrors(cv.out.lda$\$$stat); diagnosticErrors(cv.out.qda$\$$stat); | diagnosticErrors(cv.out.lda$\$$stat); diagnosticErrors(cv.out.qda$\$$stat); | ||
| Line 510: | Line 510: | ||
input.short2 <- input[, which(names(input) %in%)"R_fusiform_gyrus_Volume", | input.short2 <- input[, which(names(input) %in%)"R_fusiform_gyrus_Volume", | ||
| − | + | "Sex", "Weight", "Age" , "chr17_rs11868035_GT", | |
| − | + | "UPDRS_Part_I_Summary_Score_Baseline", | |
| − | + | "UPDRS_Part_II_Patient_Questionnaire_Summary_Score_Baseline", | |
| − | + | "UPDRS_Part_III_Summary_Score_Baseline", | |
| − | + | "X_Assessment_Non.Motor_Epworth_Sleepiness_Scale_Summary_Score_Baseline" | |
| − | + | ))] | |
X = as.matrix(input.short2) | X = as.matrix(input.short2) | ||
cv.out.qda = crossval::crossval(predfun.qda, as.data.frame(X), as.numeric(Y), K=5, B=2, neg="1") | cv.out.qda = crossval::crossval(predfun.qda, as.data.frame(X), as.numeric(Y), K=5, B=2, neg="1") | ||
| Line 522: | Line 522: | ||
diagnosticErrors(cv.out.qda$\$$stat); diagnosticErrors(cv.out.logit$\$$stat) | diagnosticErrors(cv.out.qda$\$$stat); diagnosticErrors(cv.out.logit$\$$stat) | ||
| + | |||
| + | |||
| + | |||
| + | <sup>1</sup>http://www.ohrt.com/odds/binomial.php | ||
==See also== | ==See also== | ||
| Line 527: | Line 531: | ||
* [[SMHS_BigDataBigSci_SEM| Structural Equation Modeling (SEM)]] | * [[SMHS_BigDataBigSci_SEM| Structural Equation Modeling (SEM)]] | ||
* [[SMHS_BigDataBigSci_GCM| Growth Curve Modeling (GCM)]] | * [[SMHS_BigDataBigSci_GCM| Growth Curve Modeling (GCM)]] | ||
| − | * [[ | + | * [[SMHS_BigDataBigSci_GCM| Generalized Estimating Equation (GEE) Modeling]] |
* [[SMHS_BigDataBigSci|Back to Big Data Science]] | * [[SMHS_BigDataBigSci|Back to Big Data Science]] | ||
Latest revision as of 09:08, 24 May 2016
Contents
Big Data Science - (Internal) Statistical Cross-Validaiton
Questions
- What does it mean to validate a result, a method, approach, protocol, or data?
- Can we do “pretend” validations that closely mimic reality?
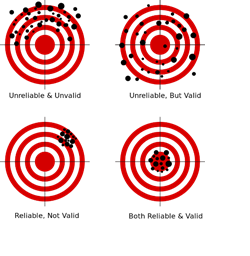
Validation is the scientific process of determining the degree of accuracy of a mathematical, analytic or computational model as a representation of the real world based on the intended model use. There are various challenges with using observed experimental data for model validation:
1. Incomplete details of the experimental conditions may be subject to boundary and initial conditions, sample or material properties, geometry or topology of the system/process.
2. Limited information about measurement errors due to lack of experimental uncertainty estimates.
Empirically observed data may be used to evaluate models with conventional statistical tests applied subsequently to test null hypotheses (e.g., that the model output is correct). In this process, the discrepancy between some model-predicted values and their corresponding/observed counterparts are compared. For example, a regression model predicted values may be compared to empirical observations. Under parametric assumptions of normal residuals and linearity, we could test null hypotheses like $slope = 1$ or $intercept = 0$. When comparing the model obtained on one training dataset to an independent dataset, the slope may be different from 1 and/or the intercept may be different from 0. The purpose of the regression comparison is a formal test of the hypothesis (e.g., $slope = 1, mean_{ observed} =mean_{ predicted},$ then the distributional properties of the adjusted estimates are critical in making an accurate inference. The logistic regression test is another example for comparing predicted and observed values. Measurement errors may creep in, due to sampling or analytical biases, instrument reading or recording errors, temporal or spatial sampling sample collection discrepancies, etc.
Overview
Cross-validation
Cross-validation is a method for validating of models by assessing the reliability and stability of the results of a statistical analysis (e.g., model predictions) based on independent datasets. For prediction of trend, association, clustering, etc., a model is usually trained on one dataset (training data) and tested on new unknown data (testing dataset). The cross-validation method defines a test dataset to evaluate the model avoiding overfitting (the process when a computational model describes random error, or noise, instead of underlying relationships in the data).
Overfitting
Example (US Presidential Elections): By 2014, there have been only 56 presidential elections and 43 presidents. That is a small dataset, and learning from it may be challenging. If the predictor space expands to include things like having false teeth, it's pretty easy for the model to go from fitting the generalizable features of the data (the signal) and to start matching the noise. When this happens, the quality of the fit on the historical data may improve (e.g., better R2), but the model may fail miserably when used to make inferences about future presidential elections.
(Figure from http://xkcd.com/1122/)

Example (Google Flu Trends): A March 14, 2014 article in Science (DOI: 10.1126/science.1248506), identified problems in Google Flu Trends (http://www.google.org/flutrends/about/#US), DOI 10.1371/journal.pone.0023610, which may be attributed in part to overfitting. In February 2013, Nature reported that GFT was predicting more than double the proportion of doctor visits for influenza-like illness (ILI) than the Centers for Disease Control and Prevention (CDC), despite the fact that GFT was built to predict CDC reports.
GFT model found the best matches among 50 million search terms to fit 1,152 data points. The odds of finding search terms that match the propensity of the flu but are structurally unrelated, and so do not predict the future, were quite high. GFT developers, in fact, report weeding out seasonal search terms unrelated to the flu but strongly correlated to the CDC data, e.g., high school basketball season. The big GFT data may have overfitted the small number of cases. The GFT approach missed the non-seasonal 2009 influenza A–H1N1 pandemic.
Example (Autism). Autistic brains constantly overfit visual and cognitive stimuli. To an autistic person, a general conversation of several adults may seem like a cacophony due to super-sensitive detail-oriented hearing and perception tuned to literally pick up all elements of the conversation and the environment but downplay body language, sarcasm and non-literal cues. We can miss the forest for the trees when we start "overfitting," over-interpreting the noise on top of the actual signal. Ambient noise, trivial observations and unrelated perceptions may hide the true communication details.
During each communication (conversation) there are exchanges of both information and random noise. Fitting a perfect model is only listening to the “relevant” information. Over-fitting is when your attention is (excessively) consumed with the noise, or worse, letting the noise drown out the information exchange.
Any dataset is a mix of signal and noise. The main task of our brains are to sort these components and interpret the information (i.e., ignore the noise).
Our predictions are most accurate if we can model as much of the signal as possible and as little of the noise as possible. Note that in these terms, R2 is a poor metric to identify predictive power - it measures how much of the signal and the noise is explained by our model. In practice, it's hard to always identify what's signal and what's noise. This is why practical applications tends to favor simpler models, since the more complicated a model is the easier it is to overfit the noise component in the information.
Cross-validation is an iterative process, where each step involves:
- Randomly partitioning a sample of data into 2 complementary subsets (training + testing),
- Performing the analysis on the training subset
- Validating the analysis on the testing subset
- Increase the iteration index and repeat the process (termination criteria can involve a fixed number, or a desired (mean?) variability or error-rate).
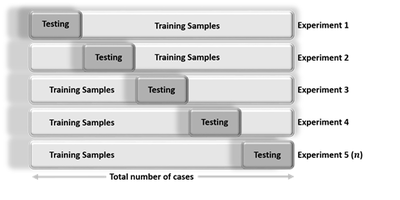
The validation results at each iteration are averaged, to reduce noise/variability, and reported.
Cross-validation guards against testing hypotheses suggested by the data themselves (aka: "Type III errors", False-Suggestion) in cases when new observations are hard to obtain (due to costs, reliability, time or other constraints).
Cross-validation is different from conventional-validation (e.g. 80%-20% partitioning the data set into training and testing subsets) as the in the conventional validation, the error (e.g. Root Mean Square Error, RMSE) on the training data is not a useful estimator of model performance, as it does not generalize across multiple samples. Errors of the conventional-valuation based on the results on the test data do not assess model performance, in general. A more fair way to properly estimate model prediction performance is to use cross-validation, which combines (averages) prediction errors or measures of fit to correct for the stochastic nature of training and testing data partitions and generate a more accurate and robust estimate of real model performance.
A more complex model overfits-the-data, relative to a simpler model when the former generates accurate fitting results for known data but less accurate results when predicting based on new data (foresight). Knowledge from past experience includes information either relevant or irrelevant (noise) for the future information. In challenging data-driven predict models when uncertainty (entropy) is high, more noise is present in past information that needs to be ignored in future forecasting. However it is generally hard to discriminate patterns from noise in complex systems (i.e., deciding which part to model and which to ignore). Models that reduce the chance of fitting noise are called robust.
Example (Linear Regression)
We can demonstrate model assessment using linear regression. Suppose we observe response values $\{y_1,...,y_n\}$, and the corresponding $k$ predictors represented as a $kD$ vector of covariates $\{x_1,...,x_n\}$, where subjects/cases are indexed by $1 ≤ i ≤ n$, and the data-elements (variables) are indexed by $1 ≤ j ≤ k$.
\begin{pmatrix} x_{1,1} & \cdots & x_{1,k} \\ \vdots & \ddots & \vdots \\ x_{n,1} & \cdots & x_{n,k} \end{pmatrix}
Using least squares to estimate the linear function parameters (effect-sizes), $\{β_1,...,β_k\}$, allows us to compute a hyperplane $y = a + xβ$ that best fits the observed data $\{x_i,y_i\}_{1≤i≤n}$.
\begin{equation} \begin{pmatrix} y_{1} \\ \vdots \\ y_{n} \end{pmatrix}
= \begin{pmatrix} α_{1} \\ \vdots \\ α_{n} \end{pmatrix}
+\begin{pmatrix} x_{1,1} & \cdots & x_{1,k} \\ \vdots & \ddots & \vdots \\ x_{n,1} & \cdots & x_{n,k} \end{pmatrix}
\begin{pmatrix} β_{1} \\ \vdots \\ β_{k} \end{pmatrix} \end{equation}
$$
\begin{array}{lcl}
y_1=\alpha_1+x_{1,1}\beta_1+x_{1,2}\beta_2+...+x_{1,k}\beta_k\\
y_2=\alpha_2+x_{2,1}\beta_1+x_{2,2}\beta_2+...+x_{2,k}\beta_k \\
...\\
y_n=\alpha_n+x_{n,1}\beta_1+x_{n,2}\beta_2+...+x_{n,k}\beta_k
\end{array}$$
The model fit may be evaluated using the mean squared error (MSE). The MSE for a given value of the parameters α and β on the observed training data $\{x_i,y_i\}_{1 ≤ i ≤ n}$.
$$ \begin{equation} MSE=\frac{1}{n}\sum_{i=1}^{n} \Bigg(y_i-\underbrace{(\alpha_1+x_{i,1}\beta_1+x_{i,2}\beta_2+\cdots+x_{i,k}\beta_k)}_{(\text{predicted value, } \hat{y_i} \text{, at }\{x_{i,1,}\cdots,x_{i,k}\})} \Bigg)^2 \end{equation} $$
$$ \begin{equation} RMSE=\sqrt{\frac{1}{n}\sum_{i=1}^{n} \Bigg(y_i-\underbrace{(\alpha_1+x_{i,1}\beta_1+x_{i,2}\beta_2+\cdots+x_{i,k}\beta_k)}_{(\text{predicted value, } \hat{y_i} \text{, at }\{x_{i,1,}\cdots,x_{i,k}\})} \Bigg)^2 }. \end{equation} $$
The expected value of the MSE (over the distribution of training sets) for the training set is $\frac{(n-k-1)}{(n + k + 1)} × E,$ where $E$ is the expected value of the MSE for the testing/validation data. Therefore, fitting a model and computing the MSE on the training set, we will get an over optimistic evaluation assessment (smaller RMSE) of how well the model may fit another dataset. This bias represents in-sample estimate of the fit, whereas we are interested in the cross-validation estimate as an out-of-sample estimate.
In the linear regression model, cross validation is not useful as we can compute the exact correction factor $\frac{(n - k - 1)}{(n + k + 1)}$ and correctly estimate the out-of-sample fit using the (MSE underestimate) in-sample MSE estimate. However, even in this situation, cross-validation remains useful as it can be used to select an optimal regularized cost function.
In most other modeling procedures (e.g. logistic regression), in general, there are no simple closed-form expressions (formulas) to adjust the cross-validation error estimate from the in-sample fit estimate. Cross-validation is generally applicable way to predict the performance of a model on a validation set using stochastic computation instead of obtaining experimental, theoretical, mathematical, or analytic error estimates.
Cross-validation methods
There are 2 classes of cross-validation approaches – exhaustive and non-exhaustive.
Exhaustive cross-validation
Exhaustive cross-validation methods are based on determining all possible ways to divide the original sample into training and testing data. For example, the Leave-m-out cross-validation involves using $m$ observations for testing and the remaining ($n-m$) observations as training (when $m=1$, leave-1-out method). This process is repeated on all partitions of the original sample. This method requires model fitting and validating $C_m^n$ times ($n$ is the total number of observations in the original sample and $m$ is the number left out for validation). This requires a very large number of steps1.
Non-exhaustive cross-validation
Non-exhaustive cross validation methods avoid computing estimates/errors using all possible partitionings of the original sample, but rather approximates these. For example, in the k-fold cross-validation, the original sample is randomly partitioned into $k$ equal sized subsamples. Of the $k$ subsamples, a single subsample is kept as final testing data for validation of the model. The other $k- 1$ subsamples are used as training data. The cross-validation process is then repeated $k$ times ($k$ folds). Each of the $k$ subsamples is used once as the validation data. There are corresponding $k$ results that are averaged (or otherwise aggregated) to generate a final model-quality estimation. In $k$-fold validation, all observations are used for both training and validation, and each observation is used for validation exactly once. In general, $k$ is a parameter that needs to be selected by investigator (common values may be 5, 10).
A general case of the $k$-fold validation is $k=n$ (the total number of observations), when it coincides with the leave-one-out cross-validation.
A variation of the $k$-fold validation is stratified k-fold cross-validation, where each fold has the same (approximately) mean response value. For instance, if the model represents a binary classification of cases (e.g., NC vs. PD), this implies that each fold contains roughly the same proportion of the 2 class labels.
Repeated random sub-sampling validation splits randomly the entire dataset into training (where the model is fit) and testing data where the predictive accuracy is assessed). Again, the results are averaged over all iterative splits. This method has an advantage over $k$-fold cross validation as that the proportion of the training/testing split is not dependent on the number of iterations (folds). However, its drawback is that some observations may never be selected whereas others may be selected multiple-times in the testing/validation subsample, as validation subsets may overlap, and the results will vary each time we repeat the validation protocol (unless we set a seed point in the algorithm).
Asymptotically, as the number of random splits increases, the repeated random sub-sampling validation approaches the leave-k-out cross-validation.
Case-Studies
Example 1: Parkinson’s Diseases Study involving neuroimaging, genetics, clinical, and phenotypic data for over 600 volunteers produced multivariate data for 3 cohorts (HC=Healthy Controls, PD=Parkinson’s, SWEDD= subjects without evidence for dopaminergic deficit).
# update packages
# update.packages()
#load the data: 06_PPMI_ClassificationValidationData_Short.csv
ppmi_data <-read.csv("https://umich.instructure.com/files/330400/download?download_frd=1",header=TRUE)
#binarize the Dx classes
ppmi_data$\$$ResearchGroup <- ifelse(ppmi_data$\$$ResearchGroup == "Control", "Control", "Patient")
attach(ppmi_data)
head(ppmi_data)
# Model-free analysis, classification
# install.packages("crossval")
#library("crossval")
require(crossval)
require(ada)
#set up adaboosting prediction function
#Define a new classification result-reporting function
my.ada <- function (train.x, train.y, test.x, test.y, negative, formula){
ada.fit <- ada(train.x, train.y)
predict.y <- predict(ada.fit, test.x)
#count TP, FP, TN, FN, Accuracy, etc.
out <- confusionMatrix(test.y, predict.y, negative = negative)
#negative is the label of a negative "null" sample (default: "control").
return (out)
}
#balance cases
#SMOTE: Synthetic Minority Oversampling Technique to handle class misbalance in binary classification.
set.seed(1000)
#install.packages("unbalanced") to deal with unbalanced group data
require(unbalanced)
ppmi_data$\$$PD <- ifelse(ppmi_data$\$$ResearchGroup=="Control",1,0)
uniqueID <- unique(ppmi_data$\$$FID_IID)
ppmi_data <- ppmi_data[ppmi_data$\$$VisitID==1,]
ppmi_data$\$$PD <- factor(ppmi_data$\$$PD)
colnames(ppmi_data)
#ppmi_data.1<-ppmi_data[,c(3:281,284,287,336:340,341)]
n <- ncol(ppmi_data)
output.1 <- ppmi_data$\$$PD
# remove Default Real Clinical subject classifications!
ppmi_data$\$$PD <- ifelse(ppmi_data$\$$ResearchGroup=="Control",1,0)
input <- ppmi_data[ ,-which(names(ppmi_data) %in% c("ResearchGroup","PD", "X", "FID_IID"))]
# output <- as.matrix(ppmi_data[ ,which(names(ppmi_data) %in% {"PD"})])
output <- as.factor(ppmi_data$\$$PD)
c(dim(input), dim(output))
# balance the dataset
data.1<-ubBalance(X= input, Y=output, type="ubSMOTE", percOver=300, percUnder=150, verbose=TRUE)
balancedData<-cbind(data.1$\$$X, data.1$\$$Y)
nrow(data.1$\$$X); ncol(data.1$\$$X)
nrow(balancedData); ncol(balancedData)
nrow(input); ncol(input)
colnames(balancedData) <- c(colnames(input), "PD")
###Check balance
##T test
alpha.0.05 <- 0.05
test.results.bin <- NULL # binarized/dichotomized p-values
test.results.raw <- NULL # raw p-values
# get a better error-handling t.test function that gracefully handles NA’s and trivial variances
my.t.test.p.value <- function(input1, input2) {
obj <- try(t.test(input1, input2), silent=TRUE)
if (is(obj, "try-error")) return(NA) else return(obj$\$$p.value''')
}
for (i in 1:ncol(balancedData))
{
test.results.raw[i] <- my.t.test.p.value(input[,i], balancedData [,i])
test.results.bin[i] <- ifelse(test.results.raw[i] > alpha.0.05, 1, 0)
# binarize the p-value (0=significant, 1=otherwise)
print(c("i=", i, "var=", colnames(balancedData[i]), "t-test_raw_p_value=", test.results.raw[i]))
}
#we can also employ (e.g., FDR, Bonferonni) <u>'''correction for multiple testing'''</u>!
#test.results.corr <- '''stats::p.adjust'''(test.results.raw, method = "fdr", n = length(test.results.raw))
#where methods are "holm", "hochberg", "hommel", "bonferroni", "BH", "BY", "fdr", "none")
#plot(test.results.raw, test.results.corr)
#sum(test.results.raw < alpha.0.05, na.rm=T)/length(test.results.raw) #check proportion of inconsistencies
#sum(test.results.corr < alpha.0.05, na.rm =T)/length(test.results.corr)
#as the sample-size is changed:
length(input[,5]); length(balancedData [,5])
#to plot raw vs. rebalanced pairs (e.g., var="L_insular_cortex_Volume"), we need to equalize the lengths
plot (input[,5] +0*balancedData [,5], balancedData [,5]) # [,5] == "L_insular_cortex_Volume"
print(c("T-test results: ", test.results))
#zeros (0) are significant independent between-group T-test differences, ones (1) are insignificant
for (i in 1:(ncol(balancedData)-1))
{
test.results.raw [i] <- wilcox.test(input[,i], balancedData [,i])$\$$p.value
test.results.bin [i] <- ifelse(test.results.raw [i] > alpha.0.05, 1, 0)
print(c("i=", i, "Wilcoxon-test=", test.results.raw [i]))
}
print(c("Wilcoxon test results: ", test.results.bin))
#test.results.corr <- stats::p.adjust(test.results.raw, method = "fdr", n = length(test.results.raw))
#where methods are "holm", "hochberg", "hommel", "bonferroni", "BH", "BY", "fdr", "none")
#plot(test.results.raw, test.results.corr)
#cross validation
#using raw data: X <- as.data.frame(input); Y <- output neg <- "1" # "Control" == "1"
#using Rebalanced data:
X <- as.data.frame(data.1$\$$X); Y <- data.1$\$$Y #balancedData<-cbind(data.1$\$$X, data.1$\$$Y); dim(balancedData)
#Side note: There is a function name collision for “crossval”, the same method is present in
#the “mlr” (machine Learning in R) package and in the “crossval” package.
#To specify a function call from a specific package do: packagename::functionname()
set.seed(115)
#cv.out <- crossval::crossval(my.ada, X, Y, K = 5, B = 1, negative = neg)
cv.out <- crossval::crossval(my.ada, X, Y, K = 5, B = 1, negative = neg)
#the label of a negative "null" sample (default: "control")
out <- diagnosticErrors(cv.out$\$$stat)
print(cv.out$\$$stat)
print(out)
| FP | TP | TN | FN |
| 1.0 | 59.8 | 23.4 | 0.2 |
| acc | sens | spec | ppv | npv | lor |
| 0.9857820 | 0.9966667 | 0.9590164 | 0.9835526 | 0.9915254 | 8.8531796 |
#Define a new LDA = Linear discriminant analysis predicting function
require("MASS") # for lda function
predfun.lda = function(train.x, train.y, test.x, test.y, negative)
{ lda.fit = lda(train.x, grouping=train.y)
ynew = predict(lda.fit, test.x)$\$$class
#count TP, FP etc.
out = confusionMatrix(test.y, ynew, negative=negative)
return( out )
}
'''(1) a simple example using the sleep dataset''' (containing the effect of two soporific drugs to increase hours of sleep (treatment-compared design) on 10 patients)
data(sleep)
X = as.matrix(sleep[,1, drop=FALSE]) # increase in hours of sleep,
# drop is logical, if TRUE the result is coerced to the lowest possible dimension.
#The default is to drop if only one column is left, but not to drop if only one row is left.
Y = sleep[,2] # drug given
plot(X ~ Y)
levels(Y) # "1" "2"
dim(X) # 20 1
set.seed(123456)
cv.out <- '''crossval::crossval'''(predfun.lda, X, Y, K=5, B=20, negative="1")
cv.out$\$$stat
diagnosticErrors(cv.out$\$$stat)
'''(2) A model-based example (linear regression) using the attitude dataset:'''
'''#?attitude, colnames(attitude)'''
#"rating" "complaints" "privileges" "learning" "raises" "critical" "advance"
#aggregated survey of clerical employees of an organization, representing 35 employees of 30
#(randomly selected) departments. Data=percent proportion of favorable responses to 7 questions in each department.
#Note: when using a data frame, a time-saver is to use “.” to indicate “include all covariates" in the DF.
#E.g., fit <- lm(Y ~ ., data = D)
data("attitude")
y = attitude[,1] # rating variable
x = attitude[,-1] # date frame with the remaining variables
is.factor(y)
summary( lm(y ~ . , data=x) ) # R-squared: 0.7326
#set up lm prediction function
'''predfun.lm = function(train.x, train.y, test.x, test.y)'''
{ lm.fit = lm(train.y ~ . , data=train.x)
ynew = predict(lm.fit, test.x )
#compute squared error risk (MSE)
out = mean( (ynew - test.y)^2)
<span style="background-color: #32cd32">#note that, in general, when fitting linear model to continuous outcome variable (Y),</span>
<span style="background-color: #32cd32">#we can’t use the '''out<-confusionMatrix(test.y, ynew, negative=negative)''', as it requires a binary outcome</span>
<span style="background-color: #32cd32">#this is why we use the MSE as an estimate of the discrepancy between observed & predicted values</span>
return(out)
}
#require("MASS")
'''predfun.lda = function(train.x, train.y, test.x, test.y, negative)'''
{ lda.fit = lda(train.x, grouping=train.y)
ynew = predict(lda.fit, test.x)$\$$class
#count TP, FP etc.
out = confusionMatrix(test.y, ynew, negative=negative)
return( out )
}
#prediction MSE using all variables
set.seed(123456)
cv.out.lm = crossval::crossval(predfun.lm, x, y, K=5, B=20, negative="1")
c(cv.out.lm$\$$stat, cv.out.lm$\$$stat.se) # 72.581198 3.736784
#reducing to using only two variables
cv.out.lm = crossval::crossval(predfun.lm, x[,c(1,3)], y, K=5, B=20, negative="1")
c(cv.out.lm$\$$stat, cv.out.lm$\$$stat.se) # 52.563957 2.015109
(3) a real example using the ppmi_data
#ppmi_data <-read.csv("https://umich.instructure.com/files/330400/download?download_frd=1",header=TRUE)
#ppmi_data$\$$ResearchGroup <- ifelse(ppmi_data$\$$ResearchGroup == "Control", "Control", "Patient")
#attach(ppmi_data); head(ppmi_data)
#install.packages("crossval")
#library("crossval")
#ppmi_data$\$$PD <- ifelse(ppmi_data$\$$ResearchGroup=="Control",1,0)
#input <- ppmi_data[ ,-which(names(ppmi_data) %in% c("ResearchGroup","PD", "X", "FID_IID"))]
#output <- as.factor(ppmi_data$\$$PD)
#remove the irrelevant variables (e.g., visit ID)
output <- as.factor(ppmi_data$\$$PD)
input <- ppmi_data[, -which(names(ppmi_data) %in% c("ResearchGroup","PD", "X", "FID_IID", "VisitID"))]
X = as.matrix(input) # Predictor variables
Y = as.matrix(output) # Actual PD clinical assessment
dim(X); dim(Y)
layout(matrix(c(1,2,3,4),2,2)) # optional 4 graphs/page
fit <- lm(Y~X); plot(fit) # plot the fit
levels(as.factor(Y)) # "0" "1"
c(dim(X), dim(Y)) # 1043 103
set.seed(12345)
#cv.out.lm = crossval::crossval(predfun.lm, as.data.frame(X), as.numeric(Y), K=5, B=20)
cv.out.lda = crossval::crossval(predfun.lda, X, Y, K=5, B=20, negative="1")
#K=Number of folds; B=Number of repetitions.
#Results
cv.out.lda$\$$stat; cv.out.lda; diagnosticErrors(cv.out.lda$\$$stat)
cv.out.lm$\$$stat; cv.out.lm; diagnosticErrors(cv.out.lm$\$$stat)
The cross-validation (CV) output object includes the following components:
- stat.cv: Vector od statistics returned by predfun for each cross validation run
- stat: Mean the statistic returned by predfun averaged over all cross validation runs
- stat.se: Variability: the corresponding standard error.
| FP | TP | TN | FN |
| 0.06 | 96.94 | 33.14 | 2.06 |
| acc | sens | spec | ppv | npv | lor |
| 0.9839637 | 0.9791919 | 0.9981928 | 0.9993814 | 0.9414773 | 10.1655380 |
Alternative predictor functions
Logistic Regression
(See the earlier batch of class notes, https://umich.instructure.com/files/421847/download?download_frd=1)
#ppmi_data <-
read.csv("https://umich.instructure.com/files/330400/download?download_frd=1",header=TRUE)
# ppmi_data$\$$ResearchGroup <- ifelse(ppmi_data$\$$ResearchGroup == "Control", "Control", "Patient")
#install.packages("crossval"); library("crossval")
#ppmi_data$\$$PD <- ifelse(ppmi_data$\$$ResearchGroup=="Control",1,0)
#remove the irrelevant variables (e.g., visit ID)
output <- as.factor(ppmi_data$\$$PD)
input <- ppmi_data[, -which(names(ppmi_data) %in% c("ResearchGroup","PD", "X", "FID_IID", "VisitID"))]
X = as.matrix(input) # Predictor variables
Y = as.matrix(output)
<span style="background-color: #32cd32">'''Note that the predicted values are in LOG terms, so we need to exponentiate them to interpret them correctly'''</span>
lm.logit <- glm(as.numeric(Y) ~ ., data = as.data.frame(X), family = "binomial")
ynew <- predict(lm.logit, as.data.frame(X)); plot(ynew)
ynew2 <- ifelse(exp(ynew)<0.5, 0, 1); plot(ynew2)
'''predfun.logit = function(train.x, train.y, test.x, test.y, neg)'''
{ lm.logit <- glm(train.y ~ ., data = train.x, family = "binomial")
ynew = predict(lm.logit, test.x )
#compute TP, FP, TN, FN
<span style="background-color: #32cd32">ynew2</span> <- ifelse(exp(ynew)<0.5, 0, 1)
out = confusionMatrix(test.y, ynew2, negative=neg) # Binary outcome, we can use confusionMatrix
return( out )
}
#Reduce the bag of explanatory variables, purely to simplify the interpretation of the analytics in this example!
input.short <- input[, which(names(input) %in% c("R_fusiform_gyrus_Volume",
"R_fusiform_gyrus_ShapeIndex", "R_fusiform_gyrus_Curvedness",
"Sex", "Weight", "Age" , "chr12_rs34637584_GT", "chr17_rs11868035_GT",
"UPDRS_Part_I_Summary_Score_Baseline", "UPDRS_Part_I_Summary_Score_Month_03",
"UPDRS_Part_II_Patient_Questionnaire_Summary_Score_Baseline",
"UPDRS_Part_III_Summary_Score_Baseline",
"X_Assessment_Non.Motor_Epworth_Sleepiness_Scale_Summary_Score_Baseline"
))]
X = as.matrix(input.short)
cv.out.logit = '''crossval::crossval'''(predfun.logit, as.data.frame(X), as.numeric(Y), K=5, B=2, neg="1")
cv.out.logit$\$$stat.cv
diagnosticErrors(cv.out.logit$\$$stat)
<span style="background-color: #32cd32">Caution:</span> Note that if you forget to exponentiate the predicted logistic model values (see ynew2 in predict.logit), you will get nonsense results (e.g., all cases are predicted to be in one class, trivial sensitivity or NPP).
predfun.qda = function(train.x, train.y, test.x, test.y, negative)
{
require("MASS") # for lda function
qda.fit = qda(train.x, grouping=train.y)
ynew = predict(qda.fit,test.x)$\$$class
out.qda = confusionMatrix(test.y, ynew, negative=negative)
return( out.qda )
}
cv.out.qda = crossval::crossval(predfun.qda, as.data.frame(input.short), as.factor(Y), K=5, B=20, neg="1")
diagnosticErrors(cv.out.lda$\$$stat); diagnosticErrors(cv.out.qda$\$$stat);
This error message: “Error in qda.default(x, grouping, ...) : rank deficiency in group 1” indicates that there is a rank deficiency, i.e. some variables are collinear and one or more covariance matrices cannot be inverted to obtain the estimates in group 1 (Controls)!
If you remove the strongly correlated data elements ("R_fusiform_gyrus_Volume","R_fusiform_gyrus_ShapeIndex", and "R_fusiform_gyrus_Curvedness"), the rank-deficiency problem goes away!
input.short2 <- input[, which(names(input) %in%)"R_fusiform_gyrus_Volume",
"Sex", "Weight", "Age" , "chr17_rs11868035_GT",
"UPDRS_Part_I_Summary_Score_Baseline",
"UPDRS_Part_II_Patient_Questionnaire_Summary_Score_Baseline",
"UPDRS_Part_III_Summary_Score_Baseline",
"X_Assessment_Non.Motor_Epworth_Sleepiness_Scale_Summary_Score_Baseline"
))]
X = as.matrix(input.short2)
cv.out.qda = crossval::crossval(predfun.qda, as.data.frame(X), as.numeric(Y), K=5, B=2, neg="1")
Compare the QDA and GLM/Logit predictions:
diagnosticErrors(cv.out.qda$\$$stat); diagnosticErrors(cv.out.logit$\$$stat)
1http://www.ohrt.com/odds/binomial.php
See also
- Next Section: Foundation of LDA and QDA for prediction, dimensionality reduction or forecasting
- Structural Equation Modeling (SEM)
- Growth Curve Modeling (GCM)
- Generalized Estimating Equation (GEE) Modeling
- Back to Big Data Science
- SOCR Home page: http://www.socr.umich.edu
Translate this page: