Difference between revisions of "SOCR EduMaterials Activities Normal Distributions"
(→This is an activity to explore some continuous distributions and the normal approximation to binomial and Poisson.) |
(→This is an activity to explore some continuous distributions and the normal approximation to binomial and Poisson.) |
||
| Line 11: | Line 11: | ||
x_p=\frac{ln(1-\frac{p}{100})}{-\lambda} | x_p=\frac{ln(1-\frac{p}{100})}{-\lambda} | ||
</math> | </math> | ||
| − | + | *'''4.''' Compute one cumulative probability for each one of these distributions, show it on the graph, and verify it with the formula: | |
<math> | <math> | ||
P(X \le x)=1-e^{-\lambda x} | P(X \le x)=1-e^{-\lambda x} | ||
Revision as of 23:20, 24 November 2006
This is an activity to explore some continuous distributions and the normal approximation to binomial and Poisson.
- Description: You can access the applets for the above distributions at http://www.socr.ucla.edu/htmls/SOCR_Distributions.html .
- Exercise 1: \item[a.] Graph and print \( X \sim exp(0.2) \), \( X \sim exp(1) \), \( X \sim exp(10) \)
- 1. Locate the maximum density for each one of these distributions.
- 2. Find the height of the density at 3 values of \( X \) (one near 0, one near the mean, and one towards the tail of the distribution).
- 3. Find one percentile for each of these distributions and record them on the printouts. Verify these percentiles using the formula we discussed in class\[ x_p=\frac{ln(1-\frac{p}{100})}{-\lambda} \]
- 4. Compute one cumulative probability for each one of these distributions, show it on the graph, and verify it with the formula\[ P(X \le x)=1-e^{-\lambda x} \]
- Exercise 2: Use SOCR to graph and print the distribution of \( X \sim N(20, 3) \). Show on the graph the following points\[\mu \pm 1 \sigma, \mu \pm 2 \sigma, \mu \pm 3 \sigma \]. How many standard deviations from the mean is the value \( x=27.5 \)?
- Exercise 3: Graph the distribution of \( X \sim N(40, 10) \).
- 1. Find \( P(X>49)\) Submit a printout.
- 2. Find \(P(X<22)\) Submit a printout.
- 3. Find \(P(X<58)\) Submit a printout.
- 4. Find \(P(X>13)\) Submit a printout.
- 5. Find \(P(12<X<37)\) Submit a printout.
- 6. Find \( P(33<X<60)\) Submit a printout.
- 7. Find \( P(52<X<65)\) Submit a printout.
- 8. Use the mouse or the left cut off or right cut off points to find the \(8_{th}, 20_{th}, 45_{th}, 55_{th}$, $70_{th}, 95_{th}\) percentiles. After you find these percentiles you can place by hand all of them in one printout (or you can submit a printout for each one of them if you want).
- 9. Make sure you know how to answer the above questions using the \(z\) score \(z=\frac{x-\mu}{\sigma}\) and your \(z\) table from the handout! You do not need to submit anything here.
- Exercise 3: The lifetime of tires of brand A follows the normal distribution with mean 40000 miles and standard deviation 4000 miles.
- 1. Use SOCR to find the probability that a tire will last between 40000 and 46000 miles.
- 2. Given that a tire will last more than 46000 miles what is the probability that it will last more than 50000 miles? Submit a printout and explain how you get the answer.
- 3. Given that a tire will last more than 46000 miles what is the probability that it will last less than 50000 miles? Submit a printout and explain how you get the answer.
- Exercise 4: The probability that a student is admitted in the Math Department Major at a college is <math.30 \%</math>. Suppose that this year 150 students will apply for admission into the Math major.
- 1. What is the distribution of the number of students admitted? Use $SOCR$ to graph and print this distribution. What is the shape of this distribution? What is the mean and standard deviation of this distribution?
- 2. Write an expression for the exact probability that among the 150 students at least 55 will be admitted.
- 3. Use SOCR to compute the probability of part (2).
- 4. Use the normal distribution to approximate the probability of part (2) (do not forget the continuity correction). What is the error of the approximation?
- Exercise 5: The number of pine trees per acre in a forest follows the Poisson distribution with mean 30.
- 1. Graph and print this distribution.
- 2. What is the shape of this distribution? Why?
- 3. Use SOCR to find the probability that an acre has more than 37 pines.
- 4. Approximate the probability of part (c) using the normal distribution.
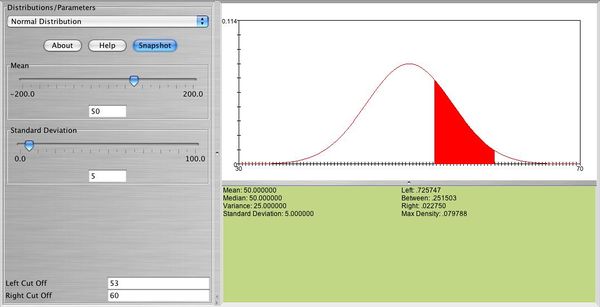
Below you can see the distribution of a normal random variable \( X \) with \( \mu=50, \ \sigma=5 \). In this graph you can also see the probability that \( X \) is between 53 and 60.
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
</math>