Difference between revisions of "SOCR EduMaterials Activities Poisson Distribution"
m (Reverted edit of EvkWtl, changed back to last version by IvoDinov) |
|||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 20: | Line 20: | ||
* '''Exercise 5:''' People enter a gambling casino at a rate of 1 for every two minutes. | * '''Exercise 5:''' People enter a gambling casino at a rate of 1 for every two minutes. | ||
** What is the probability that no one enters between 12:00 and 12:05? | ** What is the probability that no one enters between 12:00 and 12:05? | ||
| − | * What is the probability that at least 4 people enter the casino during that time? | + | ** What is the probability that at least 4 people enter the casino during that time? |
* '''Exercise 6:''' Let <math>X_1</math> denote the number of vehicles passing a particular point on the eastbound lane of a highway in 1 hour. Suppose that the Poisson distribution with mean <math>\lambda_1=5</math> is a reasonable model for <math>X_1</math>. Now, let <math>X_2</math> denote the number of vehicles passing a point on the westbound lane of the same highway in 1 hour. Suppose that <math>X_2</math> has a Poisson distribution with mean <math>\lambda_2= 3</math>. Of interest is <math>Y= X_1 + X_2</math>, the total traffic count in both lanes in one hour. What is the <math>P(Y < 5) ?</math> | * '''Exercise 6:''' Let <math>X_1</math> denote the number of vehicles passing a particular point on the eastbound lane of a highway in 1 hour. Suppose that the Poisson distribution with mean <math>\lambda_1=5</math> is a reasonable model for <math>X_1</math>. Now, let <math>X_2</math> denote the number of vehicles passing a point on the westbound lane of the same highway in 1 hour. Suppose that <math>X_2</math> has a Poisson distribution with mean <math>\lambda_2= 3</math>. Of interest is <math>Y= X_1 + X_2</math>, the total traffic count in both lanes in one hour. What is the <math>P(Y < 5) ?</math> | ||
Latest revision as of 18:47, 17 August 2007
This is an activity to explore the Poisson Probability Distribution.
- Description: You can access the applets for the above distributions at http://www.socr.ucla.edu/htmls/SOCR_Distributions.html .
- Exercise 1: Use SOCR to graph and print the distribution of a Poisson random variable with \( \lambda=2 \). What is the shape of this distribution?
- Exercise 2: Use SOCR to graph and print the distribution of a Poisson random variable with \( \lambda=15 \). What is the shape of this distribution? What happens when you keep increasing \( \lambda \)?
- Exercise 3: Let \( X \sim Poisson(5) \). Find \( P(3 \le X < 10) \), and \( P(X >10 | X \ge 4) \).
- Exercise 4: Poisson approximation to binomial: Graph and print \( X \sim b(60, 0.02) \). Approximate this probability distribution using Poisson. Choose three values of \( X \) and compute the probability for each one using Poisson and then using binomial. How good is the approximation?
Below you can see the distribution of a Poisson random variable with \( \lambda=5 \). In this graph you can also see the probability that between 2 and 5 events will occur.
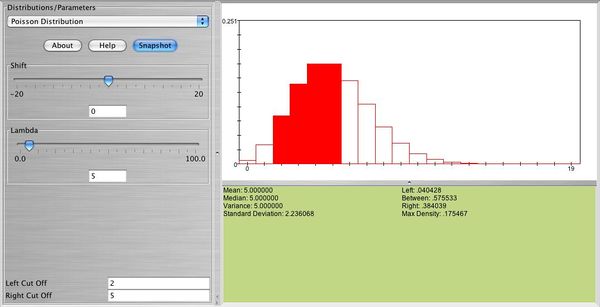
- Exercise 5: People enter a gambling casino at a rate of 1 for every two minutes.
- What is the probability that no one enters between 12:00 and 12:05?
- What is the probability that at least 4 people enter the casino during that time?
- Exercise 6: Let \(X_1\) denote the number of vehicles passing a particular point on the eastbound lane of a highway in 1 hour. Suppose that the Poisson distribution with mean \(\lambda_1=5\) is a reasonable model for \(X_1\). Now, let \(X_2\) denote the number of vehicles passing a point on the westbound lane of the same highway in 1 hour. Suppose that \(X_2\) has a Poisson distribution with mean \(\lambda_2= 3\). Of interest is \(Y= X_1 + X_2\), the total traffic count in both lanes in one hour. What is the \(P(Y < 5) ?\)
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
</math>