AP Statistics Curriculum 2007 Prob Rules

General Advance-Placement (AP) Statistics Curriculum - Probability Theory Rules

Addition Rule

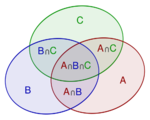
The probability of a union, also called the Inclusion-Exclusion principle allows us to compute probabilities of composite events represented as unions (i.e., sums) of simpler events.

Venn Diagrams

For events A₁, ..., A_n in a probability space (S,P), the probability of the union for n=2 is \[P(A_1\cup A_2)=P(A_1)+P(A_2)-P(A_1\cap A_2),\]

For n=3, \[P(A_1\cup A_2\cup A_3)=P(A_1)+P(A_2)+P(A_3) -P(A_1\cap A_2)-P(A_1\cap A_3)-P(A_2\cap A_3)+P(A_1\cap A_2\cap A_3)\]

In general, for any n, \[P(\bigcup_{i=1}^n A_i) =\sum_{i=1}^n P(A_i) -\sum_{i,j\,:\,i<j}P(A_i\cap A_j) +\sum_{i,j,k\,:\,i<j<k}P(A_i\cap A_j\cap A_k)+ \cdots\cdots\ +(-1)^{j+1} P(\bigcap_{i=1}^j A_i)+ \cdots\cdots\ +(-1)^{n+1} P(\bigcap_{i=1}^n A_i).\]

Conditional Probability

The conditional probability of A occurring given that B occurs is given by \[P(A | B) ={P(A \cap B) \over P(B)}.\]

Example

Here is the data on 400 Melanoma (skin cancer) Patients by Type and Site

	Site
Type	Head and Neck	Trunk	Extremities	Totals
Hutchinson's melanomic freckle	22	2	10	34
Superficial	16	54	115	185
Nodular	19	33	73	125
Indeterminant	11	17	28	56
Column Totals	68	106	226	400

• Suppose we select one out of the 400 patients in the study and we want to find the probability that the cancer is on the extremities given that it is of type nodular: P = 73/125 = P(Extremities | Nodular)

• What is the probability that for a randomly chosen patient the cancer type is Superficial given that it appears on the Trunk?

Example - Monty Hall Problem

Recall that earlier we discussed the Monty Hall Experiment. We will now show why the odds of winning double if we use the swap strategy - that is the probability of a win is 2/3, if each time we switch and choose the last third card.

Denote W={Final Win of the Car Price}. Let L₁ and W₂ represent the events of choosing the donkey (loosing) and the car (winning) at the player's first and second choice, respectively. Then, the chance of winning in the swapping-strategy case is\[P(W) = P(L_1 \cap W_2) = P(W_2 | L_1) P(L_1) = 1 \times {2\over 3} ={2\over 3}\]. If we played using the stay-home strategy, our chance of winning would have been\[P(W) = P(W_1 \cap W_2) = P(W_2 | W_1) P(W_1) = 1 \times {1\over 3} ={1\over 3}\], or half the chance in the first (swapping) case.

Model Validation

Checking/affirming underlying assumptions.

• TBD

Computational Resources: Internet-based SOCR Tools

• TBD

Examples

Computer simulations and real observed data.

• TBD

Hands-on activities

Step-by-step practice problems.

• TBD

---

References

• TBD

---

• SOCR Home page: http://www.socr.ucla.edu

---

---

Translate this page:

(default)	Deutsch	Español	Français	Italiano	Português	日本語	България	الامارات العربية المتحدة	Suomi	इस भाषा में	Norge
한국어	中文	繁体中文	Русский	Nederlands	Ελληνικά	Hrvatska	Česká republika	Danmark	Polska	România	Sverige