Difference between revisions of "AP Statistics Curriculum 2007 Beta"
(→Example) |
|||
| (7 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| + | ==[[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - Beta Distribution== | ||
| + | |||
===Beta Distribution=== | ===Beta Distribution=== | ||
'''Definition''': Beta distribution is a distribution that models events which are constrained to take place within an interval defined by a minimum and maximum value. | '''Definition''': Beta distribution is a distribution that models events which are constrained to take place within an interval defined by a minimum and maximum value. | ||
| − | <br />'''Probability density function''': For <math>X\sim Beta(\alpha,\beta)\!</math>, the Beta probability density function is given by | + | <br />'''Probability density function''': For <math>X\sim \operatorname{Beta}(\alpha,\beta)\!</math>, the Beta probability density function is given by |
:<math>\frac{x^{\alpha-1}(1-x)^{\beta-1}}{\Beta(\alpha,\beta)}</math> | :<math>\frac{x^{\alpha-1}(1-x)^{\beta-1}}{\Beta(\alpha,\beta)}</math> | ||
| Line 9: | Line 11: | ||
*<font size="3"><math>\alpha</math></font> is a positive shape parameter | *<font size="3"><math>\alpha</math></font> is a positive shape parameter | ||
*<font size="3"><math>\beta</math></font> is a positive shape parameter | *<font size="3"><math>\beta</math></font> is a positive shape parameter | ||
| − | *<math>\textstyle\Beta(\alpha,\beta)=\int_0^1 t^{\alpha-1}(1-t)^{\beta-1}dt</math> or | + | *<math>\textstyle\Beta(\alpha,\beta)=\int_0^1 t^{\alpha-1}(1-t)^{\beta-1}dt</math> or <br /><math>\textstyle\Beta(\alpha,\beta)=\frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}</math>, where <math>\Gamma(k)!=(k-1)!=1 \times 2 \times\ 3 \times\cdots \times (k-1)</math> |
| − | |||
*x is a random variable | *x is a random variable | ||
| Line 37: | Line 38: | ||
*The time it takes to complete a task | *The time it takes to complete a task | ||
*The proportion of defective items in a shipment | *The proportion of defective items in a shipment | ||
| − | |||
===Example=== | ===Example=== | ||
| Line 48: | Line 48: | ||
The figure below shows this result using [http://socr.ucla.edu/htmls/dist/Beta_Distribution.html SOCR distributions] | The figure below shows this result using [http://socr.ucla.edu/htmls/dist/Beta_Distribution.html SOCR distributions] | ||
<center>[[Image:Beta.jpg|600px]]</center> | <center>[[Image:Beta.jpg|600px]]</center> | ||
| + | |||
| + | <hr> | ||
| + | * SOCR Home page: http://www.socr.ucla.edu | ||
| + | |||
| + | "{{translate|pageName=http://wiki.socr.umich.edu/index.php/AP_Statistics_Curriculum_2007_Beta}} | ||
Latest revision as of 05:51, 4 April 2023
Contents
General Advance-Placement (AP) Statistics Curriculum - Beta Distribution
Beta Distribution
Definition: Beta distribution is a distribution that models events which are constrained to take place within an interval defined by a minimum and maximum value.
Probability density function: For \(X\sim \operatorname{Beta}(\alpha,\beta)\!\), the Beta probability density function is given by
\[\frac{x^{\alpha-1}(1-x)^{\beta-1}}{\Beta(\alpha,\beta)}\]
where
- \(\alpha\) is a positive shape parameter
- \(\beta\) is a positive shape parameter
- \(\textstyle\Beta(\alpha,\beta)=\int_0^1 t^{\alpha-1}(1-t)^{\beta-1}dt\) or
\(\textstyle\Beta(\alpha,\beta)=\frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}\), where \(\Gamma(k)!=(k-1)!=1 \times 2 \times\ 3 \times\cdots \times (k-1)\) - x is a random variable
Cumulative density function: Beta cumulative distribution function is given by
\[\frac{\Beta_x(\alpha,\beta)}{\Beta(\alpha,\beta)}\]
where
- \(\textstyle\Beta_x(\alpha,\beta)=\int_0^x t^{\alpha-1}(1-t)^{\beta-1}dt\)
- \(\textstyle\Beta(\alpha,\beta)=\int_0^1 t^{\alpha-1}(1-t)^{\beta-1}dt\)
Moment generating function: The Beta moment-generating function is
\[M(t)=1+\sum_{k=1}^\infty (\prod_{r=0}^{k-1}\frac{\alpha+r}{\alpha+\beta+r})\frac{t^k}{k!}\]
Expectation: The expected value of a Beta distributed random variable x is
\[E(X)=\frac{\alpha}{\alpha+\beta}\]
Variance: The Beta variance is
\[Var(X)=\frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}\]
Applications
The Beta distribution is used in a range of disciplines including rule of succession, Bayesian statistics, and task duration modeling. Examples of events that may be modeled by Beta distribution include:
- The time it takes to complete a task
- The proportion of defective items in a shipment
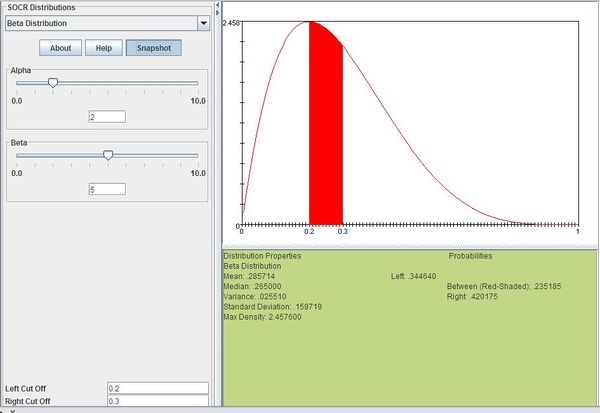
Example
Suppose that DVDs in a certain shipment are defective with a Beta distribution with \(\alpha=2\) and \(\beta=5\). Compute the probability that the shipment has 20% to 30% defective DVDs.
We can compute this as follows:
\[P(0.2\le X\le 0.3)=\sum_{x=0.2}^{0.3}\frac{x^{2-1}(1-x)^{5-1}}{\Beta(2,5)}=0.235185\]
The figure below shows this result using SOCR distributions
- SOCR Home page: http://www.socr.ucla.edu
"-----
Translate this page: