Difference between revisions of "SMHS ROC"
(→Theory) |
(→R AUC/ROC Example) |
||
| (45 intermediate revisions by the same user not shown) | |||
| Line 6: | Line 6: | ||
===Motivation=== | ===Motivation=== | ||
| − | We have talked about the cases with a binary classification where the outcomes are either absent or present and the test results are positive or negative. We have also discussed | + | We have talked about the cases with a binary classification where the outcomes are either absent or present and the test results are positive or negative. We have also previously discussed [[SMHS_PowerSensitivitySpecificity|sensitivity and specificity]] which are associated with the concepts of true positive and true negatives. With ROC curve, we are looking to demonstrate the following aspects: |
| − | *To show the tradeoff between sensitivity and specificity; | + | *To show the tradeoff between [[SMHS_PowerSensitivitySpecificity|sensitivity and specificity]]; |
*The closer the curve follows the left-hand border and top border of ROC space, the more accurate is the test; | *The closer the curve follows the left-hand border and top border of ROC space, the more accurate is the test; | ||
*The closer the curve comes to the 45-degree diagonal, the less accurate is the test; | *The closer the curve comes to the 45-degree diagonal, the less accurate is the test; | ||
*The slope of the tangent line at a cut-point gives the likelihood ratio for the value of the test; | *The slope of the tangent line at a cut-point gives the likelihood ratio for the value of the test; | ||
| − | *The area under the curve is a measure of | + | *The area under the curve is a measure of test accuracy. |
| + | [[SMHS_PowerSensitivitySpecificity#Type_I_Error.2C_Type_II_Error_and_Power| Also, see the SMHS Type I and Type II error section]]. | ||
| + | |||
<center> | <center> | ||
{|class="wikitable" style="text-align:center; width:75%" border="1" | {|class="wikitable" style="text-align:center; width:75%" border="1" | ||
| Line 17: | Line 19: | ||
|colspan=2 rowspan=2| ||colspan=2|Actual condition | |colspan=2 rowspan=2| ||colspan=2|Actual condition | ||
|- | |- | ||
| − | |Absent (H_0 is true)||Present (H_1 is true) | + | |Absent ($H_0$ is true)||Present ($H_1$ is true) |
|- | |- | ||
| − | |rowspan=2|Test Result||Negative (fail to reject H_0)||Condition absent + Negative result = True (accurate) Negative (TN, 0.98505)||Condition present + Negative result = False (invalid) Negative (FN, 0.00025)Type II error (β) | + | |rowspan=2|Test Result||Negative (fail to reject $H_0$)||Condition absent + Negative result = True (accurate) Negative (TN, 0.98505)||Condition present + Negative result = False (invalid) Negative (FN, 0.00025)Type II error (β) |
|- | |- | ||
| − | |Positive||(reject H_0) Condition absent + Positive result = False Positive (FP, 0.00995) Type I error (α)||Condition Present + Positive result = True Positive (TP, 0.00475) | + | |Positive||(reject $H_0$) Condition absent + Positive result = False Positive (FP, 0.00995) Type I error (α)||Condition Present + Positive result = True Positive (TP, 0.00475) |
|- | |- | ||
|Test Interpretation||Power = 1-FN=1-0.00025 = 0.99975||Specificity: TN/(TN+FP) =0.98505/(0.98505+0.00995) = 0.99||Sensitivity: TP/(TP+FN) =0.00475/(0.00475+ 0.00025)= 0.95 | |Test Interpretation||Power = 1-FN=1-0.00025 = 0.99975||Specificity: TN/(TN+FP) =0.98505/(0.98505+0.00995) = 0.99||Sensitivity: TP/(TP+FN) =0.00475/(0.00475+ 0.00025)= 0.95 | ||
|} | |} | ||
| − | </center> | + | </center> |
===Theory=== | ===Theory=== | ||
| Line 46: | Line 48: | ||
|} | |} | ||
</center> | </center> | ||
| + | |||
| + | * '''Caution''': The ROC curve is a powerful technique as each individual point on the curve represents an improper scoring rule that is optimized by fitting an inappropriate model. ( The area under the ROC curve (AUC) is a linear translation of the Wilcoxon-Mann-Whitney- rank correlation statistics. Using the ROC curve to identify thresholds may be a low-precision and somewhat arbitrary operation, which may not replicate well from one study to the next. A specific potential problem with over-reliance on the ROC curve may be that it tempts analysts to always identify thresholds for binary test-classification even if such hard-thresholds do not really exist. The field of decision theory may provide more reliable protocols for segmenting, clustering of classifying cases into groups or categories. | ||
====Introduction of ROC Curve==== | ====Introduction of ROC Curve==== | ||
| − | [[SMHS_PowerSensitivitySpecificity|Sensitivity and specificity]] are both characteristics of a test but they also depend on the definition of what constitutes an abnormal test. Consider a medical test | + | [[SMHS_PowerSensitivitySpecificity|Sensitivity and specificity]] are both characteristics of a test but they also depend on the definition of what constitutes an abnormal test. Consider a diagnostic medical test where the cut-points would without doubt influence the test results. We can use the hypothyroidism data from the likelihood ratio to illustrate how these two characteristics change depending on the choice of T4 level that defines hypothyroidism. Recall the data where patients with suspected hypothyroidism are reported. |
<center> | <center> | ||
{|class="wikitable" style="text-align:center; width:75%" border="1" | {|class="wikitable" style="text-align:center; width:75%" border="1" | ||
| Line 79: | Line 83: | ||
| − | Suppose that patients with T4 of 5 or less are considered to be hypothyroid, then the data would be displayed as the following and the sensitivity is 0.56 and specificity is 0.99 in this case. | + | Suppose that patients with T4 of 5 or less are considered to be hypothyroid, then the data would be displayed as the following and the sensitivity ($TP/(TP+FN) =18/32$) is 0.56 and specificity ($TN/(TN+FP)=92/93$) is 0.99 in this case. |
<center> | <center> | ||
{|class="wikitable" style="text-align:center; width:75%" border="1" | {|class="wikitable" style="text-align:center; width:75%" border="1" | ||
| Line 135: | Line 139: | ||
{|class="wikitable" style="text-align:center; width:75%" border="1" | {|class="wikitable" style="text-align:center; width:75%" border="1" | ||
|- | |- | ||
| − | |Cut points||True | + | |Cut points||Rate of True Positives|| Rate of False Positives |
|- | |- | ||
|5||0.56||0.01 | |5||0.56||0.01 | ||
| Line 145: | Line 149: | ||
</center> | </center> | ||
| − | + | Plotting the sensitivity vs. (1-specificity), we get the ROC curve: | |
x<-c(0,0.01,0.19,0.4,0.58,1) | x<-c(0,0.01,0.19,0.4,0.58,1) | ||
y<-c(0,0.56,0.78,0.81,0.91,1) | y<-c(0,0.56,0.78,0.81,0.91,1) | ||
| − | plot(x,y,type='o',main='ROC curve for T4',xlab='False positive rate (specificity)',ylab='True positive rate (sensitivity)') | + | plot(x,y,type='o',main='ROC curve for T4',xlab='False positive rate (1-specificity)',ylab='True positive rate (sensitivity)') |
| + | |||
| + | install.packages("pROC") | ||
| + | library("pROC") | ||
| + | HypothyroidResponse <- c(2,3,1,8,4,4,3,3,1,0,2,1,0) | ||
| + | PredictorThreshold <- c('poor','good','good','poor','good','poor','poor','poor','good','good','poor','good','good') | ||
| + | # Syntax (response, predictor) | ||
| + | auc(factor(PredictorThreshold), HypothyroidResponse) | ||
| + | # the AUC=P(random positive example > random negative example) | ||
| + | |||
| + | > Area under the curve: 0.8214 | ||
| + | |||
<center> | <center> | ||
| − | [[File:ROC Fig 1.png]] | + | [[File:ROC Fig 1.png|500px]] |
</center> | </center> | ||
| Line 163: | Line 178: | ||
*Computing ROC: The calculation protocol of the area under the ROC curve is important. The area measures discrimination, which is the ability of the test to correctly classify those with and without the disease. The area under the curve is the percentage of randomly drawn pairs for which this is true. Two methods are commonly used to calculate the area of the scope: | *Computing ROC: The calculation protocol of the area under the ROC curve is important. The area measures discrimination, which is the ability of the test to correctly classify those with and without the disease. The area under the curve is the percentage of randomly drawn pairs for which this is true. Two methods are commonly used to calculate the area of the scope: | ||
:: non-parametric method based on constructing trapezoids under the curve as approximation of area; | :: non-parametric method based on constructing trapezoids under the curve as approximation of area; | ||
| − | :: a parametric method using a [[SMHS_CIs#Maximum_likelihood_estimation_.28MLE.29|MLE | + | :: a parametric method using a [[SMHS_CIs#Maximum_likelihood_estimation_.28MLE.29|MLE]] to fit a smooth curve to data points. |
===Applications=== | ===Applications=== | ||
| − | [http://pubs.rsna.org/doi/abs/10.1148/radiology.143.1.7063747 This article] titled The Meaning And the Use Of The Area Under A Receiver Operating Characteristic (ROC) Curve presented a representation and interpretation of the area under a ROC curve obtained by the ‘rating’ method, or by mathematical predictions based on patient characteristics. It showed that that in such a setting the area represents the probability that a randomly chosen diseased subject is (correctly) rated or ranked with greater suspicion than a randomly chosen non-diseased subject. | + | We can use the [[SOCR_Data_July2009_ID_NI#Curvedness_Data|smaller summary Alzheimer's disease (AD) dataset of Global Gray Matter Volume (GMV) and Cortical Surface Curvedness morphometry measures]] to illustrate the concepts of false-positive, false-negative, sensitivity, specificity and power of a test. |
| + | |||
| + | Suppose we try to determine the ''best'' threshold of the GMV or the curvedness (a measure of cortical surface smoothness) that can be used as a test for AD. We would combine NC+MCI and explore the effects of varying the GMV threshold on the false-positive and false-negative rates. The table below uses these simple formulas to compute the number of false-positive ($=COUNTIF(GMVCurvednessTable!GMV29:GMV105, "<="\&A2)$, count non-AD cases with GMV$\le$threshold) and false-negative ($=COUNTIF(GMVCurvednessTable!GMV2:GMV28, ">"\&A2)$, count AD cases with GMV>threshold) frequencies for each threshold between $35\times 10^4$ and $75\times 10^4$ (in increments of $20,000$). | ||
| + | |||
| + | <center> | ||
| + | {| class="wikitable" style="text-align:center;" border="2" | ||
| + | |- | ||
| + | ! Threshold||AD_Test_GMV<Threshold_FalsePositives||FalseNegatives | ||
| + | |- | ||
| + | |350000||0||26 | ||
| + | |- | ||
| + | |370000||0||26 | ||
| + | |- | ||
| + | |390000||1||25 | ||
| + | |- | ||
| + | |410000||3||23 | ||
| + | |- | ||
| + | |430000||5||23 | ||
| + | |- | ||
| + | |450000||7||23 | ||
| + | |- | ||
| + | |470000||11||20 | ||
| + | |- | ||
| + | |490000||23||18 | ||
| + | |- | ||
| + | |510000||39||15 | ||
| + | |- | ||
| + | |530000||47||13 | ||
| + | |- | ||
| + | |550000||56||13 | ||
| + | |- | ||
| + | |570000||64||13 | ||
| + | |- | ||
| + | |590000||68||12 | ||
| + | |- | ||
| + | |610000||70||8 | ||
| + | |- | ||
| + | |630000||71||7 | ||
| + | |- | ||
| + | |650000||75||7 | ||
| + | |- | ||
| + | |670000||76||5 | ||
| + | |- | ||
| + | |690000||76||3 | ||
| + | |- | ||
| + | |710000||77||2 | ||
| + | |- | ||
| + | |730000||77||1 | ||
| + | |- | ||
| + | |750000||77||0 | ||
| + | |} | ||
| + | </center> | ||
| + | |||
| + | The figure below illustrates graphically the effect of increasing the GMV threshold (binary classification of cases into AD group or NC+MCI group) on the false-positive (red) and false-negative (blue) classification rates. | ||
| + | <center> | ||
| + | [[Image:SMHS_ROC_Fig10.png|600px]] | ||
| + | </center> | ||
| + | |||
| + | We can use a similar R-script to compute the number of: | ||
| + | * false-positive, counting non-AD cases with GMV ≤ threshold, and | ||
| + | * false-negative, counting AD cases with GMV > threshold, for each threshold between $35×10^4$ and $75×10^4$ (in increments of $20,000$). | ||
| + | |||
| + | First save the table: [[SOCR_Data_July2009_ID_NI#Curvedness_Data| Alzheimer's disease (AD) dataset of Global Gray Matter Volume (GMV) and Cortical Surface Curvedness morphometry measures]], as CSV file (C:\User\GMV.csv) on your hard-drive. | ||
| + | |||
| + | dataset <- read.csv('C:\\User\\GMV.csv') | ||
| + | attach(dataset) | ||
| + | summary(GMV) | ||
| + | nonAD <- subset(dataset,Group!='AD') | ||
| + | threshold <- seq(350000,750000,by=20000) | ||
| + | calculate <- function(thres) | ||
| + | { | ||
| + | false.p <- sum(as.numeric(nonAD$\$ $GMV<=thres)) | ||
| + | false.n <- sum(as.numeric(nonAD$\$ $GMV>thres)) | ||
| + | cnt <- c(false.p,false.n) | ||
| + | return(cnt) | ||
| + | } | ||
| + | result_FP_FN <- apply(as.matrix(threshold,,1),1,calculate) | ||
| + | rownames(result_FP_FN) <- c('False Positive','False Negative') | ||
| + | colnames(result_FP_FN) <- c(as.character(threshold)) | ||
| + | result_FP_FN | ||
| + | threshold | ||
| + | # result_FP_FN[,4] # 4th column of matrix | ||
| + | # result_FP_FN[3,] # 3rd row of matrix | ||
| + | # result_FP_FN[2:4,1:5] # rows 2,3,4 of columns 1,2,3,4,5 | ||
| + | result_FP_FN[1,] | ||
| + | result_FP_FN[2,] | ||
| + | |||
| + | # transpose and print the FP_FN matrix | ||
| + | t(result_FP_FN) | ||
| + | |||
| + | We can dig a bit deeper by plotting the impact of thresholding the global GMV on the false-positive (FP) and false-negative (FN) rates. The R-script below generates this figure, where the thresholds ($\times 10^4$) are used as labels for each point in the FP vs. FN scatter plot. If committing FN errors is $R$ times more expensive than committing FP errors, then the '''best operating point''' (hence ROC) will be tangent to the FP-FN curve/line with a slope of $-R$. Therefore, if $R=\frac{1}{8}$, we should set the threshold to 53 (as the slope of the green line will be $\frac{13-14}{48-40}=-\frac{1}{8}$) and if $R=2$, the threshold should be 41 (as the slope of the purple line will be $\frac{23-25}{3-2}=-\frac{2}{1}=-2$): | ||
| + | |||
| + | par(mfrow = c(1,1)) | ||
| + | |||
| + | leg.txt <- c("FP vs. FN", "Thresholds", "Line Slope=-1/8", "Line Slope = -2") | ||
| + | |||
| + | Threshold <- c(35,37,39,41,43,45,47,49,51,53,55,57,59,61,63,65,67,69,71,73,75) | ||
| + | FalsePositives <-c(0,0,1,3,5,7,11,23,39,47,56,64,68,70,71,75,76,76,77,77,77) | ||
| + | FalseNegatives <- c(26,26,25,23,23,23,20,18,15,13,13,13,12,8,7,7,5,3,2,1,0) | ||
| + | plot(FalsePositives, FalseNegatives, type="b", pch=21, col="red", lty=1, | ||
| + | xlab="False-Positives", ylab="FalseNegatives", | ||
| + | main = "Impact of Thresholding the Global GMV on the FP vs. FN") | ||
| + | |||
| + | linex1 <- c(40, 48) | ||
| + | liney1 <- c(14, 13) | ||
| + | linez1 <- lm(liney1 ~linex1) | ||
| + | abline (linez1, col="green") | ||
| + | linex2 <- c(3, 2) | ||
| + | liney2 <- c(23, 25) | ||
| + | linez2 <- lm(liney2 ~linex2) | ||
| + | abline (linez2, col="purple") | ||
| + | # lines(linex2, liney2, ol=" purple ",lwd=2.5) | ||
| + | |||
| + | text(FalsePositives, FalseNegatives, Threshold, cex=0.6, pos=1, col="blue") | ||
| + | legend(list(x = 58,y = 29), legend = leg.txt, col=c("red", "blue", "green", "purple"), | ||
| + | #col = c(1,3,1,2), | ||
| + | lty = 1, merge = TRUE) | ||
| + | |||
| + | <center> | ||
| + | [[Image:SMHS_ROC_Fig11.png|600px]] | ||
| + | </center> | ||
| + | |||
| + | ====R AUC/ROC Example==== | ||
| + | Below is an example using the ROCR R-package to generate the ROC curve and compute the AUC. First download the data table: [[SOCR_Data_July2009_ID_NI#Curvedness_Data|Alzheimer's disease (AD) dataset of Global Gray Matter Volume (GMV) and Cortical Surface Curvedness morphometry measures]], as CSV file (C:\User\GMV.csv) on your hard-drive. | ||
| + | |||
| + | # Install and load the necessary packages | ||
| + | # in this case: RandomForest classifier and the ROCR for visualization and scoring of classifiers | ||
| + | #install.packages("randomForest") | ||
| + | library("randomForest") | ||
| + | library("ROCR") # load the ROCR package containing the performance method | ||
| + | |||
| + | dataset <- read.csv('C:\\Users\\GMV.csv') | ||
| + | attach(dataset) #to ensure all variables/data elements are directly accessible in the R-session | ||
| + | # remove the TBV, or any other variable | ||
| + | # subset(dataset, select=-c(TBV)) | ||
| + | # train the random forest model | ||
| + | # if you need to remove some cases/rows - example, binarize the classes | ||
| + | # For instance, ROCR currently supports only evaluation of binary classification tasks. | ||
| + | dataset <- dataset[(dataset$\$ $Group != "MCI"),] | ||
| + | dataset$\$ $Group <- factor(dataset$\$ $Group) | ||
| + | |||
| + | AD.rf <-randomForest(Group ~ MMSE+CDR+Sex+Age+TBV+GMV+WMV+CSFV+Curvedness, ntree=100, keep.forest=TRUE, importance=TRUE) | ||
| + | AD.rf.predict <- predict(AD.rf, dataset, type="prob")[,2] | ||
| + | |||
| + | plot(performance(prediction(AD.rf.predict, dataset$\$ $Group),"tpr","fpr"),col = "blue") | ||
| + | auc_RF <- performance(prediction(AD.rf.predict, dataset$\$ $Group),"auc")$@y.values[[1]]$ | ||
| + | legend("topleft",legend=c(paste( | ||
| + | "Random Forest Prediction Model (AUC=",formatC(auc_RF,digits=4,format="f"), | ||
| + | ")",sep="")), col=c("blue"), lty=1) | ||
| + | abline(a=0,b=1,lwd=2,lty=2,col="gray") | ||
| + | |||
| + | [[Image:SMHS_ROC_Fig14.png|600px]] | ||
| + | |||
| + | # General Model: fit <- glm(Group~., dataset, family=binomial) | ||
| + | fitGLM <- glm(Group~ GMV + WMV, dataset, family=binomial) | ||
| + | # predict the linear model fit using the real data | ||
| + | train.predictGLM <- predict(fitGLM, newdata = dataset, type="response") | ||
| + | library(ROCR) | ||
| + | plot(performance(prediction(train.predictGLM, dataset$\$ $Group),"tpr","fpr"),col = "red") | ||
| + | auc_value <- performance(prediction(train.predictGLM, dataset$\$ $Group),"auc")$@y.values[[1]]$ | ||
| + | legend("bottomright",legend=c(paste( | ||
| + | "Logistic Regression Model Fit(AUC=",formatC(auc_value,digits=4,format="f"), | ||
| + | ")",sep="")), col=c("red"), lty=1) | ||
| + | abline(a=0,b=1,lwd=2,lty=2,col="gray") | ||
| + | [[Image:SMHS_ROC_Fig15.png|600px]] | ||
| + | |||
| + | : Note that in this case we only illustrated the ROC curve construction for the GMV variable, however similar analyses can be done for some of the [[SOCR_Data_July2009_ID_NI#Curvedness_Data|other variables in this dataset (e.g., MMSE, CDR, TBV, GMV, WMV, CSFV, Curvedness)]]. | ||
| + | |||
| + | * [http://pubs.rsna.org/doi/abs/10.1148/radiology.143.1.7063747 This article] titled The Meaning And the Use Of The Area Under A Receiver Operating Characteristic (ROC) Curve presented a representation and interpretation of the area under a ROC curve obtained by the ‘rating’ method, or by mathematical predictions based on patient characteristics. It showed that that in such a setting the area represents the probability that a randomly chosen diseased subject is (correctly) rated or ranked with greater suspicion than a randomly chosen non-diseased subject. | ||
| − | [http://www.sciencedirect.com/science/article/pii/S0001299878800142 This article] illustrated practical experimental techniques for measuring ROC curves and discussed about the issues of case selection and curve-fitting. It also talked about possible generalizations of conventional ROC analysis to account for decision performance in complex diagnostic tasks and showed ROC analysis related in direct and natural way to cost/benefit analysis of diagnostic decision making. This paper developed the concepts of ‘average diagnostic cost’ and ‘average net benefit’ to identify the optimal compromise among various kinds of diagnostic error and suggested ways in ROC analysis to optimize diagnostic strategies. | + | * [http://www.sciencedirect.com/science/article/pii/S0001299878800142 This article] illustrated practical experimental techniques for measuring ROC curves and discussed about the issues of case selection and curve-fitting. It also talked about possible generalizations of conventional ROC analysis to account for decision performance in complex diagnostic tasks and showed ROC analysis related in direct and natural way to cost/benefit analysis of diagnostic decision making. This paper developed the concepts of ‘average diagnostic cost’ and ‘average net benefit’ to identify the optimal compromise among various kinds of diagnostic error and suggested ways in ROC analysis to optimize diagnostic strategies. |
===Software=== | ===Software=== | ||
Latest revision as of 13:21, 23 November 2014
Contents
Scientific Methods for Health Sciences - Receiver Operating Characteristic (ROC) Curve
Overview
Receiver operating characteristic (ROC curve) is a graphical plot, which illustrates the performance of a binary classifier system as its discrimination threshold varies. The ROC curve is created by plotting the fraction of true positive out of the total actual positives vs. the fraction of false positives out of the total actual negatives at various threshold settings. In this section, we are going to introduce the ROC curve and illustrate applications of this method with examples.
Motivation
We have talked about the cases with a binary classification where the outcomes are either absent or present and the test results are positive or negative. We have also previously discussed sensitivity and specificity which are associated with the concepts of true positive and true negatives. With ROC curve, we are looking to demonstrate the following aspects:
- To show the tradeoff between sensitivity and specificity;
- The closer the curve follows the left-hand border and top border of ROC space, the more accurate is the test;
- The closer the curve comes to the 45-degree diagonal, the less accurate is the test;
- The slope of the tangent line at a cut-point gives the likelihood ratio for the value of the test;
- The area under the curve is a measure of test accuracy.
Also, see the SMHS Type I and Type II error section.
| Actual condition | |||
| Absent ($H_0$ is true) | Present ($H_1$ is true) | ||
| Test Result | Negative (fail to reject $H_0$) | Condition absent + Negative result = True (accurate) Negative (TN, 0.98505) | Condition present + Negative result = False (invalid) Negative (FN, 0.00025)Type II error (β) |
| Positive | (reject $H_0$) Condition absent + Positive result = False Positive (FP, 0.00995) Type I error (α) | Condition Present + Positive result = True Positive (TP, 0.00475) | |
| Test Interpretation | Power = 1-FN=1-0.00025 = 0.99975 | Specificity: TN/(TN+FP) =0.98505/(0.98505+0.00995) = 0.99 | Sensitivity: TP/(TP+FN) =0.00475/(0.00475+ 0.00025)= 0.95 |
Theory
Review of basic concepts in a binary classification:
| Disease Status | Metrics | ||||
| Disease | No Disease | Prevalence=$\frac{\sum Condition\, positive}{\sum Total\, population}$ | |||
| Screening Test | Positive | a (True positives) | b (False positives) | Positive predictive value (PPV)=$\frac{\sum Ture\, positive}{\sum Test\,positives}$ | False discovery rate (FDR)=$\frac{\sum False\, positive}{\sum Test\, positive}$ |
| Negative | c (False negatives) | d (True negatives) | False omission rate (FOR)=$\frac{\sum False\, negative} {\sum Test\, negative}$ | Negative predictive value (NPV)=$\frac{\sum True\, negative}{\sum Test\, negative}$ | |
| Positive Likelihood Ratio=TPR/FBR | True positive rate (TPR)=$\frac{\sum True\, positive} {\sum Condition\, positive}$ | False positive rate (FPR)=$\frac{\sum False\, positive}{\sum Condition\, positive}$ | |||
| Negative Likelihood Ratio=FNR/TNR | False negative rate (FNR)=$\frac{\sum False\, negative} {\sum condition\, negative}$ | True negative rate (TNR)=$\frac{\sum True\, negative}{\sum Condition\, negative}$ | |||
- Caution: The ROC curve is a powerful technique as each individual point on the curve represents an improper scoring rule that is optimized by fitting an inappropriate model. ( The area under the ROC curve (AUC) is a linear translation of the Wilcoxon-Mann-Whitney- rank correlation statistics. Using the ROC curve to identify thresholds may be a low-precision and somewhat arbitrary operation, which may not replicate well from one study to the next. A specific potential problem with over-reliance on the ROC curve may be that it tempts analysts to always identify thresholds for binary test-classification even if such hard-thresholds do not really exist. The field of decision theory may provide more reliable protocols for segmenting, clustering of classifying cases into groups or categories.
Introduction of ROC Curve
Sensitivity and specificity are both characteristics of a test but they also depend on the definition of what constitutes an abnormal test. Consider a diagnostic medical test where the cut-points would without doubt influence the test results. We can use the hypothyroidism data from the likelihood ratio to illustrate how these two characteristics change depending on the choice of T4 level that defines hypothyroidism. Recall the data where patients with suspected hypothyroidism are reported.
| T4 | <1 | 1-2 | 2-3 | 3-4 | 4-5 | 5-6 | 6-7 | 7-8 | 8-9 | 9-10 | 10-11 | 11-12 | >12 |
| Hypothyroid | 2 | 3 | 1 | 8 | 4 | 4 | 3 | 3 | 1 | 0 | 2 | 1 | 0 |
| Euthyroid | 0 | 0 | 0 | 0 | 1 | 6 | 11 | 19 | 17 | 20 | 11 | 4 | 4 |
With the following cut-points, we have the data listed:
| T4 value | Hypothyroid | Euthyroid |
| 5 or less | 18 | 1 |
| 5.1 - 7 | 7 | 17 |
| 7.1 - 9 | 4 | 36 |
| 9 or more | 3 | 39 |
| Totals: | 32 | 93 |
Suppose that patients with T4 of 5 or less are considered to be hypothyroid, then the data would be displayed as the following and the sensitivity ($TP/(TP+FN) =18/32$) is 0.56 and specificity ($TN/(TN+FP)=92/93$) is 0.99 in this case.
| T4 value | Hypothyroid | Euthyroid |
| 5 or less | 18 | 1 |
| More than 5 | 14 | 92 |
| Totals: | 32 | 93 |
Now suppose, we decided to be less stringent on the disease and consider the patients with T4 values of 7 or less to be hypothyroid, then the data would be recorded as the following and the sensitivity in this case would be 0.78 and specificity 0.81:
| T4 value | Hypothyroid | Euthyroid |
| 7 or less | 25 | 18 |
| More than 7 | 7 | 75 |
| Totals: | 32 | 93 |
If we move the cut-point for hypothyroidism a little bit higher, say 9, we would have the sensitivity of 0.91 and specificity 0.42:
| T4 value | Hypothyroid | Euthyroid |
| 9 or less | 29 | 54 |
| More than 9 | 3 | 39 |
| Totals: | 32 | 93 |
To sum up, we have the pairs of sensitivity an specificity with corresponding cut-points in the following table:
| Cut points | Sensitivity | Specificity |
| 5 | 0.56 | 0.99 |
| 7 | 0.78 | 0.81 |
| 9 | 0.91 | 0.42 |
From the table above, we observe that the sensitivity improves with increasing cut-point T4 value while specificity increases with decreasing cut-point T4 value. That is a tradeoff between sensitivity and specificity. The table above can also be shown as TP and FP.
| Cut points | Rate of True Positives | Rate of False Positives |
| 5 | 0.56 | 0.01 |
| 7 | 0.78 | 0.19 |
| 9 | 0.91 | 0.58 |
Plotting the sensitivity vs. (1-specificity), we get the ROC curve:
x<-c(0,0.01,0.19,0.4,0.58,1)
y<-c(0,0.56,0.78,0.81,0.91,1)
plot(x,y,type='o',main='ROC curve for T4',xlab='False positive rate (1-specificity)',ylab='True positive rate (sensitivity)')
install.packages("pROC")
library("pROC")
HypothyroidResponse <- c(2,3,1,8,4,4,3,3,1,0,2,1,0)
PredictorThreshold <- c('poor','good','good','poor','good','poor','poor','poor','good','good','poor','good','good')
# Syntax (response, predictor)
auc(factor(PredictorThreshold), HypothyroidResponse)
# the AUC=P(random positive example > random negative example)
> Area under the curve: 0.8214
- ROC interpretation: The area under the ROC Curve can be used to classify the accuracy of a diagnostic test according to the following academic point system:
- 0.90-1: excellent;
- 0.8-0.9: good;
- 0.7-0.8: fair;
- 0.6-0.7: poor;
- 0.5-0.7:fail.
With our example above, the area under the T4 ROC curve is 0.86, which shows that the accuracy of the test is good in separating hypothyroid from euthyroid patients.
- Computing ROC: The calculation protocol of the area under the ROC curve is important. The area measures discrimination, which is the ability of the test to correctly classify those with and without the disease. The area under the curve is the percentage of randomly drawn pairs for which this is true. Two methods are commonly used to calculate the area of the scope:
- non-parametric method based on constructing trapezoids under the curve as approximation of area;
- a parametric method using a MLE to fit a smooth curve to data points.
Applications
We can use the smaller summary Alzheimer's disease (AD) dataset of Global Gray Matter Volume (GMV) and Cortical Surface Curvedness morphometry measures to illustrate the concepts of false-positive, false-negative, sensitivity, specificity and power of a test.
Suppose we try to determine the best threshold of the GMV or the curvedness (a measure of cortical surface smoothness) that can be used as a test for AD. We would combine NC+MCI and explore the effects of varying the GMV threshold on the false-positive and false-negative rates. The table below uses these simple formulas to compute the number of false-positive ($=COUNTIF(GMVCurvednessTable!GMV29:GMV105, "<="\&A2)$, count non-AD cases with GMV$\le$threshold) and false-negative ($=COUNTIF(GMVCurvednessTable!GMV2:GMV28, ">"\&A2)$, count AD cases with GMV>threshold) frequencies for each threshold between $35\times 10^4$ and $75\times 10^4$ (in increments of $20,000$).
| Threshold | AD_Test_GMV<Threshold_FalsePositives | FalseNegatives |
|---|---|---|
| 350000 | 0 | 26 |
| 370000 | 0 | 26 |
| 390000 | 1 | 25 |
| 410000 | 3 | 23 |
| 430000 | 5 | 23 |
| 450000 | 7 | 23 |
| 470000 | 11 | 20 |
| 490000 | 23 | 18 |
| 510000 | 39 | 15 |
| 530000 | 47 | 13 |
| 550000 | 56 | 13 |
| 570000 | 64 | 13 |
| 590000 | 68 | 12 |
| 610000 | 70 | 8 |
| 630000 | 71 | 7 |
| 650000 | 75 | 7 |
| 670000 | 76 | 5 |
| 690000 | 76 | 3 |
| 710000 | 77 | 2 |
| 730000 | 77 | 1 |
| 750000 | 77 | 0 |
The figure below illustrates graphically the effect of increasing the GMV threshold (binary classification of cases into AD group or NC+MCI group) on the false-positive (red) and false-negative (blue) classification rates.
We can use a similar R-script to compute the number of:
- false-positive, counting non-AD cases with GMV ≤ threshold, and
- false-negative, counting AD cases with GMV > threshold, for each threshold between $35×10^4$ and $75×10^4$ (in increments of $20,000$).
First save the table: Alzheimer's disease (AD) dataset of Global Gray Matter Volume (GMV) and Cortical Surface Curvedness morphometry measures, as CSV file (C:\User\GMV.csv) on your hard-drive.
dataset <- read.csv('C:\\User\\GMV.csv')
attach(dataset)
summary(GMV)
nonAD <- subset(dataset,Group!='AD')
threshold <- seq(350000,750000,by=20000)
calculate <- function(thres)
{
false.p <- sum(as.numeric(nonAD$\$ $GMV<=thres))
false.n <- sum(as.numeric(nonAD$\$ $GMV>thres))
cnt <- c(false.p,false.n)
return(cnt)
}
result_FP_FN <- apply(as.matrix(threshold,,1),1,calculate)
rownames(result_FP_FN) <- c('False Positive','False Negative')
colnames(result_FP_FN) <- c(as.character(threshold))
result_FP_FN
threshold
# result_FP_FN[,4] # 4th column of matrix
# result_FP_FN[3,] # 3rd row of matrix
# result_FP_FN[2:4,1:5] # rows 2,3,4 of columns 1,2,3,4,5
result_FP_FN[1,]
result_FP_FN[2,]
# transpose and print the FP_FN matrix
t(result_FP_FN)
We can dig a bit deeper by plotting the impact of thresholding the global GMV on the false-positive (FP) and false-negative (FN) rates. The R-script below generates this figure, where the thresholds ($\times 10^4$) are used as labels for each point in the FP vs. FN scatter plot. If committing FN errors is $R$ times more expensive than committing FP errors, then the best operating point (hence ROC) will be tangent to the FP-FN curve/line with a slope of $-R$. Therefore, if $R=\frac{1}{8}$, we should set the threshold to 53 (as the slope of the green line will be $\frac{13-14}{48-40}=-\frac{1}{8}$) and if $R=2$, the threshold should be 41 (as the slope of the purple line will be $\frac{23-25}{3-2}=-\frac{2}{1}=-2$):
par(mfrow = c(1,1))
leg.txt <- c("FP vs. FN", "Thresholds", "Line Slope=-1/8", "Line Slope = -2")
Threshold <- c(35,37,39,41,43,45,47,49,51,53,55,57,59,61,63,65,67,69,71,73,75)
FalsePositives <-c(0,0,1,3,5,7,11,23,39,47,56,64,68,70,71,75,76,76,77,77,77)
FalseNegatives <- c(26,26,25,23,23,23,20,18,15,13,13,13,12,8,7,7,5,3,2,1,0)
plot(FalsePositives, FalseNegatives, type="b", pch=21, col="red", lty=1,
xlab="False-Positives", ylab="FalseNegatives",
main = "Impact of Thresholding the Global GMV on the FP vs. FN")
linex1 <- c(40, 48)
liney1 <- c(14, 13)
linez1 <- lm(liney1 ~linex1)
abline (linez1, col="green")
linex2 <- c(3, 2)
liney2 <- c(23, 25)
linez2 <- lm(liney2 ~linex2)
abline (linez2, col="purple")
# lines(linex2, liney2, ol=" purple ",lwd=2.5)
text(FalsePositives, FalseNegatives, Threshold, cex=0.6, pos=1, col="blue")
legend(list(x = 58,y = 29), legend = leg.txt, col=c("red", "blue", "green", "purple"),
#col = c(1,3,1,2),
lty = 1, merge = TRUE)
R AUC/ROC Example
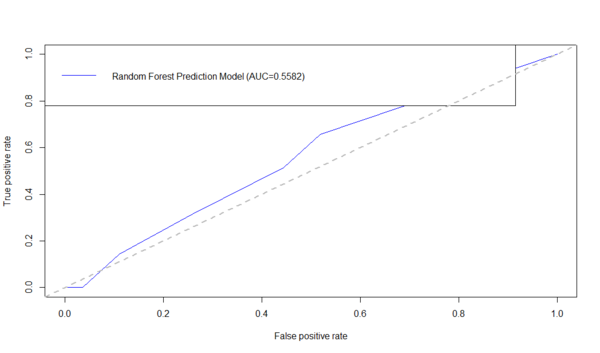
Below is an example using the ROCR R-package to generate the ROC curve and compute the AUC. First download the data table: Alzheimer's disease (AD) dataset of Global Gray Matter Volume (GMV) and Cortical Surface Curvedness morphometry measures, as CSV file (C:\User\GMV.csv) on your hard-drive.
# Install and load the necessary packages
# in this case: RandomForest classifier and the ROCR for visualization and scoring of classifiers
#install.packages("randomForest")
library("randomForest")
library("ROCR") # load the ROCR package containing the performance method
dataset <- read.csv('C:\\Users\\GMV.csv')
attach(dataset) #to ensure all variables/data elements are directly accessible in the R-session
# remove the TBV, or any other variable
# subset(dataset, select=-c(TBV))
# train the random forest model
# if you need to remove some cases/rows - example, binarize the classes
# For instance, ROCR currently supports only evaluation of binary classification tasks.
dataset <- dataset[(dataset$\$ $Group != "MCI"),]
dataset$\$ $Group <- factor(dataset$\$ $Group)
AD.rf <-randomForest(Group ~ MMSE+CDR+Sex+Age+TBV+GMV+WMV+CSFV+Curvedness, ntree=100, keep.forest=TRUE, importance=TRUE) AD.rf.predict <- predict(AD.rf, dataset, type="prob")[,2] plot(performance(prediction(AD.rf.predict, dataset$\$ $Group),"tpr","fpr"),col = "blue") auc_RF <- performance(prediction(AD.rf.predict, dataset$\$ $Group),"auc")$@y.values1$ legend("topleft",legend=c(paste( "Random Forest Prediction Model (AUC=",formatC(auc_RF,digits=4,format="f"), ")",sep="")), col=c("blue"), lty=1) abline(a=0,b=1,lwd=2,lty=2,col="gray")
# General Model: fit <- glm(Group~., dataset, family=binomial) fitGLM <- glm(Group~ GMV + WMV, dataset, family=binomial) # predict the linear model fit using the real data train.predictGLM <- predict(fitGLM, newdata = dataset, type="response") library(ROCR) plot(performance(prediction(train.predictGLM, dataset$\$ $Group),"tpr","fpr"),col = "red") auc_value <- performance(prediction(train.predictGLM, dataset$\$ $Group),"auc")$@y.values1$ legend("bottomright",legend=c(paste( "Logistic Regression Model Fit(AUC=",formatC(auc_value,digits=4,format="f"), ")",sep="")), col=c("red"), lty=1) abline(a=0,b=1,lwd=2,lty=2,col="gray")
- Note that in this case we only illustrated the ROC curve construction for the GMV variable, however similar analyses can be done for some of the other variables in this dataset (e.g., MMSE, CDR, TBV, GMV, WMV, CSFV, Curvedness).
- This article titled The Meaning And the Use Of The Area Under A Receiver Operating Characteristic (ROC) Curve presented a representation and interpretation of the area under a ROC curve obtained by the ‘rating’ method, or by mathematical predictions based on patient characteristics. It showed that that in such a setting the area represents the probability that a randomly chosen diseased subject is (correctly) rated or ranked with greater suspicion than a randomly chosen non-diseased subject.
- This article illustrated practical experimental techniques for measuring ROC curves and discussed about the issues of case selection and curve-fitting. It also talked about possible generalizations of conventional ROC analysis to account for decision performance in complex diagnostic tasks and showed ROC analysis related in direct and natural way to cost/benefit analysis of diagnostic decision making. This paper developed the concepts of ‘average diagnostic cost’ and ‘average net benefit’ to identify the optimal compromise among various kinds of diagnostic error and suggested ways in ROC analysis to optimize diagnostic strategies.
Software
# With the given example in R: x<-c(0,0.01,0.19,0.58,1) y<-c(0,0.56,0.78,0.91,1) plot(x,y,type='o',main='ROC curve for T4',xlab='False positive rate (specificity)',ylab='True positive rate (sensitivity)')
Problems
6.1) Suppose that a new study is conducted on lung cancer and the following data is collected in identify between two types of lung cancers (say type a and type b). Conduct the ROC curve for this example by varying the cut-points from 2 to 10 by increasing 2 units each time. Calculate the area under the curve and interpret on the accuracy of the test.
| measurements | <1 | 1-2 | 2-3 | 3-4 | 4-5 | 5-6 | 6-7 | 7-8 | 8-9 | 9-10 | 10-11 | 11-12 | >12 |
| Type a | 2 | 1 | 4 | 2 | 8 | 7 | 4 | 3 | 0 | 0 | 1 | 2 | 2 |
| Type b | 1 | 3 | 0 | 2 | 2 | 5 | 10 | 23 | 18 | 20 | 15 | 8 | 2 |
6.2) When a serious disease can be treated if it is caught early, it is more important to have a test with high specificity than high sensitivity.
a. True
b. False
6.3) The positive predictive value of a test is calculated by dividing the number of:
(a) True positives in the population
(b) True negatives in the population
(c) People who test positive
(d) People who test negative
6.4) A new screening test has been developed for diabetes. The table below represents the results of the new test compared to the current gold standard.
| Condition positive | Condition negative | Total | |
| Test positive | 80 | 70 | 150 |
| Test negative | 10 | 240 | 250 |
| Total | 90 | 310 | 400 |
What is the sensitivity of the test?
(a) 77%
(b) 89%
(c) 80%
(d) 53%
6.5) What is the specificity of the test?
(a) 77%
(b) 89%
(c) 80%
(d) 53%
6.6) What is the positive predictive value of the test?
(a) 77%
(b) 89%
(c) 80%
(d) 53%