Difference between revisions of "SMHS TimeSeriesAnalysis"
(→Auto-regressive Integrated Moving Average (ARIMA) Models4) |
m (Text replacement - "{{translate|pageName=http://wiki.stat.ucla.edu/socr/" to ""{{translate|pageName=http://wiki.socr.umich.edu/") |
||
| (40 intermediate revisions by 3 users not shown) | |||
| Line 2: | Line 2: | ||
===Questions=== | ===Questions=== | ||
| − | |||
* Why are trends, patterns or predictions from models/data important? | * Why are trends, patterns or predictions from models/data important? | ||
* How to detect, model and utilize trends in longitudinal data? | * How to detect, model and utilize trends in longitudinal data? | ||
| Line 12: | Line 11: | ||
There are 3 (distinct and complementary) types of <b>time series patterns</b> that most time-series analyses are trying to identify, model and analyze. These include: | There are 3 (distinct and complementary) types of <b>time series patterns</b> that most time-series analyses are trying to identify, model and analyze. These include: | ||
| − | *<b>Trend</b>: A trend is a long-term increase or decrease in the data that may be linear or non-linear, but is generally continuous (mostly monotonic). The trend may be referred to as direction. | + | * <b>Trend</b>: A trend is a long-term increase or decrease in the data that may be linear or non-linear, but is generally continuous (mostly monotonic). The trend may be referred to as direction. |
| − | + | * <b>Seasonal</b>: A seasonal pattern is influence in the data, like seasonal factors (e.g., the quarter of the year, the month, or day of the week), which is always of a fixed known period. | |
| − | *<b>Seasonal</b>: A seasonal pattern is influence in the data, like seasonal factors (e.g., the quarter of the year, the month, or day of the week), which is always of a fixed known period. | + | * <b>Cyclic</b>: A cyclic pattern of fluctuations corresponds to rises and falls that are <i>not of fixed period.</i> |
| − | |||
| − | *<b>Cyclic</b>: A cyclic pattern of fluctuations corresponds to rises and falls that are <i>not of fixed period.</i> | ||
| − | [[Image:SMHS_TimeSeries1.png|300px]] | + | <center>[[Image:SMHS_TimeSeries1.png|300px]]</center> |
For example, the following code shows several time series with different types of time series patterns. | For example, the following code shows several time series with different types of time series patterns. | ||
| Line 50: | Line 47: | ||
Note: If you get this run-time graphics error: | Note: If you get this run-time graphics error: | ||
| − | “<font color="red">Error in plot.new() : figure margins too large</font>” | + | “<font color="red">Error in plot.new() : figure margins too large</font>” <BR> |
| − | |||
You need to make sure your graphics window is large enough or print to PDF: | You need to make sure your graphics window is large enough or print to PDF: | ||
pdf("myplot.pdf"); plot(x); dev.off() | pdf("myplot.pdf"); plot(x); dev.off() | ||
| − | [[Image:SMHS_TimeSeries2.png|300px]] | + | <center>[[Image:SMHS_TimeSeries2.png|300px]]</center> |
Let’s look at the delta (Δ) changes - Lagged Differences, using <b>diff</b>, which returns suitably lagged and iterated differences. | Let’s look at the delta (Δ) changes - Lagged Differences, using <b>diff</b>, which returns suitably lagged and iterated differences. | ||
| Line 67: | Line 63: | ||
lines(x,y,lwd=2,col="blue") # plot MLE Normal Fit | lines(x,y,lwd=2,col="blue") # plot MLE Normal Fit | ||
| − | + | ===Time series decomposition=== | |
Denote the time series $yt$ including the three components: a seasonal effect, a trend-cycle effect (containing both trend and cycle), and a remainder component (containing the residual variability in the time series). | Denote the time series $yt$ including the three components: a seasonal effect, a trend-cycle effect (containing both trend and cycle), and a remainder component (containing the residual variability in the time series). | ||
| Line 76: | Line 72: | ||
<b>Multiplicative model</b>: $yt=St×Tt×Et$. When the variation in the seasonal pattern, or the variation around the trend-cycle, are proportional to the level of the time series, then a multiplicative model is more appropriate. Note that when using a multiplicative model, we can transform the data to stabilize the variation in the series over time, and then use an additive model. For instance, a log transformation decomposes the multiplicative model from: | <b>Multiplicative model</b>: $yt=St×Tt×Et$. When the variation in the seasonal pattern, or the variation around the trend-cycle, are proportional to the level of the time series, then a multiplicative model is more appropriate. Note that when using a multiplicative model, we can transform the data to stabilize the variation in the series over time, and then use an additive model. For instance, a log transformation decomposes the multiplicative model from: | ||
| − | + | $yt=St×Tt×Et$ <BR> | |
| − | + | to the additive model: <BR> | |
| − | to the additive model: | + | $log(yt)=log(St)+log(Tt)+log(Et).$ |
| − | |||
| − | < | ||
| − | |||
We can examine the Seasonal trends by decomposing the Time Series by <b><i>loess</i></b> (Local Polynomial Regression) Fitting into <b>S</b>easonal, <b>T</b>rend and irregular components using <b>L</b>oess - Local Polynomial Regression Fitting (<b>stl</b> function, in the default “stats” package): | We can examine the Seasonal trends by decomposing the Time Series by <b><i>loess</i></b> (Local Polynomial Regression) Fitting into <b>S</b>easonal, <b>T</b>rend and irregular components using <b>L</b>oess - Local Polynomial Regression Fitting (<b>stl</b> function, in the default “stats” package): | ||
| Line 92: | Line 85: | ||
plot(fit) # data, seasonal, trend, residuals | plot(fit) # data, seasonal, trend, residuals | ||
| − | <center | + | <center>“stl” function parameters</center> |
<center> | <center> | ||
| Line 107: | Line 100: | ||
|t.degree||degree of locally-fitted polynomial in trend extraction. Should be zero or one. | |t.degree||degree of locally-fitted polynomial in trend extraction. Should be zero or one. | ||
|- | |- | ||
| − | |l.window||the span (in lags) of the loess window of the low-pass filter used for each subseries. Defaults to the smallest odd integer greater than or equal | + | |l.window||the span (in lags) of the loess window of the low-pass filter used for each subseries. Defaults to the smallest odd integer greater than or equal to frequency(x) which is recommended since it prevents competition between the trend and seasonal components. If not an odd integer its given value is increased to the next odd one. |
|- | |- | ||
|l.degree||degree of locally-fitted polynomial for the subseries low-pass filter. Must be 0 or 1. | |l.degree||degree of locally-fitted polynomial for the subseries low-pass filter. Must be 0 or 1. | ||
| Line 123: | Line 116: | ||
</center> | </center> | ||
| − | [[Image:SMHS_TimeSeries3.png|400px]] [[Image:SMHS_TimeSeries4.png|400px]] | + | <center>[[Image:SMHS_TimeSeries3.png|400px]] [[Image:SMHS_TimeSeries4.png|400px]]</center> |
<b>monthplot</b>(fit$\$$time.series[,"seasonal"], main="", ylab="Seasonal", lwd=5) | <b>monthplot</b>(fit$\$$time.series[,"seasonal"], main="", ylab="Seasonal", lwd=5) | ||
| Line 132: | Line 125: | ||
#monthplot(fit, choice = <b><u>"remainder"</u></b>, type = "h", cex.axis = 1.2) # histogramatic | #monthplot(fit, choice = <b><u>"remainder"</u></b>, type = "h", cex.axis = 1.2) # histogramatic | ||
| − | [[Image:SMHS_TimeSeries5.png|400px]] | + | <center>[[Image:SMHS_TimeSeries5.png|400px]]</center> |
These are the seasonal plots and seasonal sub-series plots of the seasonal component illustrating the variation in the seasonal component over time (over the years). | These are the seasonal plots and seasonal sub-series plots of the seasonal component illustrating the variation in the seasonal component over time (over the years). | ||
| Line 140: | Line 133: | ||
(See meta-data description and provenance online: [http://weather-warehouse.com/WxWfaqs.html]). | (See meta-data description and provenance online: [http://weather-warehouse.com/WxWfaqs.html]). | ||
| − | + | <center>Mean Temperature, (F), UMich, Ann Arbor (1900-2015)</center> | |
| − | |||
<center> | <center> | ||
{| class="wikitable" style="text-align:center; " border="1" | {| class="wikitable" style="text-align:center; " border="1" | ||
| Line 155: | Line 147: | ||
|2012||22.4||32.8||50.7||49.2||65.2||71.4||78.9||72.2||63.9||51.7||39.6||34.8 | |2012||22.4||32.8||50.7||49.2||65.2||71.4||78.9||72.2||63.9||51.7||39.6||34.8 | ||
|- | |- | ||
| − | |... | + | |...|| || || || || || || || || || || || |
|- | |- | ||
|...||17||15.3||31.4||47.3||57||69||76.6||72||63.4||52.2||35.2||23.7 | |...||17||15.3||31.4||47.3||57||69||76.6||72||63.4||52.2||35.2||23.7 | ||
| Line 185: | Line 177: | ||
<b>Fit the GAMM Model</b> (Generalized Additive Mixed Model) | <b>Fit the GAMM Model</b> (Generalized Additive Mixed Model) | ||
| − | [[Image:SMHS_TimeSeries6.png|400px]] | + | <center>[[Image:SMHS_TimeSeries6.png|400px]]</center> |
<b>Fit a model with trend and seasonal components</b> --- computation may be slow: | <b>Fit a model with trend and seasonal components</b> --- computation may be slow: | ||
| Line 195: | Line 187: | ||
mod <- gamm(as.numeric(temperature) ~ s(as.numeric(Year)) + s(as.numeric(variable)), data = l.sort, method = "REML", correlation=corAR1(form = ~ 1|Year), knots=list(Variable = c(1, 12)), na.action=na.omit, control = ctrl) | mod <- gamm(as.numeric(temperature) ~ s(as.numeric(Year)) + s(as.numeric(variable)), data = l.sort, method = "REML", correlation=corAR1(form = ~ 1|Year), knots=list(Variable = c(1, 12)), na.action=na.omit, control = ctrl) | ||
| − | #<u>Correlation</u>: <b>corStruct</b> object defineing correlation structures in <b>lme</b>. Grouping factors in the formula for this | + | #<u>Correlation</u>: <b>corStruct</b> object defineing correlation structures in <b>lme</b>. Grouping factors in the formula for this<BR> |
| − | + | #object are assumed to be nested within any random effect grouping factors, without the need to make this<BR> | |
| − | #object are assumed to be nested within any random effect grouping factors, without the need to make this | + | #explicit in the formula (somewhat different from the behavior of <b>lme</b>).<BR> |
| − | + | #This is similar to the GEE approach to correlation in the generalized case.<BR> | |
| − | #explicit in the formula (somewhat different from the behavior of <b>lme</b>). | + | #<u>Knots</u>: an optional list of user specified knot values to be used for basis construction --<BR> |
| − | + | #different terms can use different numbers of knots, unless they share a covariate.<BR> | |
| − | #This is similar to the GEE approach to correlation in the generalized case. | + | #If you revise the model like this (below), it will compare nicely with 3 ARMA models (later)<BR> |
| − | + | mod <- gamm(as.numeric(temperature) ~ s(as.numeric(Year), k=116) + s(as.numeric(variable), k=12), | |
| − | #<u>Knots</u>: an optional list of user specified knot values to be used for basis construction -- | + | data = l.sort, correlation = corAR1(form = ~ 1|Year), control = ctrl) |
| − | |||
| − | #different terms can use different numbers of knots, unless they share a covariate. | ||
| − | |||
| − | #If you revise the model like this (below), it will compare nicely with 3 ARMA models (later) | ||
| − | |||
| − | mod <- gamm(as.numeric(temperature) ~ s(as.numeric(Year), k=116) + s(as.numeric(variable), k=12), data = l.sort, correlation = corAR1(form = ~ 1|Year), control = ctrl) | ||
<b>Summary of the fitted model:</b> | <b>Summary of the fitted model:</b> | ||
| Line 220: | Line 206: | ||
t <- cbind(1: 1392) # define the time | t <- cbind(1: 1392) # define the time | ||
| − | [[Image:SMHS_TimeSeries7.png|500px]] | + | <center>[[Image:SMHS_TimeSeries7.png|500px]]</center> |
<b>Plot the trend on the observed data -- with prediction:</b> | <b>Plot the trend on the observed data -- with prediction:</b> | ||
| Line 232: | Line 218: | ||
lines(ptemp2 ~ t, data = l.sort, col = "blue", lwd = 2) | lines(ptemp2 ~ t, data = l.sort, col = "blue", lwd = 2) | ||
| − | [[Image:SMHS_TimeSeries8.png|500px]] | + | <center>[[Image:SMHS_TimeSeries8.png|500px]]</center> |
<b>Plot the seasonal model</b> | <b>Plot the seasonal model</b> | ||
| Line 242: | Line 228: | ||
lines(ptemp, data = l.sort, col = "red", lwd = 0.5) | lines(ptemp, data = l.sort, col = "red", lwd = 0.5) | ||
| − | [[Image:SMHS_TimeSeries9.png|500px]] | + | <center>[[Image:SMHS_TimeSeries9.png|500px]]</center> |
<b>Zoom in first 100 temps (1:100)</b> | <b>Zoom in first 100 temps (1:100)</b> | ||
| Line 248: | Line 234: | ||
plot(l.sort$\$$temperature ~ t, data = l.sort, type = "l", <b>xlim=c(0, 120)</b>, xlab = "year", ylab = expression(Temperature ~ (degree*F))); lines(ptemp, data = l.sort, col = "red", lwd = 0.5) | plot(l.sort$\$$temperature ~ t, data = l.sort, type = "l", <b>xlim=c(0, 120)</b>, xlab = "year", ylab = expression(Temperature ~ (degree*F))); lines(ptemp, data = l.sort, col = "red", lwd = 0.5) | ||
| − | [[Image:SMHS_TimeSeries10.png|500px]] | + | <center>[[Image:SMHS_TimeSeries10.png|500px]]</center> |
To examine how much the estimated trend has changed over the 116 year period, we can use the data contained in <b>pred</b> to compute the difference between the start (Jan 1900) and the end (Dec 2015) of the series in the <i><u>trend</u></i> component only: | To examine how much the estimated trend has changed over the 116 year period, we can use the data contained in <b>pred</b> to compute the difference between the start (Jan 1900) and the end (Dec 2015) of the series in the <i><u>trend</u></i> component only: | ||
| Line 270: | Line 256: | ||
## AR(1) | ## AR(1) | ||
| − | m1 <- gamm(as.numeric(temperature) ~ s(as.numeric(Year), k=116) + s(as.numeric(variable), k=12), data = l.sort, correlation = corARMA(form = ~ 1|Year, <b><u>p = 1</u></b>), control = ctrl) | + | m1 <- gamm(as.numeric(temperature) ~ s(as.numeric(Year), k=116) + s(as.numeric(variable), k=12), |
| − | + | data = l.sort, correlation = corARMA(form = ~ 1|Year, <b><u>p = 1</u></b>), control = ctrl) | |
| + | |||
## AR(2) | ## AR(2) | ||
| − | m2 <- gamm(as.numeric(temperature) ~ s(as.numeric(Year), k=116) + s(as.numeric(variable), k=12), data = l.sort, correlation = corARMA(form = ~ 1|Year, <b><u>p = 2</u></b>), control = ctrl) | + | m2 <- gamm(as.numeric(temperature) ~ s(as.numeric(Year), k=116) + s(as.numeric(variable), k=12), |
| − | + | data = l.sort, correlation = corARMA(form = ~ 1|Year, <b><u>p = 2</u></b>), control = ctrl) | |
| + | |||
## AR(3) | ## AR(3) | ||
| − | m3 <- gamm(as.numeric(temperature) ~ s(as.numeric(Year), k=116) + s(as.numeric(variable), k=12), data = l.sort, correlation = corARMA(form = ~ 1|Year, <b><u>p = 3</u></b>), control = ctrl) | + | m3 <- gamm(as.numeric(temperature) ~ s(as.numeric(Year), k=116) + s(as.numeric(variable), k=12), |
| + | data = l.sort, correlation = corARMA(form = ~ 1|Year, <b><u>p = 3</u></b>), control = ctrl) | ||
| − | Note | + | Note that the correlation argument is specified by <b>corARMA(form = ~ 1|Year, p = x)</b>, which fits an ARMA (auto-regressive moving average) process to the residuals, where <b>p</b> indicates the order for the <b>AR</b> part of the ARMA model, and <b>form = ~ 1|Year</b> specifies that the ARMA is nested within each year. This may expedite the model fitting but may also hide potential residual variation from one year to another. |
| − | Let’s compare the candidate models by using the generalized likelihood ratio test via the <b>anova()</b> method for <b>lme</b> objects | + | Let’s compare the candidate models by using the generalized likelihood ratio test via the <b>anova()</b> method for <b>lme</b> objects; see our previous mixed effects modeling notes <sup>1</sup> , <sup>2</sup>. This model selection is justified as we work with nested models -- going from the AR(3) to the AR(1) by setting some of the AR coefficients to 0. The models also vary in terms of the coefficient estimates for the splines terms which may require fixing some values while choosing the AR structure. |
<b><center>anova(mod$\$$lme, m1$\$$lme, m2$\$$lme, m3$\$$lme)</center></b> | <b><center>anova(mod$\$$lme, m1$\$$lme, m2$\$$lme, m3$\$$lme)</center></b> | ||
| − | |||
| − | |||
| − | |||
<center> | <center> | ||
{| class="wikitable" style="text-align:center; " border="1" | {| class="wikitable" style="text-align:center; " border="1" | ||
|- | |- | ||
| − | |Model||df||AIC||BIC||logLik||Test||L.Ratio||p-value | + | |||Model||df||AIC||BIC||logLik||Test||L.Ratio||p-value |
|- | |- | ||
| − | |mod$\$$lme | + | |mod$\$$lme||1||7||7455.609||7492.228|| -3720.805|| || || |
|- | |- | ||
| − | |m1$\$$lme | + | |m1$\$$lme||2|| 7||7455.609||7492.228|| -3720.805|| || || |
|- | |- | ||
| − | |m2$\$$lme | + | |m2$\$$lme||3|| 8||7453.982||7495.832|| -3718.991||2 vs 3||3.627409||0.0568 |
|- | |- | ||
| − | |m3$\$$lme | + | |m3$\$$lme||4|| 9||7455.966||7503.048|| -3718.983|| 3 vs 4||0.015687||0.9003 |
|} | |} | ||
</center> | </center> | ||
| − | + | <b>Interpretation </b> | |
The AR(1) model (m1) does not provide a substantial increase in fit over the naive model (mod), and the AR(2) model (m2) only provides a marginal increase in the AR(1) model fit (m1). There is no improvement in moving from m2 to AR(3) model (m3). | The AR(1) model (m1) does not provide a substantial increase in fit over the naive model (mod), and the AR(2) model (m2) only provides a marginal increase in the AR(1) model fit (m1). There is no improvement in moving from m2 to AR(3) model (m3). | ||
| Line 309: | Line 295: | ||
plot(m2$\$$gam, scale = 0) # plot(mod2$\$$gam, scale = 0) # “scale=0” ensures optimal y-axis cropping of plot | plot(m2$\$$gam, scale = 0) # plot(mod2$\$$gam, scale = 0) # “scale=0” ensures optimal y-axis cropping of plot | ||
| − | [[Image:SMHS_TimeSeries11.png|500px]] | + | <center>[[Image:SMHS_TimeSeries11.png|500px]]</center> |
<b>Investigation of residual patterns</b> | <b>Investigation of residual patterns</b> | ||
| Line 318: | Line 304: | ||
# pACF controls for the values of the time series at all shorter lags, which contrasts the ACF which does not control for other lags. | # pACF controls for the values of the time series at all shorter lags, which contrasts the ACF which does not control for other lags. | ||
| − | [[Image:SMHS_TimeSeries12.png|500px]] | + | <center>[[Image:SMHS_TimeSeries12.png|500px]]</center> |
This illustrates that there is some (month=1) Auto-correlation (ACF) and partial auto correlation in the residuals. | This illustrates that there is some (month=1) Auto-correlation (ACF) and partial auto correlation in the residuals. | ||
| Line 328: | Line 314: | ||
layout(1) | layout(1) | ||
| − | [[Image:SMHS_TimeSeries13.png|500px]] | + | <center>[[Image:SMHS_TimeSeries13.png|500px]]</center> |
No residual auto-correlation remains in <b>m2</b>. The resulting fitted Generalized Additive Mixed Model (GAMM) object contains information about the trend and the contributions to the fitted values. The package '''mgcv'''<sup>3</sup> can spit the information using <b>predict()</b> for each of the 4 models. | No residual auto-correlation remains in <b>m2</b>. The resulting fitted Generalized Additive Mixed Model (GAMM) object contains information about the trend and the contributions to the fitted values. The package '''mgcv'''<sup>3</sup> can spit the information using <b>predict()</b> for each of the 4 models. | ||
| Line 347: | Line 333: | ||
lines(x=df_time, y=pred_season2, data = l.sort, col = "blue", lwd = 2) | lines(x=df_time, y=pred_season2, data = l.sort, col = "blue", lwd = 2) | ||
| − | [[Image:SMHS_TimeSeries14.png|500px]] | + | <center>[[Image:SMHS_TimeSeries14.png|500px]]</center> |
===Moving average smoothing=== | ===Moving average smoothing=== | ||
| − | + | A moving average of order $m=2k+1$ can be expressed as: | |
| − | |||
| − | |||
$T_{t}=\frac{1}{2k+1}\sum_{j=-k}^{k}Y_{t+j}$ . | $T_{t}=\frac{1}{2k+1}\sum_{j=-k}^{k}Y_{t+j}$ . | ||
| − | |||
| − | + | The ''m''-MA represents an order m moving average, $T_t$, or the estimate of the trend-cycle at time ''t'', obtained by averaging values of the time series within ''k'' periods (left and right) of ''t''. This averaging process denoises the data (eliminates randomness in the data) and produces a smoother trend-cycle component. | |
| − | + | The 5-MA contains the values of $T_t$ with ''k''=2. To see what the trend-cycle estimate looks like, we plot it along with the original data | |
# print the moving average results (k=3 ↔ m=7) | # print the moving average results (k=3 ↔ m=7) | ||
| Line 373: | Line 356: | ||
lwd=c(2.5,2.5), col=c("black", "red", "blue")) # gives the legend lines the correct color and width | lwd=c(2.5,2.5), col=c("black", "red", "blue")) # gives the legend lines the correct color and width | ||
| − | [[Image:SMHS_TimeSeries15.png|500px]] | + | <center>[[Image:SMHS_TimeSeries15.png|500px]]</center> |
| − | + | The blue trend (''k''=36) (3 yrs) is smoother than the original (raw) data (black) and the 1-yr average (''k''=12). It captures the main movement of the time series without all the minor fluctuations. We can’t estimate $T_t$ where ''t'' is close to the ends as there is not enough data there to compute the averages. The red trend (''k''=12) is smoother than the original (raw) data (black) but more jagged than the 3-yr average. The order of the moving average (''m'') determines the smoothness of the trend-cycle estimate. A larger order implies a smoother curve. | |
===Simulation of a time-series analysis and prediction=== | ===Simulation of a time-series analysis and prediction=== | ||
| Line 399: | Line 382: | ||
lines(sim_ts2, col="blue", lwd=3) | lines(sim_ts2, col="blue", lwd=3) | ||
| − | [[Image:SMHS_TimeSeries16.png|500px]] | + | <center>[[Image:SMHS_TimeSeries16.png|500px]]</center> |
| − | ===Seasonal Decomposition=== | + | ====Seasonal Decomposition==== |
| − | |||
| − | |||
| + | *The additive and seasonal trends, and irregular components, of time-series may be decomposed using the stl() function. Series with multiplicative effects can by transformed into series with additive effects through a log transformation (i.e., '''ln_sim_ts <- log(sim_ts)). | ||
# Seasonal decomposition | # Seasonal decomposition | ||
fit_stl <- stl(sim_ts, s.window="period") '''# Seasonal Decomposition of Time Series by Loess''' | fit_stl <- stl(sim_ts, s.window="period") '''# Seasonal Decomposition of Time Series by Loess''' | ||
| Line 413: | Line 395: | ||
| − | [[Image:SMHS_TimeSeries17.png|500px]] | + | <center>[[Image:SMHS_TimeSeries17.png|500px]]</center> |
# additional plots | # additional plots | ||
| Line 421: | Line 403: | ||
seasonplot(sim_ts) | seasonplot(sim_ts) | ||
| − | ===Exponential Models=== | + | ====Exponential Models==== |
*The '''HoltWinters()''' function ('''stats''' package), and the '''ets()''' function ('''forecast''' package) can fit exponential models. | *The '''HoltWinters()''' function ('''stats''' package), and the '''ets()''' function ('''forecast''' package) can fit exponential models. | ||
| Line 440: | Line 422: | ||
# clear plot: | # clear plot: | ||
# dev.off() | # dev.off() | ||
| − | + | <center>[[Image:SMHS_TimeSeries18.png|500px]]</center> | |
| − | [[Image:SMHS_TimeSeries18.png|500px]] | ||
===Auto-regressive Integrated Moving Average (ARIMA) Models<sup>4</sup> === | ===Auto-regressive Integrated Moving Average (ARIMA) Models<sup>4</sup> === | ||
| − | + | There are 2 types of ARIMA time-series models: <BR> | |
| − | X_t=\mu+ \sum_{i=1}^{p}φ_iX_{t-i} + \sum_{j=1}^{q}θ_jε_{t-j} | + | $ X_t= \mu+ \underbrace{\sum_{i=1}^{p}{φ_iX_{t-i}}}_\text{auto-regressive (p) part} + |
| − | \ | + | \underbrace{\sum_{j=1}^{q}{θ_jε_{t-j}}}_\text{moving-average (q) part} + |
| − | + | \underbrace{ ε_t }_\text{error term}.$ | |
| − | |||
| − | |||
| − | + | ====Non-seasonal ARIMA models==== | |
| − | + | The Non-seasonal ARIMA models are denoted by ARIMA(p, d, q), where parameters p, d, and q are positive integers, | |
| − | + | * p = order of the auto-regressive model, | |
| − | + | * d = degree of differencing, when ''d''=2, the '''''d<sup>th</sup>'' difference''' is $(X_t-X_{t-1})-(X_{t-1}-X_{t-2})= X_t-2X_{t-1}+X_{t-2}$. That is, the second difference of ''X'' (d=2) is not the difference between the current period and the value 2 periods ago. It is the first-difference-of-the-first difference, the discrete analog of a second derivative, representing the local acceleration of the series rather than its local trend (first derivative). | |
| − | *p = order of the auto-regressive model, | + | * q = order of the moving-average model. |
| − | *d = degree of differencing, when ''d''=2, the '''''d<sup>th</sup>'' difference''' is | ||
| − | |||
| − | |||
| − | |||
| − | That | ||
| − | *q = order of the moving-average model. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | ====Seasonal ARIMA models==== | ||
| + | The Seasonal AMIMA models are denoted by ''ARIMA(p, d, q)(P, D, Q)<sub>m</sub>,'' | ||
| + | * m = number of periods in each season, | ||
| + | * uppercase P, D, Q represent the auto-regressive, differencing, and moving average terms for the seasonal part of the ARIMA model, and the lower case (p,d,q) are as with non-seasonal ARIMA. | ||
If 2 of the 3 terms are trivial, the model is abbreviated using the non-zero parameter, skipping the "AR", "I" or "MA" from the acronym. For example, | If 2 of the 3 terms are trivial, the model is abbreviated using the non-zero parameter, skipping the "AR", "I" or "MA" from the acronym. For example, | ||
| − | *ARIMA(1,0,0) = AR(1), a stationary and auto-correlated series can be predicted as a multiple of its own previous value, plus a constant. $X_t=μ + φ_1 × X_{t-1}+ \epsilon_t.$ Note that $ε_t=X_t-\hat{X}_t.$ | + | *ARIMA(1,0,0) = AR(1), a stationary and auto-correlated series can be predicted as a multiple of its own previous value, plus a constant. $X_t=μ + φ_1 × X_{t-1}+ \epsilon_t.$ Note that $ε_t=X_t-\hat{X}_t.$ |
*An ARIMA(0,1,0) = I(1) model, not stationary series, a limiting case of an AR(1) model, the auto-regressive coefficient is equal to 1, i.e., a series with infinitely slow mean reversion, $X_t=μ+X_{t-1}+ε_t,$ a 1-step random walk. | *An ARIMA(0,1,0) = I(1) model, not stationary series, a limiting case of an AR(1) model, the auto-regressive coefficient is equal to 1, i.e., a series with infinitely slow mean reversion, $X_t=μ+X_{t-1}+ε_t,$ a 1-step random walk. | ||
| − | For more complex models: | + | <B>For more complex models:</B> |
| − | |||
*An ARIMA(1,1,0), differenced first-order auto-regressive model. $X_t=μ+X_{t-1}+α×(X_{t-1}-X_{t-2})+ε_t.$ | *An ARIMA(1,1,0), differenced first-order auto-regressive model. $X_t=μ+X_{t-1}+α×(X_{t-1}-X_{t-2})+ε_t.$ | ||
| Line 483: | Line 454: | ||
*ARIMA(1,1,2), $X_t=μ+X_{t-1}+(X_{t-1}+X_{t-2})+α×ε{t}+β×ε_{t-1}$ | *ARIMA(1,1,2), $X_t=μ+X_{t-1}+(X_{t-1}+X_{t-2})+α×ε{t}+β×ε_{t-1}$ | ||
| − | |||
The '''arima'''() function ('''stats''' package) can be used to fit an <b><u>auto-regressive integrated moving averages</u></b> model. Other useful functions include: | The '''arima'''() function ('''stats''' package) can be used to fit an <b><u>auto-regressive integrated moving averages</u></b> model. Other useful functions include: | ||
| − | + | * lag(sim_ts, k) lagged version of time series, shifted back k observations | |
| − | *lag(sim_ts, k) lagged version of time series, shifted back k observations | + | * diff(sim_ts, differences=d) difference the time series d times |
| − | + | * ndiffs(sim_ts) Number of differences required to achieve stationarity (from the forecast package) | |
| − | *diff(sim_ts, differences=d) difference the time series d times | + | * acf(sim_ts) auto-correlation function |
| − | + | * pacf(sim_ts) partial auto-correlation function | |
| − | *ndiffs(sim_ts) Number of differences required to achieve stationarity (from the forecast package) | + | * adf.test(sim_ts) Augmented Dickey-Fuller test. Rejecting the null hypothesis suggests that a time series is stationary (from the tseries package)</li> |
| − | + | * Box.test(x, type="Ljung-Box") Portmanteau test that observations in vector or time series x are independent. | |
| − | *acf(sim_ts) auto-correlation function | ||
| − | |||
| − | *pacf(sim_ts) partial auto-correlation function | ||
| − | |||
| − | *adf.test(sim_ts) Augmented Dickey-Fuller test. Rejecting the null hypothesis suggests that a time series is stationary (from the tseries package) | ||
| − | |||
| − | *Box.test(x, type="Ljung-Box") Portmanteau test that observations in vector or time series x are independent | ||
| − | |||
The '''forecast''' package has alternative versions of '''acf()''' and '''pacf()''' called '''Acf()''' and '''Pacf()''' respectively. | The '''forecast''' package has alternative versions of '''acf()''' and '''pacf()''' called '''Acf()''' and '''Pacf()''' respectively. | ||
| − | |||
# fit an '''ARIMA(P, D, Q) model''' of order: | # fit an '''ARIMA(P, D, Q) model''' of order: | ||
| + | * P, represents the AR order< | ||
| + | * D, represents the degree of differencing | ||
| + | * Q, represents the MA order. | ||
| − | + | fit_arima1 <- arima(sim_ts, order=c(3, 1, 2)) | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | fit_arima1 <- arima(sim_ts, order=c(3, 1, 2)) | ||
| − | |||
# predictive accuracy | # predictive accuracy | ||
library(forecast) | library(forecast) | ||
| Line 525: | Line 480: | ||
plot(forecast(fit_arima1, 20)) | plot(forecast(fit_arima1, 20)) | ||
| − | [[Image:SMHS_TimeSeries19.png|600px]] | + | <center>[[Image:SMHS_TimeSeries19.png|600px]]</center> |
===Automated Forecasting=== | ===Automated Forecasting=== | ||
| − | + | The '''forecast''' package provides functions for the automatic selection of exponential and ARIMA models. The '''ets()''' (exponential TS) function supports both additive and multiplicative models. The '''auto.arima()''' function accounts for seasonal and nonseasonal ARIMA models according to criteria maximizing a cost function. | |
| − | + | # library(forecast) | |
| − | + | ||
| − | # library(forecast) | + | # Automated forecasting using an exponential model |
| − | + | fit_ets <- ets(sim_ts) | |
| − | # Automated forecasting using an exponential model | ||
| − | |||
# Automated forecasting using an ARIMA model | # Automated forecasting using an ARIMA model | ||
| Line 544: | Line 497: | ||
fit_ets$\$$aic; fit_arima2$\$$aic | fit_ets$\$$aic; fit_arima2$\$$aic | ||
accuracy(fit_ets); accuracy(fit_arima2); | accuracy(fit_ets); accuracy(fit_arima2); | ||
| − | |||
'''Akaike’s Information Criterion (AIC)''' = ''-2Log(Likelihood)+2p,'' where ''p'' is he number of estimated parameters. | '''Akaike’s Information Criterion (AIC)''' = ''-2Log(Likelihood)+2p,'' where ''p'' is he number of estimated parameters. | ||
| − | |||
| − | |||
| − | |||
summary(fit_ets); summary(fit_arima2) | summary(fit_ets); summary(fit_arima2) | ||
ACF plot of the residuals from the ARIMA(3,1,2) model shows all correlations within the threshold limits indicating that the residuals are behaving like white noise. A portmanteau test returns a large p-value, also suggesting the residuals are white noise. | ACF plot of the residuals from the ARIMA(3,1,2) model shows all correlations within the threshold limits indicating that the residuals are behaving like white noise. A portmanteau test returns a large p-value, also suggesting the residuals are white noise. | ||
| − | + | # acf computes (and by default plots) estimates of the autocovariance or autocorrelation function | |
| − | # acf computes (and by default plots) estimates of the autocovariance or autocorrelation function | ||
acf(residuals(fit_ets)) | acf(residuals(fit_ets)) | ||
| − | # Box–Pierce or Ljung–Box test statistic for examining the null hypothesis of independence in a given time series. | + | # Box–Pierce or Ljung–Box test statistic for examining the null hypothesis of independence in a given time series. |
| − | + | # These are sometimes known as ‘portmanteau’ tests. | |
| − | # These are sometimes known as ‘portmanteau’ tests. | ||
| − | |||
Box.test(residuals(fit_ets), lag=24, fitdf=4, type="Ljung") | Box.test(residuals(fit_ets), lag=24, fitdf=4, type="Ljung") | ||
| − | + | # plot forecast | |
| − | # plot forecast | ||
plot(forecast(fit_arima2)) | plot(forecast(fit_arima2)) | ||
| − | + | # more on ARIMA https://www.otexts.org/fpp/8/7 | |
| − | # more on ARIMA https://www.otexts.org/fpp/8/7 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <sup>3</sup> https://cran.r-project.org/web/packages/mgcv/mgcv.pdf | + | ===Footnotes=== |
| + | * <sup>1</sup> https://umich.instructure.com/files/689861/download?download_frd=1 | ||
| + | * <sup>2</sup> https://umich.instructure.com/courses/38100/files | ||
| + | * <sup>3</sup> https://cran.r-project.org/web/packages/mgcv/mgcv.pdf | ||
| + | * <sup>4</sup> http://arxiv.org/ftp/arxiv/papers/1302/1302.6613.pdf | ||
==See also== | ==See also== | ||
| Line 582: | Line 524: | ||
<hr> | <hr> | ||
* SOCR Home page: http://www.socr.ucla.edu | * SOCR Home page: http://www.socr.ucla.edu | ||
| − | {{translate|pageName=http://wiki. | + | "{{translate|pageName=http://wiki.socr.umich.edu/index.php?title=SMHS_TimeSeriesAnalysis}} |
Latest revision as of 14:36, 3 March 2020
Contents
- 1 Scientific Methods for Health Sciences - Time Series Analysis
- 2 See also
Scientific Methods for Health Sciences - Time Series Analysis
Questions
- Why are trends, patterns or predictions from models/data important?
- How to detect, model and utilize trends in longitudinal data?
Time series analysis represents a class of statistical methods applicable for series data aiming to extract meaningful information, trend and characterization of the process using observed longitudinal data. These trends may be used for time series forecasting and for prediction of future values based on retrospective observations. Note that classical linear modeling (e.g., regression analysis) may also be employed for prediction & testing of associations using the values of one or more independent variables and their effect on the value of another variable. However, time series analysis allows dependencies (e.g., seasonal effects to be accounted for).
Time-series representation
There are 3 (distinct and complementary) types of time series patterns that most time-series analyses are trying to identify, model and analyze. These include:
- Trend: A trend is a long-term increase or decrease in the data that may be linear or non-linear, but is generally continuous (mostly monotonic). The trend may be referred to as direction.
- Seasonal: A seasonal pattern is influence in the data, like seasonal factors (e.g., the quarter of the year, the month, or day of the week), which is always of a fixed known period.
- Cyclic: A cyclic pattern of fluctuations corresponds to rises and falls that are not of fixed period.
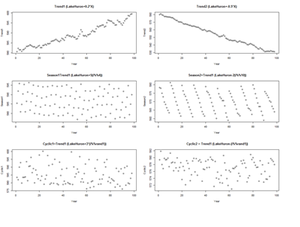
For example, the following code shows several time series with different types of time series patterns.
par(mfrow=c(3,2))
n <- 98
X <- cbind(1:n) # time points (annually)
Trend1 <- LakeHuron+0.2*X # series 1
Trend2 <- LakeHuron-0.5*X # series 2
Season1 <- X; Season2 <- X; # series 1 & 2
for(i in 1:n) {
Season1[i] <- LakeHuron[i] + 5*(i%%4)
Season2[i] <- LakeHuron[i] -2*(i%%10)
}
Cyclic1 <- X; Cyclic2 <- X; # series 1 & 2
for(i in 1:n) {
rand1 <- as.integer(runif(1, 1, 10))
Cyclic1[i] <- LakeHuron[i] + 3*(i%%rand1)
Cyclic2[i] <- LakeHuron[i] - 1*(i%%rand1)
}
plot(X, Trend1, xlab="Year",ylab=" Trend1", main="Trend1 (LakeHuron+0.2*X)")
plot(X, Trend2, xlab="Year",ylab=" Trend2" , main="Trend2 (LakeHuron-0.5*X)")
plot(X, Season1, xlab="Year",ylab=" Season1", main=" Season1=Trend1 (LakeHuron+5(i%%4))")
plot(X, Season2, xlab="Year",ylab=" Season2", main=" Season2=Trend1 (LakeHuron-2(i%%10))")
plot(X, Cyclic1, xlab="Year",ylab=" Cyclic1", main=" Cyclic1=Trend1 (LakeHuron+3*(i%%rand1))")
plot(X, Cyclic2, xlab="Year",ylab=" Cyclic2", main=" Cyclic2 = Trend1 (LakeHuron-(i%%rand1))")
Note: If you get this run-time graphics error:
“Error in plot.new() : figure margins too large”
You need to make sure your graphics window is large enough or print to PDF:
pdf("myplot.pdf"); plot(x); dev.off()
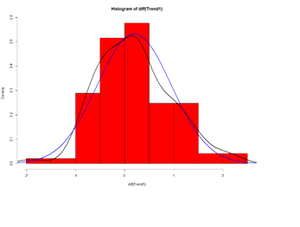
Let’s look at the delta (Δ) changes - Lagged Differences, using diff, which returns suitably lagged and iterated differences.
## Default lag = 1 par(mfrow=c(1,1)) hist(diff(Trend1), prob=T, col="red") # Plot histogram lines(density(diff(Trend1)),lwd=2) # plot density estimate x<-seq(-4,4,length=100); y<-dnorm(x, mean(diff(Trend1)), sd(diff(Trend1))) lines(x,y,lwd=2,col="blue") # plot MLE Normal Fit
Time series decomposition
Denote the time series $yt$ including the three components: a seasonal effect, a trend-cycle effect (containing both trend and cycle), and a remainder component (containing the residual variability in the time series).
Additive model: $yt=St+Tt+Et,$ where $yt$ is the data at period $t, St$ is the seasonal component at period $t, Tt$ is the trend-cycle component at period $t$ and $Et$ is the remainder (error) component at period $t$. This additive model is appropriate if the magnitude of the seasonal fluctuations or the variation around the trend-cycle does not vary with the level of the time series.
Multiplicative model: $yt=St×Tt×Et$. When the variation in the seasonal pattern, or the variation around the trend-cycle, are proportional to the level of the time series, then a multiplicative model is more appropriate. Note that when using a multiplicative model, we can transform the data to stabilize the variation in the series over time, and then use an additive model. For instance, a log transformation decomposes the multiplicative model from:
$yt=St×Tt×Et$
to the additive model:
$log(yt)=log(St)+log(Tt)+log(Et).$
We can examine the Seasonal trends by decomposing the Time Series by loess (Local Polynomial Regression) Fitting into Seasonal, Trend and irregular components using Loess - Local Polynomial Regression Fitting (stl function, in the default “stats” package):
# using Monthly Males Deaths from Lung Diseases in UK from bronchitis, emphysema and asthma, 1974–1979
mdeaths # is.ts(mdeaths)
fit <- stl(mdeaths, s.window=5)
plot(mdeaths, col="gray", main=" Lung Diseases in UK ", ylab=" Lung Diseases Deaths", xlab="")
lines(fit\$\$$time.series[,2],col="red",ylab="Trend")
plot(fit) # data, seasonal, trend, residuals
<center>“stl” function parameters</center>
<center>
{| class="wikitable" style="text-align:center; " border="1"
|-
|x||Univariate time series to be decomposed. This should be an object of class "ts" with a frequency greater than one.
|-
|s.window||either the character string "periodic" or the span (in lags) of the loess window for seasonal extraction, which should be odd and at least 7, according to Cleveland et al. This has no default.
|-
|s.degree||degree of locally-fitted polynomial in seasonal extraction. Should be zero or one.
|-
|t.window||the span (in lags) of the loess window for trend extraction, which should be odd. If NULL, the default, nextodd(ceiling((1.5*period) / (1-(1.5/s.window)))), is taken.
|-
|t.degree||degree of locally-fitted polynomial in trend extraction. Should be zero or one.
|-
|l.window||the span (in lags) of the loess window of the low-pass filter used for each subseries. Defaults to the smallest odd integer greater than or equal to frequency(x) which is recommended since it prevents competition between the trend and seasonal components. If not an odd integer its given value is increased to the next odd one.
|-
|l.degree||degree of locally-fitted polynomial for the subseries low-pass filter. Must be 0 or 1.
|-
|s.jump, t.jump, l.jump||integers at least one to increase speed of the respective smoother. Linear interpolation happens between every *.jump<sup>th</sup> value.
|-
|robust||logical indicating if robust fitting be used in the loess procedure.
|-
|inner||integer; the number of ‘inner’ (backfitting) iterations; usually very few (2) iterations suffice.
|-
|outer||integer; the number of ‘outer’ robustness iterations.
|-
|na.action||action on missing values.
|}
</center>
<center>[[Image:SMHS_TimeSeries3.png|400px]] [[Image:SMHS_TimeSeries4.png|400px]]</center>
<b>monthplot</b>(fit$\$$time.series[,"seasonal"], main="", ylab="Seasonal", lwd=5)
#As the “fit <- stl(mdeaths, s.window=5)” object has 3 time-series components (seasonal; trend; remainder)
#we can alternatively plot them separately:
#monthplot(fit, choice = "seasonal", cex.axis = 0.8)
#monthplot(fit, choice = "trend", cex.axis = 0.8)
#monthplot(fit, choice = "remainder", type = "h", cex.axis = 1.2) # histogramatic
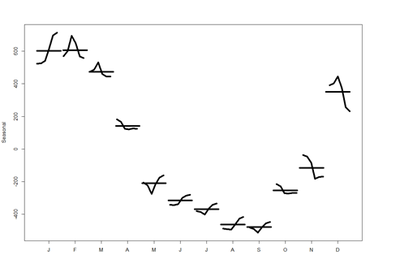
These are the seasonal plots and seasonal sub-series plots of the seasonal component illustrating the variation in the seasonal component over time (over the years).
Using historical weather (average daily temperature at the University of Michigan, Ann Arbor): [1] (See meta-data description and provenance online: [2]).
| Year | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2015 | 26.3 | 14.4 | 34.9 | 49 | 64.2 | 68 | 71.2 | 70.2 | 68.7 | 53.9 | NR | NR |
| 2014 | 24.4 | 19.4 | 29 | 48.9 | 60.7 | 69.7 | 68.8 | 70.8 | 63.2 | 52.1 | 35.4 | 33.3 |
| 2013 | 22.7 | 26.1 | 33.3 | 46 | 63.1 | 68.5 | 72.9 | 70.2 | 64.6 | 53.2 | 37.6 | 26.7 |
| 2012 | 22.4 | 32.8 | 50.7 | 49.2 | 65.2 | 71.4 | 78.9 | 72.2 | 63.9 | 51.7 | 39.6 | 34.8 |
| ... | ||||||||||||
| ... | 17 | 15.3 | 31.4 | 47.3 | 57 | 69 | 76.6 | 72 | 63.4 | 52.2 | 35.2 | 23.7 |
| 1900 | 21.4 | 19.2 | 24.7 | 47.8 | 60.2 | 66.3 | 72 | 75.4 | 67.2 | 59 | 37.6 | 29.2 |
# data: 07_UMich_AnnArbor_MI_TempPrecipitation_HistData_1900_2015.csv
# more complete data is available here: 07_UMich_AnnArbor_MI_TempPrecipitation_HistData_1900_2015.xls umich_data <- read.csv("https://umich.instructure.com/files/702739/download?download_frd=1", header=TRUE)
head(umich_data)
# https://cran.r-project.org/web/packages/mgcv/mgcv.pdf
# install.packages("mgcv"); require(mgcv)
# install.packages("gamair"); require(gamair)
par(mfrow=c(1,1))
The data are in wide format – convert to long format for plotting
# library("reshape2")
long_data <- melt(umich_data, id.vars = c("Year"), value.name = "temperature")
l.sort <- long_data[order(long_data$\$$Year),]
head(l.sort); tail(l.sort)
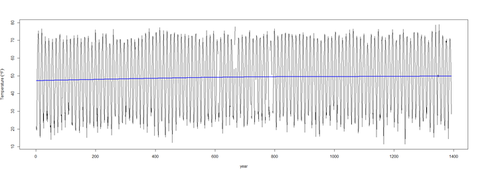
plot(l.sort$\$$temperature, data = l.sort, type = "l")
Fit the GAMM Model (Generalized Additive Mixed Model)
Fit a model with trend and seasonal components --- computation may be slow:
# define the parameters controlling the process of model-fitting/parameter-estimation ctrl <- list(niterEM = 0, msVerbose = TRUE, optimMethod="L-BFGS-B") # First try this model mod <- gamm(as.numeric(temperature) ~ s(as.numeric(Year)) + s(as.numeric(variable)), data = l.sort, method = "REML", correlation=corAR1(form = ~ 1|Year), knots=list(Variable = c(1, 12)), na.action=na.omit, control = ctrl)
#Correlation: corStruct object defineing correlation structures in lme. Grouping factors in the formula for this
#object are assumed to be nested within any random effect grouping factors, without the need to make this
#explicit in the formula (somewhat different from the behavior of lme).
#This is similar to the GEE approach to correlation in the generalized case.
#Knots: an optional list of user specified knot values to be used for basis construction --
#different terms can use different numbers of knots, unless they share a covariate.
#If you revise the model like this (below), it will compare nicely with 3 ARMA models (later)
mod <- gamm(as.numeric(temperature) ~ s(as.numeric(Year), k=116) + s(as.numeric(variable), k=12), data = l.sort, correlation = corAR1(form = ~ 1|Year), control = ctrl)
Summary of the fitted model:
summary(mod$\$$gam) <b>Visualize the model trend (year) and seasonal terms (months)</b> plot(mod$\$$gam, pages = 1) t <- cbind(1: 1392) # define the time
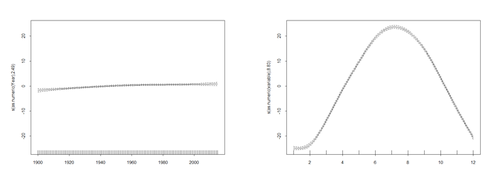
Plot the trend on the observed data -- with prediction:
pred2 <- predict(mod$\$$gam, newdata = l.sort, type = "terms") ptemp2 <- attr(pred2, "constant") + <u>pred2[,1]</u> <b># pred2[,1] = trend; pred2[,2] = seasonal effects</b> <b># mod$\$$gam is a GAM object containing information to use predict, summary and print methods, but not to use e.g. the anova method function to compare models plot(temperature ~ t, data = l.sort, type = "l", xlab = "year", ylab = expression(Temperature ~ (degree*F))) lines(ptemp2 ~ t, data = l.sort, col = "blue", lwd = 2)
Plot the seasonal model
pred <- predict(mod$\$$gam, newdata = l.sort, type = "terms") ptemp <- attr(pred, "constant") + <u>pred[,2]</u> plot(l.sort$\$$temperature ~ t, data = l.sort, type = "l", xlab = "year", ylab = expression(Temperature ~ (degree*F))) lines(ptemp, data = l.sort, col = "red", lwd = 0.5)
Zoom in first 100 temps (1:100)
plot(l.sort$\$$temperature ~ t, data = l.sort, type = "l", <b>xlim=c(0, 120)</b>, xlab = "year", ylab = expression(Temperature ~ (degree*F))); lines(ptemp, data = l.sort, col = "red", lwd = 0.5)
<center>[[Image:SMHS_TimeSeries10.png|500px]]</center>
To examine how much the estimated trend has changed over the 116 year period, we can use the data contained in <b>pred</b> to compute the difference between the start (Jan 1900) and the end (Dec 2015) of the series in the <i><u>trend</u></i> component only:
<b>tail(pred[,1], 1) - head(pred[,1], 1)</b> # subtract the predicted temp [,1] in 1900 (head) from the temp in 2015 (tail)
# names(attributes(pred)); str(pred) # to see the components of the GAM prediction model object (pred)
<b>Assess autocorrelation in residuals</b>
# head(umich_data); tail(umich_data)
acf(resid(mod$\$$lme), lag.max = 36, main = "ACF")
# acf = Auto-correlation and Cross-Covariance Function computes and plots the estimates of the autocovariance or autocorrelation function.
# pacf is the function used for the partial autocorrelations.
# ccf computes the cross-correlation or cross-covariance of two univariate series.
pacf(resid(mod$\$$lme), lag.max = 36, main = "pACF")
Looking at the residuals of this model, using the (partial) autocorrelation function, we see that there may be some residual autocorrelation in the data that the trend term didn’t account for. The shapes of the ACF and the pACF suggest an <b>AR(p)</b> model might be appropriate.
<b>Fit and compare 4 alternative autoregressive models (original mod, AR1, AR2 and AR3)</b>
## AR(1)
m1 <- gamm(as.numeric(temperature) ~ s(as.numeric(Year), k=116) + s(as.numeric(variable), k=12),
data = l.sort, correlation = corARMA(form = ~ 1|Year, <b><u>p = 1</u></b>), control = ctrl)
## AR(2)
m2 <- gamm(as.numeric(temperature) ~ s(as.numeric(Year), k=116) + s(as.numeric(variable), k=12),
data = l.sort, correlation = corARMA(form = ~ 1|Year, <b><u>p = 2</u></b>), control = ctrl)
## AR(3)
m3 <- gamm(as.numeric(temperature) ~ s(as.numeric(Year), k=116) + s(as.numeric(variable), k=12),
data = l.sort, correlation = corARMA(form = ~ 1|Year, <b><u>p = 3</u></b>), control = ctrl)
Note that the correlation argument is specified by <b>corARMA(form = ~ 1|Year, p = x)</b>, which fits an ARMA (auto-regressive moving average) process to the residuals, where <b>p</b> indicates the order for the <b>AR</b> part of the ARMA model, and <b>form = ~ 1|Year</b> specifies that the ARMA is nested within each year. This may expedite the model fitting but may also hide potential residual variation from one year to another.
Let’s compare the candidate models by using the generalized likelihood ratio test via the <b>anova()</b> method for <b>lme</b> objects; see our previous mixed effects modeling notes <sup>1</sup> , <sup>2</sup>. This model selection is justified as we work with nested models -- going from the AR(3) to the AR(1) by setting some of the AR coefficients to 0. The models also vary in terms of the coefficient estimates for the splines terms which may require fixing some values while choosing the AR structure.
<b><center>anova(mod$\$$lme, m1$\$$lme, m2$\$$lme, m3$\$$lme)</center></b>
<center>
{| class="wikitable" style="text-align:center; " border="1"
|-
|||Model||df||AIC||BIC||logLik||Test||L.Ratio||p-value
|-
|mod$\$$lme||1||7||7455.609||7492.228|| -3720.805|| || ||
|- |m1$\$$lme||2|| 7||7455.609||7492.228|| -3720.805|| || || |- |m2$\$$lme||3|| 8||7453.982||7495.832|| -3718.991||2 vs 3||3.627409||0.0568 |- |m3$\$$lme||4|| 9||7455.966||7503.048|| -3718.983|| 3 vs 4||0.015687||0.9003 |} </center> <b>Interpretation </b> The AR(1) model (m1) does not provide a substantial increase in fit over the naive model (mod), and the AR(2) model (m2) only provides a marginal increase in the AR(1) model fit (m1). There is no improvement in moving from m2 to AR(3) model (m3). Let’s plot the AR(2) model (m2) to inspect how over-fitted the naive model with uncorrelated errors was in terms of the trend term, which shows similar smoothness compared to the initial (mod) model. plot(m2$\$$gam, scale = 0) # plot(mod2$\$$gam, scale = 0) # “scale=0” ensures optimal y-axis cropping of plot <center>[[Image:SMHS_TimeSeries11.png|500px]]</center> <b>Investigation of residual patterns</b> layout(matrix(1:2, ncol = 2)) # original (mod) model acf(resid(mod$\$$lme), lag.max = 36, main = "ACF"); pacf(resid(mod$\$$lme), lag.max = 36, main = "pACF") # pACF controls for the values of the time series at all shorter lags, which contrasts the ACF which does not control for other lags. <center>[[Image:SMHS_TimeSeries12.png|500px]]</center> This illustrates that there is some (month=1) Auto-correlation (ACF) and partial auto correlation in the residuals. # ARM(2) model (m2) layout(matrix(1:2, ncol = 2)) res <- resid(m2$\$$lme, type = "normalized");
acf(res, lag.max = 36, main = "ACF - AR(2) errors"); pacf(res, lag.max = 36, main = "pACF- AR(2) errors") layout(1)
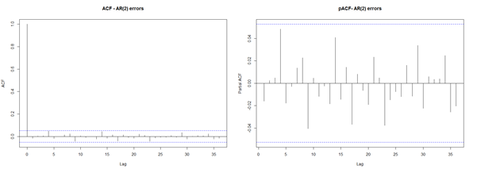
No residual auto-correlation remains in m2. The resulting fitted Generalized Additive Mixed Model (GAMM) object contains information about the trend and the contributions to the fitted values. The package mgcv3 can spit the information using predict() for each of the 4 models.
# require(mgcv); require(gamair)
# m2 <- gamm(as.numeric(temperature) ~ s(as.numeric(Year), k=116) + s(as.numeric(variable), k=12), data = l.sort, correlation = corARMA(form = ~ 1|Year, p = 2), control = ctrl)
pred2 <- predict(m2$\$$gam, newdata = l.sort, type = "terms")
pred_trend2 <- attr(pred2, "constant") + <u>pred2[,1]</u> <b># trend</b>
pred_season2 <- attr(pred2, "constant") + <u>pred2[,2]</u> <b># seasonal</b> effects
# plot(m2$\$$gam, scale = 0) # plot pure effects
# Convert the 2 columns (Year and Month/variable) to R Date object
# df_time <- as.Date(paste(as.numeric(l.sort$\$$Year), as.numeric(l.sort$\$$variable), "1", sep="-")); df_time
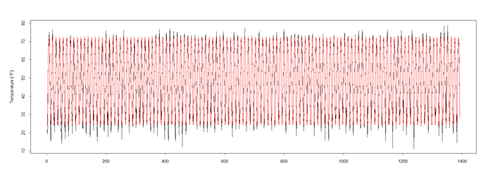
plot(x=df_time, y=l.sort$\$$temperature, data = l.sort, type = "l", xlim=c(as.Date("1950-02-01"),as.Date("1960-01-01")), xlab = "year", ylab = expression(Temperature ~ (degree*F)))
lines(x=df_time, y=pred_trend2, data = l.sort, col = "red", lwd = 2);
lines(x=df_time, y=pred_season2, data = l.sort, col = "blue", lwd = 2)
<center>[[Image:SMHS_TimeSeries14.png|500px]]</center>
==='"`UNIQ--h-4--QINU`"'Moving average smoothing===
A moving average of order $m=2k+1$ can be expressed as:
$T_{t}=\frac{1}{2k+1}\sum_{j=-k}^{k}Y_{t+j}$ .
The ''m''-MA represents an order m moving average, $T_t$, or the estimate of the trend-cycle at time ''t'', obtained by averaging values of the time series within ''k'' periods (left and right) of ''t''. This averaging process denoises the data (eliminates randomness in the data) and produces a smoother trend-cycle component.
The 5-MA contains the values of $T_t$ with ''k''=2. To see what the trend-cycle estimate looks like, we plot it along with the original data
# print the moving average results (k=3 ↔ m=7)
# library("forecast")
plot(l.sort$\$$temperature, data = l.sort, type = "l", main=" UMich/AA Temp (1900-2015) ", ylab=" Temperature (F)", xlab="Year")
lines(ma(l.sort$\$$temperature, 12), col="red", lwd=5)
lines(ma(l.sort$\$$temperature, 36), col="blue", lwd=3)
legend(0, 80, # places a legend at the appropriate place
c("Raw", "k=12 smoother", "k=36 smoothest"), # puts text in the legend
lty=c(1,1,1), # gives the legend appropriate symbols (lines)
cex=1.0, # label sizes
lwd=c(2.5,2.5), col=c("black", "red", "blue")) # gives the legend lines the correct color and width
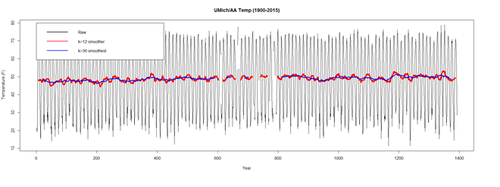
The blue trend (k=36) (3 yrs) is smoother than the original (raw) data (black) and the 1-yr average (k=12). It captures the main movement of the time series without all the minor fluctuations. We can’t estimate $T_t$ where t is close to the ends as there is not enough data there to compute the averages. The red trend (k=12) is smoother than the original (raw) data (black) but more jagged than the 3-yr average. The order of the moving average (m) determines the smoothness of the trend-cycle estimate. A larger order implies a smoother curve.
Simulation of a time-series analysis and prediction
(1) Simulate a time series
# the ts() function converts a numeric vector into an R time series object.
# format is ts(vector, start=, end=, frequency=) where start and end are the times of the first and last observation
# and frequency is the number of observations per unit time (1=annual, 4=quarterly, 12=monthly, etc.)
Note that ling Rate = $\frac{1}{Frequency}$
# save a numeric vector containing 16-years (192 monthly) observations
# from Jan 2000 to Dec 2015 as a time series object
sim_ts <- ts(as.integer(runif(192,0,10)), start=c(2000, 1), end=c(2015, 12), frequency=12)
sim_ts
# subset the time series (June 2014 to December 2015)
sim_ts2 <- window(sim_ts, start=c(2014, 6), end=c(2015, 12))
sim_ts2
# plot series
plot(sim_ts)
lines(sim_ts2, col="blue", lwd=3)
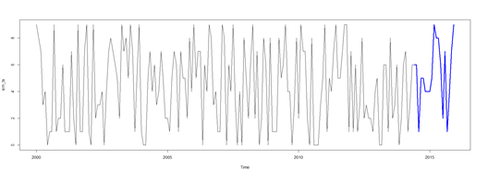
Seasonal Decomposition
- The additive and seasonal trends, and irregular components, of time-series may be decomposed using the stl() function. Series with multiplicative effects can by transformed into series with additive effects through a log transformation (i.e., ln_sim_ts <- log(sim_ts)).
# Seasonal decomposition fit_stl <- stl(sim_ts, s.window="period") # Seasonal Decomposition of Time Series by Loess plot(fit_stl) # inspect the distribution of the residuals hist(fit_stl$\$$time.series[,3]); # this contains the residuals: fit_stl$\$$time.series [,"remainder"], or seasonal, trend
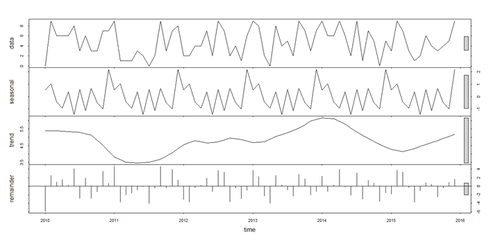
# additional plots monthplot(sim_ts) # plots the seasonal subseries of a time series. For each season, a time series is plotted. # library(forecast) seasonplot(sim_ts)
Exponential Models
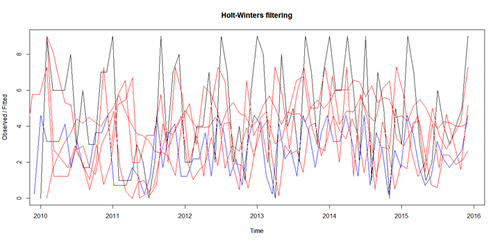
- The HoltWinters() function (stats package), and the ets() function (forecast package) can fit exponential models.
# simple exponential - models level fit_HW <- HoltWinters(sim_ts, beta=FALSE, gamma=FALSE) # double exponential - models level and trend fit_HW2<- HoltWinters(sim_ts, gamma=FALSE) # triple exponential - models level, trend, and seasonal components fit_HW3 <- HoltWinters(sim_ts) plot(fit_HW, col='black') par(new=TRUE) plot(fit_HW2, ann=FALSE, axes=FALSE, col='blue') par(new=TRUE) plot(fit_HW3, axes=FALSE, col='red') # clear plot: # dev.off()
Auto-regressive Integrated Moving Average (ARIMA) Models4
There are 2 types of ARIMA time-series models:
$ X_t= \mu+ \underbrace{\sum_{i=1}^{p}{φ_iX_{t-i}}}_\text{auto-regressive (p) part} +
\underbrace{\sum_{j=1}^{q}{θ_jε_{t-j}}}_\text{moving-average (q) part} +
\underbrace{ ε_t }_\text{error term}.$
Non-seasonal ARIMA models
The Non-seasonal ARIMA models are denoted by ARIMA(p, d, q), where parameters p, d, and q are positive integers,
- p = order of the auto-regressive model,
- d = degree of differencing, when d=2, the dth difference is $(X_t-X_{t-1})-(X_{t-1}-X_{t-2})= X_t-2X_{t-1}+X_{t-2}$. That is, the second difference of X (d=2) is not the difference between the current period and the value 2 periods ago. It is the first-difference-of-the-first difference, the discrete analog of a second derivative, representing the local acceleration of the series rather than its local trend (first derivative).
- q = order of the moving-average model.
Seasonal ARIMA models
The Seasonal AMIMA models are denoted by ARIMA(p, d, q)(P, D, Q)m,
- m = number of periods in each season,
- uppercase P, D, Q represent the auto-regressive, differencing, and moving average terms for the seasonal part of the ARIMA model, and the lower case (p,d,q) are as with non-seasonal ARIMA.
If 2 of the 3 terms are trivial, the model is abbreviated using the non-zero parameter, skipping the "AR", "I" or "MA" from the acronym. For example,
- ARIMA(1,0,0) = AR(1), a stationary and auto-correlated series can be predicted as a multiple of its own previous value, plus a constant. $X_t=μ + φ_1 × X_{t-1}+ \epsilon_t.$ Note that $ε_t=X_t-\hat{X}_t.$
- An ARIMA(0,1,0) = I(1) model, not stationary series, a limiting case of an AR(1) model, the auto-regressive coefficient is equal to 1, i.e., a series with infinitely slow mean reversion, $X_t=μ+X_{t-1}+ε_t,$ a 1-step random walk.
For more complex models:
- An ARIMA(1,1,0), differenced first-order auto-regressive model. $X_t=μ+X_{t-1}+α×(X_{t-1}-X_{t-2})+ε_t.$
- An ARIMA(0,2,2) model is given by $X_t=2X_{t-1}-X_{t-2}+α×ε_{t-1}+β×ε_{t-2}+ ε_t,$ where $α$ and $β$ are the MA(1) and MA(2) coefficients (sometimes these are defined with negative signs). This is a general linear exponential smoothing model that uses exponentially weighted moving averages to estimate both a local level and a local trend in the series. The long-term forecasts from this model converge to a straight line whose slope depends on the average trend observed toward the end of the series.
- ARIMA(1,1,2), $X_t=μ+X_{t-1}+(X_{t-1}+X_{t-2})+α×ε{t}+β×ε_{t-1}$
The arima() function (stats package) can be used to fit an auto-regressive integrated moving averages model. Other useful functions include:
- lag(sim_ts, k) lagged version of time series, shifted back k observations
- diff(sim_ts, differences=d) difference the time series d times
- ndiffs(sim_ts) Number of differences required to achieve stationarity (from the forecast package)
- acf(sim_ts) auto-correlation function
- pacf(sim_ts) partial auto-correlation function
- adf.test(sim_ts) Augmented Dickey-Fuller test. Rejecting the null hypothesis suggests that a time series is stationary (from the tseries package)
- Box.test(x, type="Ljung-Box") Portmanteau test that observations in vector or time series x are independent.
The forecast package has alternative versions of acf() and pacf() called Acf() and Pacf() respectively. # fit an ARIMA(P, D, Q) model of order:
- P, represents the AR order<
- D, represents the degree of differencing
- Q, represents the MA order.
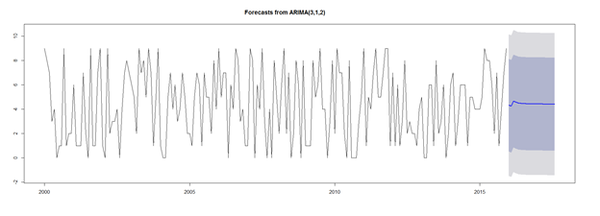
fit_arima1 <- arima(sim_ts, order=c(3, 1, 2)) # predictive accuracy library(forecast) accuracy(fit_arima1) # predict next 20 observations library(forecast) forecast(fit_arima1, 20) plot(forecast(fit_arima1, 20))
Automated Forecasting
The forecast package provides functions for the automatic selection of exponential and ARIMA models. The ets() (exponential TS) function supports both additive and multiplicative models. The auto.arima() function accounts for seasonal and nonseasonal ARIMA models according to criteria maximizing a cost function.
# library(forecast) # Automated forecasting using an exponential model fit_ets <- ets(sim_ts) # Automated forecasting using an ARIMA model fit_arima2 <- auto.arima(sim_ts) # Compare the AIC (model quality) for both models fit_ets$\$$aic; fit_arima2$\$$aic accuracy(fit_ets); accuracy(fit_arima2);
Akaike’s Information Criterion (AIC) = -2Log(Likelihood)+2p, where p is he number of estimated parameters.
summary(fit_ets); summary(fit_arima2)
ACF plot of the residuals from the ARIMA(3,1,2) model shows all correlations within the threshold limits indicating that the residuals are behaving like white noise. A portmanteau test returns a large p-value, also suggesting the residuals are white noise.
# acf computes (and by default plots) estimates of the autocovariance or autocorrelation function acf(residuals(fit_ets))
# Box–Pierce or Ljung–Box test statistic for examining the null hypothesis of independence in a given time series. # These are sometimes known as ‘portmanteau’ tests. Box.test(residuals(fit_ets), lag=24, fitdf=4, type="Ljung") # plot forecast plot(forecast(fit_arima2)) # more on ARIMA https://www.otexts.org/fpp/8/7
Footnotes
- 1 https://umich.instructure.com/files/689861/download?download_frd=1
- 2 https://umich.instructure.com/courses/38100/files
- 3 https://cran.r-project.org/web/packages/mgcv/mgcv.pdf
- 4 http://arxiv.org/ftp/arxiv/papers/1302/1302.6613.pdf
See also
- SOCR Home page: http://www.socr.ucla.edu
"-----
Translate this page: