Difference between revisions of "UQuadraticDistribuionAbout"
m |
|||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 10: | Line 10: | ||
<center>(vertical scale) <math>\alpha = {12 \over \left ( b-a \right )^3}</math>. | <center>(vertical scale) <math>\alpha = {12 \over \left ( b-a \right )^3}</math>. | ||
</center> | </center> | ||
| − | + | More information about U-quadratic, and other continuous distribution functions, is available at [http://en.wikipedia.org/wiki/UQuadratic_distribution Wikipedia]. | |
===Properties=== | ===Properties=== | ||
* Support Parameters: <math>a < b \in (-\infty,\infty)</math> | * Support Parameters: <math>a < b \in (-\infty,\infty)</math> | ||
| − | * | + | * Scale/Offset Parameters: <math>\alpha \in (0,\infty)</math> and <math>\beta \in (-\infty,\infty)</math> |
* PDF: <math>f(x)=\alpha \left ( x - \beta \right )^2, \forall x \in [a , b]</math> | * PDF: <math>f(x)=\alpha \left ( x - \beta \right )^2, \forall x \in [a , b]</math> | ||
* CDF <math>F(x)={\alpha \over 3} \left ( (x - \beta)^3 + (\beta - a)^3 \right ), \forall x \in [a , b]</math> | * CDF <math>F(x)={\alpha \over 3} \left ( (x - \beta)^3 + (\beta - a)^3 \right ), \forall x \in [a , b]</math> | ||
| Line 23: | Line 23: | ||
* Skewness: 0 (distribution is symmetric around the mean) | * Skewness: 0 (distribution is symmetric around the mean) | ||
* Kurtosis: <math> {3 \over 112} (b-a)^4 </math> | * Kurtosis: <math> {3 \over 112} (b-a)^4 </math> | ||
| + | * Moment Generating Function: <math>M_x(t)= {-3\left(e^{at}(4+(a^2+2a(-2+b)+b^2)t)- e^{bt} (4 + (-4b + (a+b)^2)t)\right) \over (a-b)^3 t^2 }</math> | ||
| + | * Characteristic Function: <math>{3i\left(e^{iat}(-4i+(a^2+2a(-2+b)+b^2)t)+ e^{ibt} (4i - (-4b + (a+b)^2)t)\right) \over (a-b)^3 t^2 }</math> | ||
===Interactive U Quadratic Distribution=== | ===Interactive U Quadratic Distribution=== | ||
| − | You can see the interactive ''U Quadratic'' distribution by going to [http://socr.ucla.edu/htmls/ | + | You can see the interactive ''U Quadratic'' distribution by going to [http://socr.ucla.edu/htmls/dist/UQuadratic_Distribution.html SOCR Distributions] and selecting from the drop down list of distributions ''U Quadratic''. Then follow the '''Help''' instructions to dynamically set parameters, compute critical and probability values using the mouse and keyboard. |
<center>[[Image:SOCR_Distributions_UQuadraticAbout_Dinov_Fig2.jpg|500px]]</center> | <center>[[Image:SOCR_Distributions_UQuadraticAbout_Dinov_Fig2.jpg|500px]]</center> | ||
| Line 31: | Line 33: | ||
<hr> | <hr> | ||
* SOCR Home page: http://www.socr.ucla.edu | * SOCR Home page: http://www.socr.ucla.edu | ||
| + | * [http://en.wikipedia.org/wiki/U-quadratic_distribution U-quadratic distribution at Wikipedia] | ||
{{translate|pageName=http://wiki.stat.ucla.edu/socr/index.php?title=UQuadraticDistribuionAbout}} | {{translate|pageName=http://wiki.stat.ucla.edu/socr/index.php?title=UQuadraticDistribuionAbout}} | ||
Latest revision as of 14:15, 28 December 2009
Contents
About_pages_for_SOCR_Distributions - U-Quadratic Distribution
Description
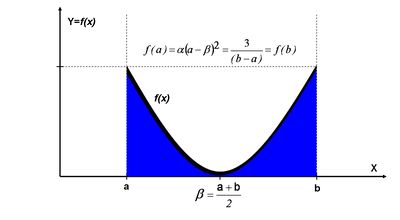
The U quadratic distribution is defined by the following density function
where the relation between the two pairs of parameters (domain-support, a and b) and (range/offset \(\alpha\) and \(\beta\)) are given by the following two equations
More information about U-quadratic, and other continuous distribution functions, is available at Wikipedia.
Properties
- Support Parameters\[a < b \in (-\infty,\infty)\]
- Scale/Offset Parameters\[\alpha \in (0,\infty)\] and \(\beta \in (-\infty,\infty)\)
- PDF\[f(x)=\alpha \left ( x - \beta \right )^2, \forall x \in [a , b]\]
- CDF \(F(x)={\alpha \over 3} \left ( (x - \beta)^3 + (\beta - a)^3 \right ), \forall x \in [a , b]\)
- Mean\[{a+b \over 2}\]
- Median\[{a+b \over 2}\]
- Modes\[a \] and \( b \)
- Variance\[ {3 \over 20} (b-a)^2 \]
- Skewness: 0 (distribution is symmetric around the mean)
- Kurtosis\[ {3 \over 112} (b-a)^4 \]
- Moment Generating Function\[M_x(t)= {-3\left(e^{at}(4+(a^2+2a(-2+b)+b^2)t)- e^{bt} (4 + (-4b + (a+b)^2)t)\right) \over (a-b)^3 t^2 }\]
- Characteristic Function\[{3i\left(e^{iat}(-4i+(a^2+2a(-2+b)+b^2)t)+ e^{ibt} (4i - (-4b + (a+b)^2)t)\right) \over (a-b)^3 t^2 }\]
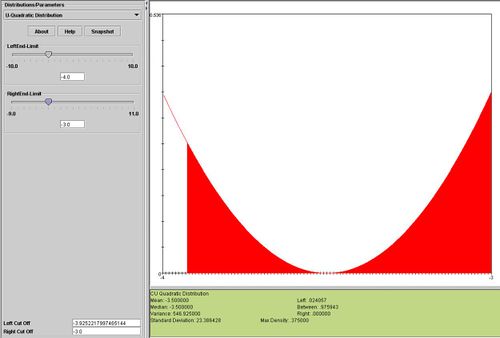
Interactive U Quadratic Distribution
You can see the interactive U Quadratic distribution by going to SOCR Distributions and selecting from the drop down list of distributions U Quadratic. Then follow the Help instructions to dynamically set parameters, compute critical and probability values using the mouse and keyboard.
- SOCR Home page: http://www.socr.ucla.edu
- U-quadratic distribution at Wikipedia
Translate this page: