Difference between revisions of "EBook Problems MultivariateNormal"
(→EBook Problems Set - Mutivariate Normal Distribution) |
(→EBook Problems Set - Mutivariate Normal Distribution) |
||
| Line 194: | Line 194: | ||
}} | }} | ||
| + | ===Problem 3=== | ||
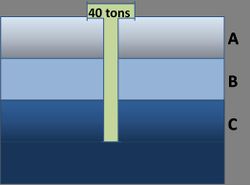
| + | A friction pile is driven through three soil layers as shown in the following figure: | ||
| + | [[Image:Problem 3.jpg|250x250px|center]] | ||
| + | The total bearing capacity of the friction pile (in tons) is obtained from | ||
| + | |||
| + | <math> | ||
| + | Q=4A+B+2C | ||
| + | </math> | ||
| + | |||
| + | Where A, B, and C are penetration lengths (in meters) through each of the three soil layers, respectively. Suppose A ~ N(5,3); B ~ N(8,2); A and B are negatively correlated with coefficient <math>\rho</math> = - 0.5. The total length of the pile is 30 meters. Determine the probability that the pile will fail to support the 40 ton load, i.e., the event that the capacity Q is less than 40 tons. [Hint: Observe C = 30 - (A+B)]. | ||
| + | |||
| + | {{hidden|Answer| | ||
| + | <math> | ||
| + | Q=4A+B+2C \, | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | =4A+B+2(30-A-B) \, | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | =2A-B+60 \, | ||
| + | </math> | ||
| + | |||
| + | Hence, | ||
| + | |||
| + | <math> | ||
| + | \mu_Q=2 x 5-8+60=62 \, | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | \sigma_Q=[4 x 3^2+1 x 2^2 +2(2)(-1)(-0.5)(3)(2)]^{1/2} \, | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | =(36+4+12)^{1/2}=\sqrt{52} \, | ||
| + | </math> | ||
| + | |||
| + | Hence | ||
| + | |||
| + | <math> | ||
| + | P(Q<40)=P(\frac{Q-\mu_Q}{\sigma_Q}<\frac{40-62}{\sqrt{52}}) \, | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | =\Phi(-3.050851079) \, | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | \cong0.00114 \, | ||
| + | </math> | ||
| + | |||
| + | }} | ||
<hr> | <hr> | ||
Revision as of 20:14, 13 January 2011
Contents
EBook Problems Set - Mutivariate Normal Distribution
Problem 1
Person1 and Person2 are travelling from point A to point D, but there are different routes to get from A to D. Person1 decides to take the A->B->D route, whereas Person2 takes the A->C->D route.
The travel times (in hours) between each pair of points indicated are normally distributed as follows:
T1 ~ N (6, 2)
T2 ~ N (4, 1)
T3 ~ N (5, 3)
T4 ~ N (4, 1)
Explain why these times are stochastic (and not exact or deterministic)? Although the travel times here generally can be assumed statistically independent, T3 and T4 are dependent with correlation coefficient 0.8.
(a) What is the probability that Person2 will not arrive at point D within 10 hours?
(b) What is the probability that Person1 will arrive at point D earlier than Person2 by at least one hour?
(c) Which route (A\(\rightarrow\)B\(\rightarrow\)D or A\(\rightarrow\)C\(\rightarrow\)D) should be taken if one wishes to minimize the expected travel time from A to D? Explain.
{\sigma_{T2}}\leq\frac{10-9}{3.847076812})
=1-\Phi(0.259937622)=1-0.602543999
\cong 0.397 \) }}
) \, \)
Hence
\( =\Phi (-0.44946657) \, \)
\( \cong 0.327 \, \) }}
Problem 2
The settlement (in cm) of a structure shown in the following figure may be evaluated from
\( S=0.3A+0.2B+0.1C \)
where A, B, and C are respectively the thickness (in m) of the three layers of soil as shown. Suppose A, B, and C are modeled as independent normal random variables as
A ~ N(5,1)
B ~ N(8,2)
C ~ N(7,1)
(a) Determine the probability that the settlement will exceed 4 cm.
(b) If the total thickness of the three layers is known exactly as 20 m; and furthermore, thicknesses A and B are correlated with correlation coefficient equal to 0.5, determine the probability that the settlement will exceed 4 cm.
) \, \)
\( =1-\Phi(0.57735027)=1-0.718148613 \cong 0.282 \, \) }}
Problem 3
A friction pile is driven through three soil layers as shown in the following figure:
The total bearing capacity of the friction pile (in tons) is obtained from
\( Q=4A+B+2C \)
Where A, B, and C are penetration lengths (in meters) through each of the three soil layers, respectively. Suppose A ~ N(5,3); B ~ N(8,2); A and B are negatively correlated with coefficient \(\rho\) = - 0.5. The total length of the pile is 30 meters. Determine the probability that the pile will fail to support the 40 ton load, i.e., the event that the capacity Q is less than 40 tons. [Hint: Observe C = 30 - (A+B)].
) \, \)
\( =\Phi(-3.050851079) \, \)
\( \cong0.00114 \, \)
}}
- Back to Ebook
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: