Difference between revisions of "SMHS ANOVA"
(→Theory) |
|||
| Line 51: | Line 51: | ||
*Calculations: | *Calculations: | ||
| − | + | <center> | |
| − | + | {| class="wikitable" style="text-align:center; width:50%" border="1" | |
| − | + | |- | |
| − | + | | Variance Source || Degrees of Freedom (df) || Sum of Squares (SS) || Mean Sum of Squares (MS) || F-Statistics || [http://socr.ucla.edu/htmls/SOCR_Distributions.html P-value] | |
| − | + | |- | |
| − | + | | Treatment Effect (Between Group) || k-1 || <math>\sum_{i=1}^{k}{n_i(\bar{y}_{i,.}-\bar{y})^2}</math> || <math>MST(Between)={SST(Between)\over df(Between)}</math> || <math>F_o = {MST(Between)\over MSE(Within)}</math> || <math>P(F_{(df(Between), df(Within))} > F_o)</math> | |
| − | + | |- | |
| − | + | | Error (Within Group) || n-k || <math>\sum_{i=1}^{k}{\sum_{j=1}^{n_i}{(y_{i,j}-\bar{y}_{i,.})^2}}</math> || <math>MSE(Within)={SSE(Within)\over df(Within)}</math> || || [http://socr.ucla.edu/Applets.dir/Normal_T_Chi2_F_Tables.htm F-Distribution Calculator] | |
| − | + | |- | |
| − | + | | Total || n-1 || <math>\sum_{i=1}^{k}{\sum_{j=1}^{n_i}{(y_{i,j} - \bar{y})^2}}</math> || || || [[SOCR_EduMaterials_AnalysisActivities_ANOVA_1 | ANOVA Activity]] | |
| + | |} | ||
| + | </center> | ||
ANOVA hypotheses (general form): $H_{\sigma}:\mu_{1}=\mu_{2}=⋯=\mu_{k}$; $H_{a}:\mu_{I}≠\mu_{j}$ for some $i≠j$. The test statistics: $F_{0}=\frac{MST(between)}{MSE(within)}$ , if $F_{0}$ is large, then there is a lot between group variation, relative to the within group variation. Therefore, the discrepancies between the group means are large compared to the variability within the groups (error). That is large $F_{0}$ provides strong evidence against $H_{0}$. | ANOVA hypotheses (general form): $H_{\sigma}:\mu_{1}=\mu_{2}=⋯=\mu_{k}$; $H_{a}:\mu_{I}≠\mu_{j}$ for some $i≠j$. The test statistics: $F_{0}=\frac{MST(between)}{MSE(within)}$ , if $F_{0}$ is large, then there is a lot between group variation, relative to the within group variation. Therefore, the discrepancies between the group means are large compared to the variability within the groups (error). That is large $F_{0}$ provides strong evidence against $H_{0}$. | ||
| Line 87: | Line 89: | ||
</center> | </center> | ||
| − | + | Using this data, we have the following ANOVA table: | |
| − | + | <center> | |
| − | + | {| class="wikitable" style="text-align:center; width:50%" border="1" | |
| − | + | |- | |
| − | + | | Variance Source || Degrees of Freedom (df) || Sum of Squares (SS) || Mean Sum of Squares (MS) || F-Statistics || [http://socr.ucla.edu/htmls/dist/Fisher_Distribution.html P-value] | |
| − | + | |- | |
| − | + | | Treatment Effect (Between Group) || 3-1 || <math>\sum_{i=1}^{k}{n_i(\bar{y}_{i,.}-\bar{y})^2}=19.86</math> || <math>{SST(Between)\over df(Between)}={19.86\over 2}</math> || <math>F_o = {MST(Between)\over MSE(Within)}=13.24</math> || <math>P(F_{(df(Between), df(Within))} > F_o)=0.017</math> | |
| − | + | |- | |
| + | | Error (Within Group) || 7-3 || <math>\sum_{i=1}^{k}{\sum_{j=1}^{n_i}{(y_{i,j}-\bar{y}_{i,.})^2}}=3</math> || <math>{SSE(Within)\over df(Within)}={3\over 4}</math> || || [http://socr.ucla.edu/Applets.dir/Normal_T_Chi2_F_Tables.htm F-Distribution Calculator] | ||
| + | |- | ||
| + | | Total || 7-1 || <math>\sum_{i=1}^{k}{\sum_{j=1}^{n_i}{(y_{i,j} - \bar{y})^2}}=22.86</math> || || || [[SOCR_EduMaterials_AnalysisActivities_ANOVA_1 | Anova Activity]] | ||
| + | |} | ||
| + | </center> | ||
Based on the ANOVA table above, we can reject the null hypothesis at $\alpha=0.05.$ | Based on the ANOVA table above, we can reject the null hypothesis at $\alpha=0.05.$ | ||
| Line 118: | Line 125: | ||
*Calculations: | *Calculations: | ||
| − | + | It is assumed that main effect A has ''a'' levels (and df(A) = a-1), main effect B has ''b'' levels (and (df(B) = b-1), ''r'' is the sample size of each treatment, and <math>N = a\times b\times n</math> is the total sample size. Notice the overall degree of freedom is once again one less than the total sample size. | |
| + | |||
| + | <center> | ||
| + | {| class="wikitable" style="text-align:center; width:50%" border="1" | ||
| + | |- | ||
| + | | Variance Source || Degrees of Freedom (df) || Sum of Squares (SS) || Mean Sum of Squares (MS) || F-Statistics || [http://socr.umich.edu/html/dist/ P-value] | ||
| + | |- | ||
| + | | Main Effect A || df(A)=a-1 || <math>SS(A)=r\times b\times\sum_{i=1}^{a}{(\bar{y}_{i,.,.}-\bar{y})^2}</math> || <math>{SS(A)\over df(A)}</math> || <math>F_o = {MS(A)\over MSE}</math> || <math>P(F_{(df(A), df(E))} > F_o)</math> | ||
| + | |- | ||
| + | | Main Effect B || df(B)=b-1 || <math>SS(B)=r\times a\times\sum_{j=1}^{b}{(\bar{y}_{., j,.}-\bar{y})^2}</math> || <math>{SS(B)\over df(B)}</math> || <math>F_o = {MS(B)\over MSE}</math> || <math>P(F_{(df(B), df(E))} > F_o)</math> | ||
| + | |- | ||
| + | | A vs.B Interaction || df(AB)=(a-1)(b-1) || <math>SS(AB)=r\times \sum_{i=1}^{a}{\sum_{j=1}^{b}{((\bar{y}_{i, j,.}-\bar{y}_{i, .,.})+(\bar{y}_{., j,.}-\bar{y}))^2}}</math> || <math>{SS(AB)\over df(AB)}</math> || <math>F_o = {MS(AB)\over MSE}</math> || <math>P(F_{(df(AB), df(E))} > F_o)</math> | ||
| + | |- | ||
| + | | Error || <math>N-a\times b</math> || <math>SSE=\sum_{k=1}^r{\sum_{i=1}^{a}{\sum_{j=1}^{b}{(\bar{y}_{i, j,k}-\bar{y}_{i, j,.})^2}}}</math> || <math>{SSE\over df(Error)}</math> || || | ||
| + | |- | ||
| + | | Total || N-1 || <math>SST=\sum_{k=1}^r{\sum_{i=1}^{a}{\sum_{j=1}^{b}{(\bar{y}_{i, j,k}-\bar{y}_{., .,.})^2}}}</math> || || || [[SOCR_EduMaterials_AnalysisActivities_ANOVA_2 | ANOVA Activity]] | ||
| + | |} | ||
| + | </center> | ||
[[Image:ANOVA_Figure_3_under_Calculations.png |500px]] | [[Image:ANOVA_Figure_3_under_Calculations.png |500px]] | ||
Revision as of 09:02, 28 August 2014
Contents
Scientific Methods for Health Sciences - Analysis of Variance (ANOVA)
Overview
Analysis of Variance (ANOVA) is the common method applied to analyze the differences between group means. In ANOVA, we divide the observed variance into components attributed to different sources of variation. It is widely used statistical technique which provides a statistical test of whether or not the means of several groups are equal, that is ANOVA can be thought as a generalized t-test for more than 2 groups (ANOVA results in the case of 2 groups coincide with the corresponding results of a 2-sample independent t-test). Here we introduce the ANOVA method, specifically one-way ANOVA and two-way ANOVA, with examples.
Motivation
In the previous two-sample inference, we applied the independent t-test to compare two independent group means. What if we want to compare k (k>2) independent samples? In this case, we will need to decompose the entire variation into components allowing us to analyze the variance of the entire dataset. Suppose 5 varieties of products are tested for further study. A filed was divided into 20 plots, with each variety planted in four plots. The measurements are shown in the table below:
| A | B | C | D | E |
| 26.2 | 29.2 | 29.1 | 21.3 | 20.1 |
| 24.3 | 28.1 | 30.8 | 22.4 | 19.3 |
| 21.8 | 27.3 | 33.9 | 24.3 | 19.9 |
| 28.1 | 31.2 | 32.8 | 21.8 | 22.1 |
| A | 26.2,24.3,21.8,28.1 |
| B | 29.2,28.1,27.3,31.2 |
| C | 29.1,30.8,33.9,32.8 |
| D | 21.3,22.4,24.3,21.8 |
| E | 20.1,19.3,19.9,22.1 |
Using ANOVA, the data are regarded as random samples from k populations. Suppose the population means of the sample are denoted as $\mu_{1},\mu_{2},\mu_{3},\mu_{4},\mu_{5}$and their population standard deviation are denoted as $\sigma_{1},\sigma_{2},\sigma_{3},\sigma_{4},\sigma_{5}$. An obvious method is to do $\binom{5}{2}=10$ separate t-tests and compare all independent pairs of groups. In this case, ANOVA would be much easier and powerful.
Theory
One-way ANOVA: we expand our inference methods to study and compare k independent samples. In this case, we will be decomposing the entire variation in the data into independent components.
- Notations first: $y_{ij}$ is the measurement from group $i$, observation index $j$; $k$ is the number of groups; $n_{i}$ is the number of observations in group $i$; $n$ is the total number of observations and $n=n_{1}+n_{2}+⋯+n_{k}$. The group mean for group $i$ is $\bar y_{l}$=$\frac{\sum_{j=1}^{n_{i}} y_{ij}} {n_{i}}$, the grand mean is $\bar y =\bar y_{..}=$ $\frac{\sum_{i=1}^{k}\sum_{j=1}^{n}_{i}y_{ij}}{n}$
- Difference between the means (compare each group mean to the grand mean): total variance $SST(total)=\sum_{i=1}^{k}\sum_{j=1}^{n_i}(y_{ij}-(\bar y_{..})^{2}$, degrees of freedom $df(total)=n-1$; difference between each group mean and grand mean: $SST(between)$=$\sum_{i=1}^{k} \sum_{j=1}^{n_i}(y_{ij}-\bar y_{..})^{2}$, degrees of freedom $df(between)=k-1$; Sum square due to error (combination of variation within group):$SSE=\sum_{i=1}^{k} n_{i}(\bar y_{l.}- \bar y_{..})^2$, $degrees\, of\, freedom$ $df(within)=n-k$. With ANOVA decomposition, we have $\sum_{i=1}^{k} \sum_{j=1}^{n_{i}}(y_{ij}-(\bar y_{..})^{2}$ $\sum_{i=1}^{k} n_{i} (y_{l.}-(bar y_{..})^{2}$ $\sum_{i=1}^{k} \sum_{j=1}^{n_i}(y_{ij}-(\bar y_{l.})^{2},$ that is $SST(total)$=$SST(between)$+$SSE(within)$and $df(total)$=$df(between)$+$df(within).$
- Calculations:
| Variance Source | Degrees of Freedom (df) | Sum of Squares (SS) | Mean Sum of Squares (MS) | F-Statistics | P-value |
| Treatment Effect (Between Group) | k-1 | \(\sum_{i=1}^{k}{n_i(\bar{y}_{i,.}-\bar{y})^2}\) | \(MST(Between)={SST(Between)\over df(Between)}\) | \(F_o = {MST(Between)\over MSE(Within)}\) | \(P(F_{(df(Between), df(Within))} > F_o)\) |
| Error (Within Group) | n-k | \(\sum_{i=1}^{k}{\sum_{j=1}^{n_i}{(y_{i,j}-\bar{y}_{i,.})^2}}\) | \(MSE(Within)={SSE(Within)\over df(Within)}\) | F-Distribution Calculator | |
| Total | n-1 | \(\sum_{i=1}^{k}{\sum_{j=1}^{n_i}{(y_{i,j} - \bar{y})^2}}\) | ANOVA Activity |
ANOVA hypotheses (general form): $H_{\sigma}:\mu_{1}=\mu_{2}=⋯=\mu_{k}$; $H_{a}:\mu_{I}≠\mu_{j}$ for some $i≠j$. The test statistics: $F_{0}=\frac{MST(between)}{MSE(within)}$ , if $F_{0}$ is large, then there is a lot between group variation, relative to the within group variation. Therefore, the discrepancies between the group means are large compared to the variability within the groups (error). That is large $F_{0}$ provides strong evidence against $H_{0}$.
- Examples: given the following data from a hands-on study.
| Groups | |||
| Index | A | B | C |
| 1 | 0 | 1 | 4 |
| 2 | 1 | 0 | 5 |
| 3 | 2 | ||
| $n_{i}$ | 2 | 3 | 2 |
| $s$ | 1 | 3 | 9 |
| $\bar y_{l}$ | 0.5 | 1 | 4.5 |
Using this data, we have the following ANOVA table:
| Variance Source | Degrees of Freedom (df) | Sum of Squares (SS) | Mean Sum of Squares (MS) | F-Statistics | P-value |
| Treatment Effect (Between Group) | 3-1 | \(\sum_{i=1}^{k}{n_i(\bar{y}_{i,.}-\bar{y})^2}=19.86\) | \({SST(Between)\over df(Between)}={19.86\over 2}\) | \(F_o = {MST(Between)\over MSE(Within)}=13.24\) | \(P(F_{(df(Between), df(Within))} > F_o)=0.017\) |
| Error (Within Group) | 7-3 | \(\sum_{i=1}^{k}{\sum_{j=1}^{n_i}{(y_{i,j}-\bar{y}_{i,.})^2}}=3\) | \({SSE(Within)\over df(Within)}={3\over 4}\) | F-Distribution Calculator | |
| Total | 7-1 | \(\sum_{i=1}^{k}{\sum_{j=1}^{n_i}{(y_{i,j} - \bar{y})^2}}=22.86\) | Anova Activity |
Based on the ANOVA table above, we can reject the null hypothesis at $\alpha=0.05.$
- ANOVA conditions: valid if (1) design conditions: all groups of observations represent random samples from their population respectively. Plus, all the observations within each group are independent of each other; (2) population conditions: the k population distributions must be approximately normal. If sample size is large, the normality condition is less crucial. Plus, the standard deviations of all populations are equal, which can be slightly relaxed when $0.5≤\frac{\sigma_{i}}{\sigma_{j}}≤2,$ for all $i$ and $j$, none of the population variance is twice larger than any of the other ones.
- Two-way ANOVA: we focus on decomposing the variance of a dataset into independent (orthogonal) components when we have two grouping factors.
Notations first: two-way model:$y_{ijk}=\mu+\tau_{i}+\beta_{j}+γ_{ij}+\varepsilon_{ijk},$ for all $1≤i≤a,1≤j≤b$ and $1≤k≤r.$ $y_{ijk}$ is the A-factor level $i$, and B-factor level $j$, observation-index $k$ measurement; $k$ is the number of replications; $a_{i}$ is the number of A-factor observations at level $i,a=a_{1}+⋯+a_{I}$; $b_{j}$ is the number of B-factor observations at level $j$,$b=b_{1}+⋯+b_{J}$; $N$ is the total number of observations and $N=a*a*b$. Here $\mu$ is the overall mean response, $\tau_{i}$ is the effect due to the $i^{th}$ level of factor A, $\beta_{j}$ is the effect due to the $j^{th}$ level of factor B, and $\gamma_{ij}$ is the effect due to any interaction between the $i^{th}$ level of factor A and $j^{th}$ level of factor B. The mean for A-factor group mean at level $I$ and B-factor at level $j$ is $\bar y_{ij}=\frac{\sum_{k=1}^{r} y_{ijk}} {r},$ the grand mean is$\bar y =$
- Hypotheses:
- Null hypotheses: (1) the population means of the first factor are equal, which is like the one-way ANOVA for the row factor; (2) the population means of the second factor are equal, which is like the one-way ANOVA for the column factor; (3) there is no interaction between the two factors, which is similar to performing a test for independence with contingency tables.
- Factors: factor A and factor B are independent variables in two-way ANOVA.
- Treatment groups: formed by making all possible combinations of two factors. For example, if the factor A has 3 levels and factor B has 5 levels, then there will be 3*5=15 different treatment groups.
- Main effect: involves the dependent variable one at a time. The interaction is ignored for this part.
- Interaction effect: the effect that one factor has on the other factor. The degree of freedom is the product of the two degrees of freedom of each factor.
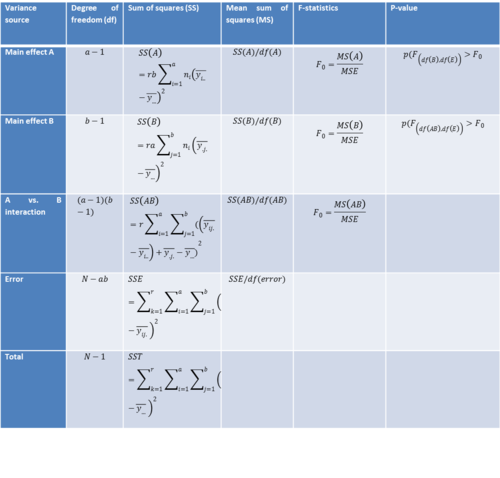
- Calculations:
It is assumed that main effect A has a levels (and df(A) = a-1), main effect B has b levels (and (df(B) = b-1), r is the sample size of each treatment, and \(N = a\times b\times n\) is the total sample size. Notice the overall degree of freedom is once again one less than the total sample size.
| Variance Source | Degrees of Freedom (df) | Sum of Squares (SS) | Mean Sum of Squares (MS) | F-Statistics | P-value |
| Main Effect A | df(A)=a-1 | \(SS(A)=r\times b\times\sum_{i=1}^{a}{(\bar{y}_{i,.,.}-\bar{y})^2}\) | \({SS(A)\over df(A)}\) | \(F_o = {MS(A)\over MSE}\) | \(P(F_{(df(A), df(E))} > F_o)\) |
| Main Effect B | df(B)=b-1 | \(SS(B)=r\times a\times\sum_{j=1}^{b}{(\bar{y}_{., j,.}-\bar{y})^2}\) | \({SS(B)\over df(B)}\) | \(F_o = {MS(B)\over MSE}\) | \(P(F_{(df(B), df(E))} > F_o)\) |
| A vs.B Interaction | df(AB)=(a-1)(b-1) | \(SS(AB)=r\times \sum_{i=1}^{a}{\sum_{j=1}^{b}{((\bar{y}_{i, j,.}-\bar{y}_{i, .,.})+(\bar{y}_{., j,.}-\bar{y}))^2}}\) | \({SS(AB)\over df(AB)}\) | \(F_o = {MS(AB)\over MSE}\) | \(P(F_{(df(AB), df(E))} > F_o)\) |
| Error | \(N-a\times b\) | \(SSE=\sum_{k=1}^r{\sum_{i=1}^{a}{\sum_{j=1}^{b}{(\bar{y}_{i, j,k}-\bar{y}_{i, j,.})^2}}}\) | \({SSE\over df(Error)}\) | ||
| Total | N-1 | \(SST=\sum_{k=1}^r{\sum_{i=1}^{a}{\sum_{j=1}^{b}{(\bar{y}_{i, j,k}-\bar{y}_{., .,.})^2}}}\) | ANOVA Activity |
- SOCR Home page: http://www.socr.umich.edu
Translate this page: