SMHS BigDataBigSci SEM Ex1

Structural Equation Modeling (SEM) - Hands-on Example 1 (School Kids Mental Abilities)

These data (Holzinger & Swineford 1939) include mental ability test scores of 7 & 8 grade children from two schools (Pasteur and Grant-White). This version of the dataset includes only 9 (out of the 26) tests. We can build and test a confirmatory factor analysis (CFA) SEM model for 3 correlated latent variables (or factors), each with three indicators:

visual factor measured by 3 variables: x1, x2 and x3,

textual factor measured by 3 variables: x4, x5 and x6,

speed factor measured by 3 variables: x7, x8 and x9.

id	lhs	op	rhs	user	free	ustart
1	Visual	=~	x1	1	0	1
2	Visual	=~	x2	1	1	NA
3	Visual	=~	x3	1	2	NA
4	Textual	=~	x4	1	0	1
5	Textual	=~	x5	1	3	NA
6	Textual	=~	x6	1	4	NA
7	Speed	=~	x7	1	0	1
8	Speed	=~	x8	1	5	NA
9	Speed	=~	x9	1	6	NA
10	x1	~~	x1	0	7	NA
11	x2	~~	x2	0	8	NA
12	x3	~~	x3	0	9	NA
13	x4	~~	x4	0	10	NA
14	x5	~~	x5	0	11	NA
15	x6	~~	x6	0	12	NA
16	x7	~~	x7	0	13	NA
17	x8	~~	x8	0	14	NA
18	x9	~~	x9	0	15	47.8
19	Visual	~~	Visual	0	16	NA
20	Textual	~~	Textual	0	17	NA
21	Speed	~~	Speed	boy	18	NA
22	Visual	~~	Textual	girl	19	NA
23	Visual	~~	Speed	girl	20	NA
24	Textual	~~	Speed	boy	21	NA

There are 3 latent variables (factors) in this model, each with 3 indicators, resulting in 9 factor loadings that need to be estimated. There are also 3 covariances among the latent variables {another three parameters}.

These 12 parameters are represented in the path diagram as single-headed and double-headed arrows, respectively. We also need to estimate the residual variances of the 9 observed variables and the variances of the 3 latent variables, resulting in 12 additional free parameters. In total, we have 24 parameters.

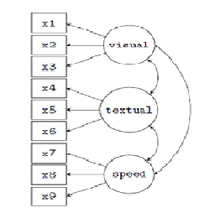
To fully identify the model we need to set the metric of the latent variables. There are 2 ways to do this:

for each latent variable, fix the factor loading of one of the indicators (typically the first) to a constant (e.g., 1.0), or

standardize the variances of the 3 latent variables.

Either way, we fix 3 of these 24 parameters, and 21 parameters remain free.

The parTable(fit) method, generates this table output.

The `rhs', `op' and `lhs' columns define the parameters of the model. All parameters with the `=~' operator are factor loadings, whereas all parameters with the `~~' operator are variances or covariances. Nonzero elements in the `free' column are the free parameters of the model. Zero elements in the `free' column correspond to fixed parameters, whose value is found in the `start' column.

Lavaan’s user-friendly model-specification approach is implemented in the fitting functions: cfa() and sem().

Since these data contain 3 latent variables, and no regressions, the minimalist syntax is:

data.model <- 'visual 	        =~ x1 + x2 + x3
textual 	                =~ x4 + x5 + x6
speed 	                        =~ x7 + x8 + x9'

Fit the CFA model:

fit.1 <- cfa(data.model, data = HolzingerSwineford1939)

The `user' column (parTabale) shows which parameters were explicitly contained in the user-specified model syntax (= 1), and which parameters were added by the cfa() function (= 0).

parTable(fit.1)

If we prefer not to fix the factor loadings of the first indicator, but instead want to fix the variances of the latent variances, the model syntax would be changed to:

fit.2 <- 'visual =~ NA*x1 + x2 + x3
textual =~ NA*x4 + x5 + x6
speed =~ NA*x7 + x8 + x9
visual ~~ 1*visual
textual ~~ 1*textual
speed ~~ 1*speed'

More complex model specifications can be made using the full lavaan model syntax:

fit.full <- '			# latent variables
visual 	=~ 1*x1 + x2 + x3
textual =~ 1*x4 + x5 + x6
speed 	=~ 1*x7 + x8 + x9
# residual variances observed variables
x1 	~~ x1
x2 	~~ x2
x3 	~~ x3
x4 	~~ x4
x5 	~~ x5
x6 	~~ x6
x7 	~~ x7
x8 	~~ x8
x9 	~~ x9
# factor variances
visual 	~~ visual
textual ~~ textual
speed 	~~ speed
# factor covariances
visual 	~~ textual + speed
textual ~~ speed'
fit.3 <- lavaan(fit.full, data = HolzingerSwineford1939)

We can specify the model where the first factor loadings are explicitly fixed to one, and the covariances among the factors are added manually.

fit.mixed <- '		# latent variables
visual =~ 1*x1 + x2 + x3
textual =~ 1*x4 + x5 + x6
speed =~ 1*x7 + x8 + x9
# factor covariances
visual ~~ textual + speed
textual ~~ speed'
fit <- lavaan(fit.mixed, data = HolzingerSwineford1939, auto.var = TRUE)

The best method to view results from a SEM fitted with lavaan is summary(), which can be called with optional arguments like fit.measures, standardized, and rsquare.

Core Lavaan Methods

summary() print a long summary of the model results

show() print a short summary of the model results

coef() returns the estimates of the free parameters in the model as a named numeric vector

fitted() returns the implied moments (covariance matrix and mean vector) of the model

resid() returns the raw, normalized or standardized residuals (difference between implied and observed moments)

vcov() returns the covariance matrix of the estimated parameters

predict() compute factor scores

logLik() returns the log-likelihood of the fitted model (if maximum likelihood estimation was used)

AIC(), BIC() compute information criteria (if maximum likelihood estimation is used)

update() update a fitted lavaan object

inspect() peek into the internal representation of the model; by default, it returns a list of model matrices counting the free parameters in the model; can also be used to extract starting values, gradient values, and much more

If these args are set to TRUE, the output includes additional fit measures, standardized estimates, and R2 values for the dependent variables, respectively

fit.model <- 'visual =~ x1 + x2 + x3
textual =~ x4 + x5 + x6
 speed =~ x7 + x8 + x9'
fit <- cfa(fit.model, data = HolzingerSwineford1939)
summary(fit, fit.measures = TRUE)

fit <- cfa(fit.model, data=HolzingerSwineford1939, estimator="GLS", group="sex")
fit.4 <- cfa(fit.model, data=HolzingerSwineford1939, estimator="GLD", group="sex", group.equal="regressions") 
anova(fit, fit.4)

Output

The output consists of three sections.

The first section (first 6 lines) contains the package version number, an indication whether the model has converged (and in how many iterations), and the effective number of observations used in the analysis.

The second section contains the model χ^2 test statistic, degrees of freedom, and a p value are printed. If fit.measures = TRUE, it also prints the test statistic of the baseline model (where all observed variables are assumed to be uncorrelated) and several popular fit indices. If maximum likelihood estimation is used, this section will also contain information about the log-likelihood, the AIC, and the BIC.

The third section provides an overview of the parameter estimates, including the type of standard errors used and whether the observed or expected information matrix was used to compute standard errors. Then, for each model parameter, the estimate and the standard error are displayed, and if appropriate, a z value based on the Wald test and a corresponding two-sided p value are also shown. To ease the reading of the parameter estimates, they are grouped into three blocks:

factor loadings,

factor covariances, and

residual variances of both observed variables and factors.

The summary() method provides a nice summary of the model results for visualization purposes. The parameterEstimates() method returns the actual parameter estimates as a data.frame, which can be processed further.

parameterEstimates(fit)

Index	lhs	op	rhs	est	se	z	pvalue	ci.lower	ci.upper
1	visual	=~	x1	1	0	NA	NA	1	1
2	visual	=~	x2	0.553	0.1	5.554	0	0.358	0.749
3	visual	=~	x3	0.729	0.109	6.685	0	0.516	0.943
4	textual	=~	x4	1	0	NA	NA	1	1
5	textual	=~	x5	1.113	0.065	17.014	0	0.985	1.241
6	textual	=~	x6	0.926	0.055	16.703	0	0.817	1.035
7	speed	=~	x7	1	0	NA	NA	1	1
8	speed	=~	x8	1.18	0.165	7.152	0	0.857	1.503
9	speed	=~	x9	1.082	0.151	7.155	0	0.785	1.378
10	x1	~~	x1	0.549	0.114	4.833	0	0.326	0.772
11	x2	~~	x2	1.134	0.102	11.146	0	0.934	1.333
12	x3	~~	x3	0.844	0.091	9.317	0	0.667	1.022
13	x4	~~	x4	0.371	0.048	7.779	0	0.278	0.465
14	x5	~~	x5	0.446	0.058	7.642	0	0.332	0.561
15	x6	~~	x6	0.356	0.043	8.277	0	0.272	0.441
16	x7	~~	x7	0.799	0.081	9.823	0	0.64	0.959
17	x8	~~	x8	0.488	0.074	6.573	0	0.342	0.633
18	x9	~~	x9	0.566	0.071	8.003	0	0.427	0.705
19	visual	~~	visual	0.809	0.145	5.564	0	0.524	1.094
20	textual	~~	textual	0.979	0.112	8.737	0	0.76	1.199
21	speed	~~	speed	0.384	0.086	4.451	0	0.215	0.553
22	visual	~~	textual	0.408	0.074	5.552	0	0.264	0.552
23	visual	~~	speed	0.262	0.056	4.66	0	0.152	0.373
24	textual	~~	speed	0.173	0.049	3.518	0	0.077	0.27

The confidence level can be changed by setting the level argument. To obtain several standardized versions of the estimates, we can use standardized = TRUE:

est <- parameterEstimates(fit, ci = FALSE, standardized = TRUE)

subset(est, op == "=~")

Index	lhs	op	rhs	est	se	z	pvalue	std.lv	std.all	std.nox
1	visual	=~	x1	1	0	NA	NA	0.9	0.772	0.772
2	visual	=~	x2	0.553	0.1	5.554	0	0.498	0.424	0.424
3	visual	=~	x3	0.729	0.109	6.685	0	0.656	0.581	0.581
4	textual	=~	x4	1	0	NA	NA	0.99	0.852	0.852
5	textual	=~	x5	1.113	0.065	17.014	0	1.102	0.855	0.855
6	textual	=~	x6	0.926	0.055	16.703	0	0.917	0.838	0.838
7	speed	=~	x7	1	0	NA	NA	0.619	0.57	0.57
8	speed	=~	x8	1.18	0.165	7.152	0	0.731	0.723	0.723
9	speed	=~	x9	1.082	0.151	7.155	0	0.67	0.665	0.665

This only shows the factor loadings are shown but 3 additional columns with standardized values are added.

In the first column (std.lv), only the latent variables have been standardized;

In the second column (std.all), both the latent and the observed variables have been standardized;

In the third column (std.nox), both the latent and the observed variables have been standardized, except for the exogenous observed variables. This option may be useful if the standardization of exogenous observed variables has little meaning (for example, binary covariates). Since there are no exogenous covariates in this model, the last two columns are identical in this output.

library("semPlot")
# semPaths(fit, "std", "show")
semPaths(fit, "std", curvePivot = TRUE, edge.label.cex = 1.0) 
# get the margines right:
# semPaths(fit, "std", curvePivot = TRUE, edge.label.cex = 1.0, mar = c(10, 3, 10, 3)) 
# semPaths(fit, "std", curvePivot = TRUE, edge.label.cex = 1.0, mar = c(10, 3, 10, 3), as.expression = c("nodes", 
# 	"edges"), sizeMan = 3, sizeInt = 1, sizeLat = 4)

See also

• Back to Structural Equation Modeling (SEM)
• Next Section: SEM Example 2: Parkinson’s Disease data

---

• SOCR Home page: http://www.socr.umich.edu

---

---

Translate this page:

(default)	Deutsch	Español	Français	Italiano	Português	日本語	България	الامارات العربية المتحدة	Suomi	इस भाषा में	Norge
한국어	中文	繁体中文	Русский	Nederlands	Ελληνικά	Hrvatska	Česká republika	Danmark	Polska	România	Sverige