Difference between revisions of "AP Statistics Curriculum 2007 Prob Rules"
| Line 5: | Line 5: | ||
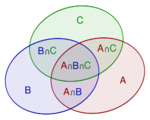
[[Image:500px-Inclusion-exclusion.svg.png|150px|thumbnail|right| [http://upload.wikimedia.org/wikipedia/commons/thumb/4/42/Inclusion-exclusion.svg/180px-Inclusion-exclusion.svg.png Venn Diagrams]]] | [[Image:500px-Inclusion-exclusion.svg.png|150px|thumbnail|right| [http://upload.wikimedia.org/wikipedia/commons/thumb/4/42/Inclusion-exclusion.svg/180px-Inclusion-exclusion.svg.png Venn Diagrams]]] | ||
| + | For events ''A''<sub>1</sub>, ..., ''A''<sub>''n''</sub> in a probability space (S,P), the probability of the union for ''n=2'' is | ||
| + | :<math>\mathbb{P}(A_1\cup A_2)=\mathbb{P}(A_1)+\mathbb{P}(A_2)-\mathbb{P}(A_1\cap A_2),</math> | ||
| + | |||
| + | For ''n=3'', | ||
| + | |||
| + | :<math>\begin{align}\mathbb{P}(A_1\cup A_2\cup A_3)&=\mathbb{P}(A_1)+\mathbb{P}(A_2)+\mathbb{P}(A_3)\\ | ||
| + | &\qquad-\mathbb{P}(A_1\cap A_2)-\mathbb{P}(A_1\cap A_3)-\mathbb{P}(A_2\cap A_3)+\mathbb{P}(A_1\cap A_2\cap A_3) | ||
| + | \end{align}</math> | ||
| + | |||
| + | In general, for any ''n'', | ||
| + | |||
| + | :<math>\begin{align} | ||
| + | \mathbb{P}\biggl(\bigcup_{i=1}^n A_i\biggr) & {} =\sum_{i=1}^n \mathbb{P}(A_i) | ||
| + | -\sum_{i,j\,:\,i<j}\mathbb{P}(A_i\cap A_j) \\ | ||
| + | &\qquad+\sum_{i,j,k\,:\,i<j<k}\mathbb{P}(A_i\cap A_j\cap A_k)-\ \cdots\cdots\ \pm \mathbb{P}\biggl(\bigcap_{i=1}^n A_i\biggr), | ||
| + | \end{align}</math> | ||
| + | |||
| + | This can also be written in closed form as | ||
| + | |||
| + | :<math>\mathbb{P}\biggl(\bigcup_{i=1}^n A_i\biggr) =\sum_{k=1}^n (-1)^{k-1}\sum_{\scriptstyle I\subset\{1,\ldots,n\}\atop\scriptstyle|I|=k} \mathbb{P}\biggl(\bigcap_{i\in I} A_i\biggr),</math> | ||
| + | |||
| + | where the last sum runs over all subsets ''I'' of the indices 1, ..., ''n'' which contain exactly ''k'' elements. | ||
=== Multiplication Rule=== | === Multiplication Rule=== | ||
Revision as of 22:56, 28 January 2008
Contents
General Advance-Placement (AP) Statistics Curriculum - Probability Theory Rules
Addition Rule
The probability of a union, also called the Inclusion-Exclusion principle allows us to compute probabilities of composite events represented as unions (i.e., sums) of simpler events.
For events A1, ..., An in a probability space (S,P), the probability of the union for n=2 is
\[\mathbb{P}(A_1\cup A_2)=\mathbb{P}(A_1)+\mathbb{P}(A_2)-\mathbb{P}(A_1\cap A_2),\]
For n=3,
\[\begin{align}\mathbb{P}(A_1\cup A_2\cup A_3)&=\mathbb{P}(A_1)+\mathbb{P}(A_2)+\mathbb{P}(A_3)\\ &\qquad-\mathbb{P}(A_1\cap A_2)-\mathbb{P}(A_1\cap A_3)-\mathbb{P}(A_2\cap A_3)+\mathbb{P}(A_1\cap A_2\cap A_3) \end{align}\]
In general, for any n,
\[\begin{align} \mathbb{P}\biggl(\bigcup_{i=1}^n A_i\biggr) & {} =\sum_{i=1}^n \mathbb{P}(A_i) -\sum_{i,j\,:\,i<j}\mathbb{P}(A_i\cap A_j) \\ &\qquad+\sum_{i,j,k\,:\,i<j<k}\mathbb{P}(A_i\cap A_j\cap A_k)-\ \cdots\cdots\ \pm \mathbb{P}\biggl(\bigcap_{i=1}^n A_i\biggr), \end{align}\]
This can also be written in closed form as
\[\mathbb{P}\biggl(\bigcup_{i=1}^n A_i\biggr) =\sum_{k=1}^n (-1)^{k-1}\sum_{\scriptstyle I\subset\{1,\ldots,n\}\atop\scriptstyle|I|=k} \mathbb{P}\biggl(\bigcap_{i\in I} A_i\biggr),\]
where the last sum runs over all subsets I of the indices 1, ..., n which contain exactly k elements.
Multiplication Rule
Model Validation
Checking/affirming underlying assumptions.
- TBD
Computational Resources: Internet-based SOCR Tools
- TBD
Examples
Computer simulations and real observed data.
- TBD
Hands-on activities
Step-by-step practice problems.
- TBD
References
- TBD
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: