Difference between revisions of "EBook Problems MultivariateNormal"
(→EBook Problems Set - Mutivariate Normal Distribution) |
(→EBook Problems Set - Mutivariate Normal Distribution) |
||
| Line 379: | Line 379: | ||
Therefore, extending the channel capacity to about <math>104.5</math> <math>m^3/sec</math> will cut the risk by half. | Therefore, extending the channel capacity to about <math>104.5</math> <math>m^3/sec</math> will cut the risk by half. | ||
}} | }} | ||
| + | |||
| + | ===Problem 5=== | ||
| + | Fibers may be embedded in cement to increase its strength. Consider a cracked section as shown in the following diagram: | ||
| + | |||
| + | [[Image:Problem 5.jpg|250x250px|center]] | ||
| + | |||
| + | Suppose the total strength T of the cracked section is given by the following expression: | ||
| + | |||
| + | <math> | ||
| + | T=C+(F_1+F_2+...+F_N) | ||
| + | </math> | ||
| + | |||
| + | Where C is the strength contributed by the cement; <math>F_1</math>, <math>F_2</math>, etc. are the strength of each of the fibers across the crack; N is the total number of fibers across the crack. Suppose C=N(30,5); each <math>F_i</math> is N(5,3) and N is a discrete random variable with the following PMF | ||
| + | |||
| + | |||
| + | [[Image:Problem 5 PMF.jpg|600x600px|center]] | ||
| + | |||
| + | Assume C and <math>F_i</math>'s are statistically independent. What is the probability that the total strength T will be less than 30? | ||
| + | |||
| + | ===Problem 6=== | ||
| + | [[Image:Problem 6.jpg|300x300px|center]] | ||
| + | |||
| + | The settlement of each footing shown follows a normal distribution with a mean of 2 inches and a coefficient of variation of 30%. Suppose the settlements between two adjacent footings are correlated with a correlation coefficient of 0.7. suppose | ||
| + | |||
| + | <math>D=S_1-S_2</math> | ||
| + | |||
| + | where <math>S_1</math> and <math>S_2</math> are settlements of footings 1 and 2, respectively. | ||
| + | |||
| + | ''(a) Determine the mean and variance of D. | ||
| + | |||
| + | ''(b) What is the probability that the magnitude of the differential settlement (i.e., the difference between the settlements of two adjacent footings) will be less than 0.5 inch? | ||
Revision as of 23:30, 22 January 2011
Contents
[hide]EBook Problems Set - Mutivariate Normal Distribution
Problem 1
Person1 and Person2 are travelling from point A to point D, but there are different routes to get from A to D. Person1 decides to take the A->B->D route, whereas Person2 takes the A->C->D route.
The travel times (in hours) between each pair of points indicated are normally distributed as follows:
T1 ~ N (6, 2)
T2 ~ N (4, 1)
T3 ~ N (5, 3)
T4 ~ N (4, 1)
Explain why these times are stochastic (and not exact or deterministic)? Although the travel times here generally can be assumed statistically independent, T3 and T4 are dependent with correlation coefficient 0.8.
(a) What is the probability that Person2 will not arrive at point D within 10 hours?
(b) What is the probability that Person1 will arrive at point D earlier than Person2 by at least one hour?
(c) Which route (A\(\rightarrow\)B\(\rightarrow\)D or A\(\rightarrow\)C\(\rightarrow\)D) should be taken if one wishes to minimize the expected travel time from A to D? Explain.
{\sigma_{T2}}\leq\frac{10-9}{3.847076812})
=1-\Phi(0.259937622)=1-0.602543999
\cong 0.397 \) }}
) \, \)
Hence
\( =\Phi (-0.44946657) \, \)
\( \cong 0.327 \, \) }}
Problem 2
The settlement (in cm) of a structure shown in the following figure may be evaluated from
\( S=0.3A+0.2B+0.1C \)
where A, B, and C are respectively the thickness (in m) of the three layers of soil as shown. Suppose A, B, and C are modeled as independent normal random variables as
A ~ N(5,1)
B ~ N(8,2)
C ~ N(7,1)
(a) Determine the probability that the settlement will exceed 4 cm.
(b) If the total thickness of the three layers is known exactly as 20 m; and furthermore, thicknesses A and B are correlated with correlation coefficient equal to 0.5, determine the probability that the settlement will exceed 4 cm.
) \, \)
\( =1-\Phi(0.57735027)=1-0.718148613 \cong 0.282 \, \) }}
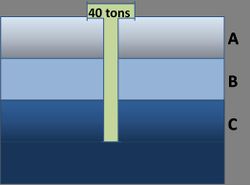
Problem 3
A friction pile is driven through three soil layers as shown in the following figure:
The total bearing capacity of the friction pile (in tons) is obtained from
\( Q=4A+B+2C \)
Where A, B, and C are penetration lengths (in meters) through each of the three soil layers, respectively. Suppose A ~ N(5,3); B ~ N(8,2); A and B are negatively correlated with coefficient \(\rho\) = - 0.5. The total length of the pile is 30 meters. Determine the probability that the pile will fail to support the 40 ton load, i.e., the event that the capacity Q is less than 40 tons. [Hint: Observe C = 30 - (A+B)].
) \, \)
\( =\Phi(-3.050851079) \, \)
\( \cong0.00114 \, \) }}
Problem 4
A city is located at the downstream of the confluence point of two rivers as shown. The annual maximum flood peak in River 1 has an average of \(35 m^2/sec\) with the standard deviation of \(10 m^3/sec\), whereas in River 2 the mean peak flow rate is \(25 m^3/sec\) and the standard deviation is \(10 m^3/sec\). The annual maximum peak flow rates in both rivers are normally distributed with a correlation coefficient of 0.5. Presently, the channel which runs through the city can accommodate up to \(100 m^3/sec\) flow rate without flooding the city. Please answer the following questions.
(a) What are the mean and standard deviation of the annual maximum peak discharge passing through the city?
(b) What is the annual risk that the city will experience flooding based on the existing channel capacity? What is the corresponding return period?
(c) Calculate the probability that the city will experience flooding over a 10-year period.
(d) If the desired flooding risk over a 10 year period is to be reduced by half, how large should the present channel capacity be extended to?
)=p \)
\( \Rightarrow 1-\Phi(\frac{X_0-60}{\sqrt{300}})=0.005106623 \)
\( \Rightarrow \Phi((\frac{X_0-60}{\sqrt{300}}))=0.994893377 \)
\( \Rightarrow X_0=60+\Phi^{-1}(0.994893377)\sqrt{300} \)
\( =60+2.568522177 \sqrt{300} = 104.4881091 \)
Therefore, extending the channel capacity to about \(104.5\) \(m^3/sec\) will cut the risk by half. }}
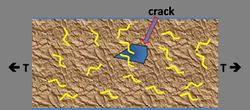
Problem 5
Fibers may be embedded in cement to increase its strength. Consider a cracked section as shown in the following diagram:
Suppose the total strength T of the cracked section is given by the following expression\[ T=C+(F_1+F_2+...+F_N) \]
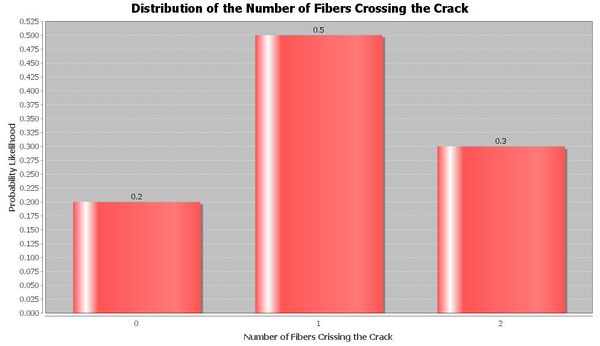
Where C is the strength contributed by the cement; \(F_1\), \(F_2\), etc. are the strength of each of the fibers across the crack; N is the total number of fibers across the crack. Suppose C=N(30,5); each \(F_i\) is N(5,3) and N is a discrete random variable with the following PMF
Assume C and \(F_i\)'s are statistically independent. What is the probability that the total strength T will be less than 30?
Problem 6
The settlement of each footing shown follows a normal distribution with a mean of 2 inches and a coefficient of variation of 30%. Suppose the settlements between two adjacent footings are correlated with a correlation coefficient of 0.7. suppose
\(D=S_1-S_2\)
where \(S_1\) and \(S_2\) are settlements of footings 1 and 2, respectively.
(a) Determine the mean and variance of D.
(b) What is the probability that the magnitude of the differential settlement (i.e., the difference between the settlements of two adjacent footings) will be less than 0.5 inch?
- Back to Ebook
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: