AP Statistics Curriculum 2007 Gamma

Gamma Distribution

Definition: Gamma distribution is a distribution that arises naturally in processes for which the waiting times between events are relevant. It can be thought of as a waiting time between Poisson distributed events.

Probability density function: The waiting time until the hth Poisson event with a rate of change \(\lambda\) is

\[P(x)=\frac{\lambda(\lambda x)^{h-1}}{(h-1)!}{e^{-\lambda x}}\]

For \(X\sim \operatorname{Gamma}(k,\theta)\!\), where \(k=h\) and \(\theta=1/\lambda\), the gamma probability density function is given by

\[\frac{x^{k-1}e^{-x/\theta}}{\Gamma(k)\theta^k}\]

where

• e is the natural number (e = 2.71828…)
• k is the number of occurrences of an event
• if k is a positive integer, then \(\Gamma(k)=(k-1)!\) is the gamma function
• \(\theta=1/\lambda\) is the mean number of events per time unit, where \(\lambda\) is the mean time between events. For example, if the mean time between phone calls is 2 hours, then you would use a gamma distribution with \(\theta\)=1/2=0.5. If we want to find the mean number of calls in 5 hours, it would be 5 \(\times\) 1/2=2.5.
• x is a random variable

Cumulative density function: The gamma cumulative distribution function is given by

\[\frac{\gamma(k,x/\theta)}{\Gamma(k)}\]

where

• if k is a positive integer, then \(\Gamma(k)=(k-1)!\) is the gamma function
• \(\textstyle\gamma(k,x/\theta)=\int_0^{x/\theta}t^{k-1}e^{-t}dt\)

Moment generating function: The gamma moment-generating function is

\[M(t)=(1-\theta t)^{-k}\!\]

Expectation: The expected value of a gamma distributed random variable x is

\[E(X)=k\theta\!\]

Variance: The gamma variance is

\[Var(X)=k\theta^2\!\]

Applications

The gamma distribution can be used a range of disciplines including queuing models, climatology, and financial services. Examples of events that may be modeled by gamma distribution include:

• The amount of rainfall accumulated in a reservoir
• The size of loan defaults or aggregate insurance claims
• The flow of items through manufacturing and distribution processes
• The load on web servers
• The many and varied forms of telecom exchange

The gamma distribution is also used to model errors in a multi-level Poisson regression model because the combination of a Poisson distribution and a gamma distribution is a negative binomial distribution.

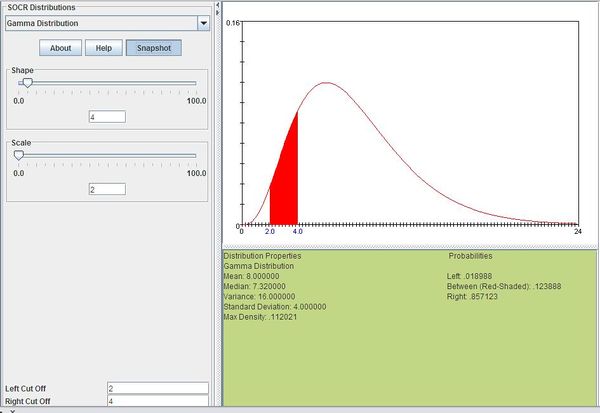
Example

Suppose you are fishing and you expect to get a fish once every 1/2 hour. Compute the probability that you will have to wait between 2 to 4 hours before you catch 4 fish.

One fish every 1/2 hour means we would expect to get \(\theta=1 / 0.5=2\) fish every hour on average. Using \(\theta=2\) and \(k=4\), we can compute this as follows:

\[P(2\le X\le 4)=\sum_{x=2}^4\frac{x^{4-1}e^{-x/2}}{\Gamma(4)2^4}=0.12388\]

The figure below shows this result using SOCR distributions