Difference between revisions of "SMHS ROC"
(→Applications) |
|||
| Line 35: | Line 35: | ||
|rowspan=2| ||rowspan=2| ||colspan=2|Disease Status||colspan=2|Metrics | |rowspan=2| ||rowspan=2| ||colspan=2|Disease Status||colspan=2|Metrics | ||
|- | |- | ||
| − | |Disease||No Disease||Prevalence= | + | |Disease||No Disease||Prevalence=$\frac{\sum Condition\, positive}{\sum Total\, population}$ || |
|- | |- | ||
| − | |rowspan=2|Screening Test||Positive||a (True positives)||b (False positives)||Positive predictive value (PPV)= | + | |rowspan=2|Screening Test||Positive||a (True positives)||b (False positives)||Positive predictive value (PPV)=$\frac{\sum Ture\, positive}{\sum Test\,positives}$||False discovery rate (FDR)==$\frac{\sum False\, positive}{\sum Test\, positive}$ |
|- | |- | ||
| − | |Negative||c (False negatives)||d (True negatives)||False omission rate (FOR)= | + | |Negative||c (False negatives)||d (True negatives)||False omission rate (FOR)=$\frac{\sum False\, negative} {\sum Test\, negative}$||Negative predictive value (NPV)=$\frac{\sum True\, negative}{\sum Test\, negative}$ |
|- | |- | ||
| − | | ||Positive Likelihood Ratio=TPR/FBR||True positive rate (TPR)= | + | | ||Positive Likelihood Ratio=TPR/FBR||True positive rate (TPR)=$\frac{\sum True\, positive} {\sum Condition\, positive}$||False positive rate (FPR)=$\frac{\sum False\, positive}{\sum Condition\, positive}$||Accuracy(ACC)=$\frac{\sum True\, positive}+ {\sum True\, negative} {\sum Total\, population}$| || |
|- | |- | ||
| − | | ||Negative Likelihood Ratio=FNR/TNR||False negative rate (FNR)= | + | | ||Negative Likelihood Ratio=FNR/TNR||False negative rate (FNR)=$\frac{\sum False\, negative} {\sum condition\, negative}$||True negative rate (TNR)=$\frac{\sum True\, negative}{\sum Condition\, negative}$||True negative rate (TNR)=$\frac\sum True\, negative}{\sum Condition\, negative}$| || |
|} | |} | ||
</center> | </center> | ||
| Line 146: | Line 146: | ||
</center> | </center> | ||
| − | Plot sensitivity vs. specificity, we have the ROC curve: | + | Plot sensitivity vs. specificity, we have the ROC curve: |
| − | + | x<-c(0,0.01,0.19,0.58,1) | |
| − | x<-c(0,0.01,0.19,0.58,1) | + | y<-c(0,0.56,0.78,0.91,1) |
| − | + | plot(x,y,type='o',main='ROC curve for T4',xlab='False positive rate (specificity)',ylab='True positive rate (sensitivity)') | |
| − | y<-c(0,0.56,0.78,0.91,1) | ||
| − | |||
| − | plot(x,y,type='o',main='ROC curve for T4',xlab='False positive rate (specificity)',ylab='True positive rate (sensitivity)') | ||
<center> | <center> | ||
[[File:ROC Fig 1.png]] | [[File:ROC Fig 1.png]] | ||
Revision as of 15:24, 28 August 2014
Contents
Scientific Methods for Health Sciences - Receiver Operating Characteristic (ROC) Curve
Overview
Receiver operating characteristic (ROC curve) is a graphical plot, which illustrates the performance of a binary classifier system as its discrimination threshold varies. The ROC curve is created by plotting the fraction of true positive out of the total actual positives vs. the fraction of false positives out of the total actual negatives at various threshold settings. In this section, we are going to introduce the ROC curve and illustrate applications of this method with examples.
Motivation
We have talked about the cases with a binary classification where the outcomes are either absent or present and the test results are positive or negative. We have also discussed about sensitivity and specificity of a test and are familiar with the concepts of true positive and true negatives. With ROC curve, we are looking to demonstrate the following aspects:
- To show the tradeoff between sensitivity and specificity;
- The closer the curve follows the left-hand border and top border of ROC space, the more accurate is the test;
- The closer the curve comes to the 45-degree diagonal, the less accurate is the test;
- The slope of the tangent line at a cut-point gives the likelihood ratio for the value of the test;
- The area under the curve is a measure of text accuracy.
| Actual condition | |||
| Absent (H_0 is true) | Present (H_1 is true) | ||
| Test Result | Negative (fail to reject H_0) | Condition absent + Negative result = True (accurate) Negative (TN, 0.98505) | Condition present + Negative result = False (invalid) Negative (FN, 0.00025)Type II error (β) |
| Positive | (reject H_0) Condition absent + Positive result = False Positive (FP, 0.00995) Type I error (α) | Condition Present + Positive result = True Positive (TP, 0.00475) | |
| Test Interpretation | Power = 1-FN=1-0.00025 = 0.99975 | Specificity: TN/(TN+FP) =0.98505/(0.98505+0.00995) = 0.99 | Sensitivity: TP/(TP+FN) =0.00475/(0.00475+ 0.00025)= 0.95 |
Theory
Review of basic concepts in a binary classification:
| Disease Status | Metrics | ||||
| Disease | No Disease | Prevalence=$\frac{\sum Condition\, positive}{\sum Total\, population}$ | |||
| Screening Test | Positive | a (True positives) | b (False positives) | Positive predictive value (PPV)=$\frac{\sum Ture\, positive}{\sum Test\,positives}$ | False discovery rate (FDR)==$\frac{\sum False\, positive}{\sum Test\, positive}$ |
| Negative | c (False negatives) | d (True negatives) | False omission rate (FOR)=$\frac{\sum False\, negative} {\sum Test\, negative}$ | Negative predictive value (NPV)=$\frac{\sum True\, negative}{\sum Test\, negative}$ | |
| Positive Likelihood Ratio=TPR/FBR | True positive rate (TPR)=$\frac{\sum True\, positive} {\sum Condition\, positive}$ | False positive rate (FPR)=$\frac{\sum False\, positive}{\sum Condition\, positive}$ | |||
| Negative Likelihood Ratio=FNR/TNR | False negative rate (FNR)=$\frac{\sum False\, negative} {\sum condition\, negative}$ | True negative rate (TNR)=$\frac{\sum True\, negative}{\sum Condition\, negative}$ | |||
Introduction of ROC Curve:
Sensitivity and specificity are both characteristics of a test but they also depend on the definition of what constitutes an abnormal test. Consider a medical test on diagnostic tests where the cut-points would without doubt influence the test results. We can use the hypothyroidism data from the likelihood ratio to illustrate how these two characteristics change depending on the choice of T4 level that defines hypothyroidism. Recall the data where patients with suspected hypothyroidism are reported.
| T4 | <1 | 1-2 | 2-3 | 3-4 | 4-5 | 5-6 | 6-7 | 7-8 | 8-9 | 9-10 | 10-11 | 11-12 | >12 |
| Hypothyroid | 2 | 3 | 1 | 8 | 4 | 4 | 3 | 3 | 1 | 0 | 2 | 1 | 0 |
| Euthyroid | 0 | 0 | 0 | 0 | 1 | 6 | 11 | 19 | 17 | 20 | 11 | 4 | 4 |
With the following cut-points, we have the data listed:
| T4 value | Hypothyroid | Euthyroid |
| 5 or less | 18 | 1 |
| 5.1 - 7 | 7 | 17 |
| 7.1 - 9 | 4 | 36 |
| 9 or more | 3 | 39 |
| Totals: | 32 | 93 |
Suppose that patients with T4 of 5 or less are considered to be hypothyroid, then the data would be displayed as the following and the sensitivity is 0.56 and specificity is 0.99 in this case.
| T4 value | Hypothyroid | Euthyroid |
| 5 or less | 18 | 1 |
| More than 5 | 14 | 92 |
| Totals: | 32 | 93 |
Now suppose, we decided to be less stringent on the disease and consider the patients with T4 values of 7 or less to be hypothyroid, then the data would be recorded as the following and the sensitivity in this case would be 0.78 and specificity 0.81:
| T4 value | Hypothyroid | Euthyroid |
| 7 or less | 25 | 18 |
| More than 7 | 7 | 75 |
| Totals: | 32 | 93 |
If we move the cut-point for hypothyroidism a little bit higher, say 9, we would have the sensitivity of 0.91 and specificity 0.42:
| T4 value | Hypothyroid | Euthyroid |
| 9 or less | 29 | 54 |
| More than 9 | 3 | 39 |
| Totals: | 32 | 93 |
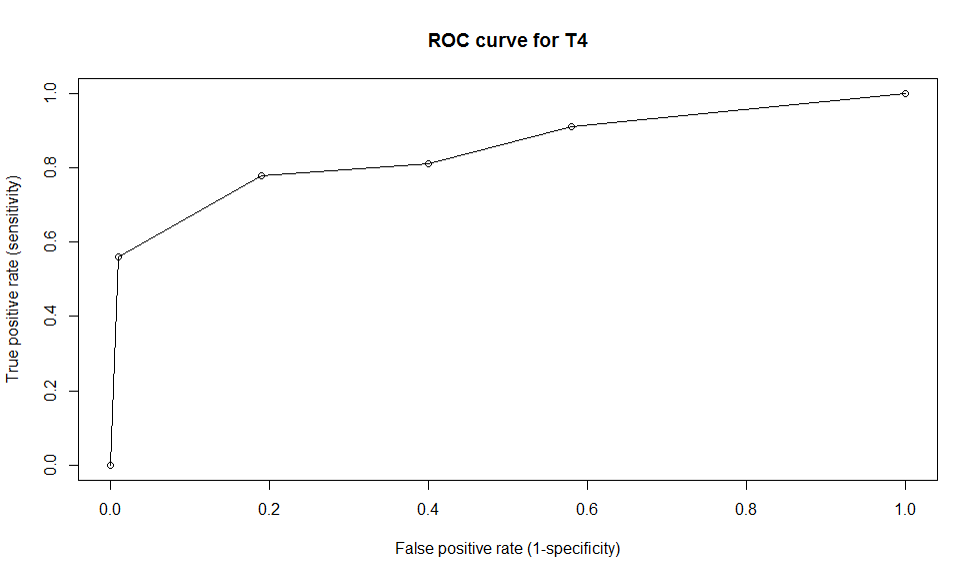
To sum up, we have the pairs of sensitivity an specificity with corresponding cut-points in the following table:
| Cut points | Sensitivity | Specificity |
| 5 | 0.56 | 0.99 |
| 7 | 0.78 | 0.81 |
| 9 | 0.91 | 0.42 |
From the table above, we observe that the sensitivity improves with increasing cut-point T4 value while specificity increases with decreasing cut-point T4 value. That is a tradeoff between sensitivity and specificity. The table above can also be shown as TP and FP.
| Cut points | True positives | False positives |
| 5 | 0.56 | 0.01 |
| 7 | 0.78 | 0.19 |
| 9 | 0.91 | 0.58 |
Plot sensitivity vs. specificity, we have the ROC curve: x<-c(0,0.01,0.19,0.58,1) y<-c(0,0.56,0.78,0.91,1) plot(x,y,type='o',main='ROC curve for T4',xlab='False positive rate (specificity)',ylab='True positive rate (sensitivity)')
- Accuracy of a test is measured by the area under the ROC Curve and a rough guide for classifying the accuracy of a diagnostic test is traditional academic point system: 0.90-1:excellent;0.8-0.9: good (B);0.7-0.8:fair (C);0.6-0.7:poor (D);0.5-0.7:fail (F).
With our example above, the area under the T4 ROC curve is 0.86, which shows that the accuracy of the test is good in separating hypothyroid from euthyroid patients.
- How to calculate the area under the curve? The area measures discrimination, which is the ability of the test to correctly classify those with and without the disease. The area under the curve is the percentage of randomly drawn pairs for which this is true. Two methods are commonly used to calculate the area of the scope: (1) non-parametric method based on constructing trapezoids under the curve as approximation of area; (2) a parametric method using a MLE to fit a smooth curve to data points.
Applications
This article titled The Meaning And the Use Of The Area Under A Receiver Operating Characteristic (ROC) Curve presented a representation and interpretation of the area under a ROC curve obtained by the ‘rating’ method, or by mathematical predictions based on patient characteristics. It showed that that in such a setting the area represents the probability that a randomly chosen diseased subject is (correctly) rated or ranked with greater suspicion than a randomly chosen non-diseased subject.
This article illustrated practical experimental techniques for measuring ROC curves and discussed about the issues of case selection and curve-fitting. It also talked about possible generalizations of conventional ROC analysis to account for decision performance in complex diagnostic tasks and showed ROC analysis related in direct and natural way to cost/benefit analysis of diagnostic decision making. This paper developed the concepts of ‘average diagnostic cost’ and ‘average net benefit’ to identify the optimal compromise among various kinds of diagnostic error and suggested ways in ROC analysis to optimize diagnostic strategies.
Software
# With the given example in R: x<-c(0,0.01,0.19,0.58,1) y<-c(0,0.56,0.78,0.91,1) plot(x,y,type='o',main='ROC curve for T4',xlab='False positive rate (specificity)',ylab='True positive rate (sensitivity)')
Problems
6.1) Suppose that a new study is conducted on lung cancer and the following data is collected in identify between two types of lung cancers (say type a and type b). Conduct the ROC curve for this example by varying the cut-points from 2 to 10 by increasing 2 units each time. Calculate the area under the curve and interpret on the accuracy of the test.
| measurements | <1 | 1-2 | 2-3 | 3-4 | 4-5 | 5-6 | 6-7 | 7-8 | 8-9 | 9-10 | 10-11 | 11-12 | >12 |
| Type a | 2 | 1 | 4 | 2 | 8 | 7 | 4 | 3 | 0 | 0 | 1 | 2 | 2 |
| Type b | 1 | 3 | 0 | 2 | 2 | 5 | 10 | 23 | 18 | 20 | 15 | 8 | 2 |
6.2) When a serious disease can be treated if it is caught early, it is more important to have a test with high specificity than high sensitivity.
a. True
b. False
6.3) The positive predictive value of a test is calculated by dividing the number of:
(a) True positives in the population
(b) True negatives in the population
(c) People who test positive
(d) People who test negative
6.4) A new screening test has been developed for diabetes. The table below represents the results of the new test compared to the current gold standard.
| Condition positive | Condition negative | Total | |
| Test positive | 80 | 70 | 150 |
| Test negative | 10 | 240 | 250 |
| Total | 90 | 310 | 400 |
What is the sensitivity of the test?
(a) 77%
(b) 89%
(c) 80%
(d) 53%
6.5) What is the specificity of the test?
(a) 77%
(b) 89%
(c) 80%
(d) 53%
6.6) What is the positive predictive value of the test?
(a) 77%
(b) 89%
(c) 80%
(d) 53%
7) References
Statistical inference / George Casella, Roger L. Berger. http://mirlyn.lib.umich.edu/Record/004199238
Sampling / Steven K. Thompson. http://mirlyn.lib.umich.edu/Record/004232056
Sampling theory and methods / S. Sampath. http://mirlyn.lib.umich.edu/Record/004133572
Introduction to ROC Curves http://gim.unmc.edu/dxtests/roc1.htm