Difference between revisions of "SMHS MethodsHeterogeneity"
(Created page with "== Scientific Methods for Health Sciences - Methods for Studying Heterogeneity of Treatment Effects, Case-Studies of Comparative Effectiveness Research ==") |
|||
| Line 1: | Line 1: | ||
==[[SMHS| Scientific Methods for Health Sciences]] - Methods for Studying Heterogeneity of Treatment Effects, Case-Studies of Comparative Effectiveness Research == | ==[[SMHS| Scientific Methods for Health Sciences]] - Methods for Studying Heterogeneity of Treatment Effects, Case-Studies of Comparative Effectiveness Research == | ||
| + | |||
| + | <center>[[Image:SMHS_Methods1.png|500px]] </center> | ||
| + | |||
| + | Adopted from: http://dx.doi.org/10.1186/1471-2288-12-185 | ||
| + | |||
| + | * *CART: Classification and regression tree (CART) analysis | ||
| + | * ** LGM/GMM: Latent growth modeling/Growth mixture modeling. | ||
| + | * *** QTE: Quantile Treatment Effect. | ||
| + | * **** Standard meta-analysis like fixed and random effect models, and tests of heterogeneity, together with various plots and summaries, can be found in the R-package <bn>rmeta</b> (http://cran.r-project.org/web/packages/rmeta). Non-parametric R approaches are included in the <b>np</b> package, http://cran.r-project.org/web/packages/np/vignettes/np.pdf. | ||
| + | |||
| + | <b>Methods Summaries</b> | ||
| + | |||
| + | <b>Overview</b> | ||
| + | |||
| + | Recursive partitioning is a data mining technique for exploring structure and patterns in complex data. It facilitates the visualization of decision rules for predicting categorical (classification tree) or continuous (regression tree) outcome variables. The R <b>rpart</b> package provides the tools for Classification and Regression Tree (CART) modeling, conditional inference trees, and random forests. Additional resources include an Introduction to Recursive Partitioning Using the RPART Routines . The <b>Appendix</b> includes description of the main CART analysis steps. | ||
| + | |||
| + | <b>install.packages("rpart")</b> | ||
| + | <b>library("rpart")</b> | ||
| + | |||
| + | I. <b><u>CART</u></b> (Classification and Regression Tree) is a decision-tree based technique that considers how variation observed in a given response variable (continuous or categorical) can be understood through a systematic deconstruction of the overall study population into subgroups, using explanatory variables of interest. For HTE analysis, CART is best suited for early-stage, exploratory analyses. Its relative simplicity can be powerful in identifying basic relationships between variables of interest, and thus identify potential subgroups for more advanced analyses. The key to CART is its ‘systematic’ approach to the development of the subgroups, which are constructed sequentially through repeated, binary splits of the population of interest, one explanatory variable at a time. In other words, each ‘parent’ group is divided into two ‘child’ groups, with the objective of creating increasingly homogeneous subgroups. The process is repeated and the subgroups are then further split, until no additional variables are available for further subgroup development. The resulting tree structure is oftentimes overgrown, but additional techniques are used to ‘trim’ the tree to a point at which its predictive power is balanced against issues of over-fitting. Because the CART approach does not make assumptions regarding the distribution of the dependent variable, it can be used in situations where other multivariate modeling techniques often used for exploratory predictive risk modeling would not be appropriate – namely in situations where data are not normally distributed. | ||
| + | |||
| + | CART analyses are useful in situations where there is some evidence to suggest that HTE exists, but the subgroups defining the heterogeneous response are not well understood. CART allows for an exploration of response in a myriad of complex subpopulations, and more recently developed ensemble methods (such as Bayesian Additive Regression Trees) allow for more robust analyses through the combination of multiple CART analyses. | ||
| + | |||
| + | <b>Example Fifth Dutch growth study</b> | ||
| + | |||
| + | # Let’s use the Fifth Dutch growth study (2009) <b>fdgs</b> . Is it true that “the world’s tallest nation has stopped growing taller: the height of Dutch children from 1955 to 2009”? | ||
| + | |||
| + | #install.packages("mice") | ||
| + | library("mice") | ||
| + | ?fdgs | ||
| + | head(fdgs) | ||
Revision as of 12:47, 7 March 2016
Scientific Methods for Health Sciences - Methods for Studying Heterogeneity of Treatment Effects, Case-Studies of Comparative Effectiveness Research
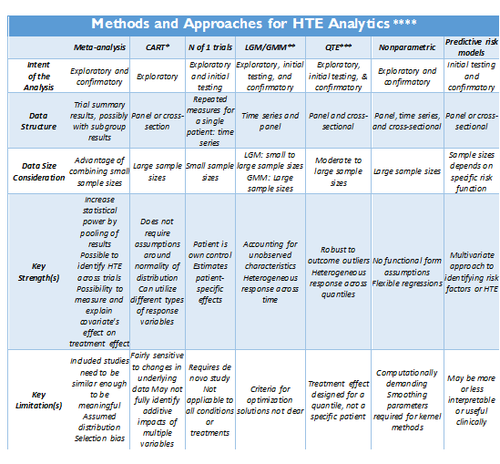
Adopted from: http://dx.doi.org/10.1186/1471-2288-12-185
- *CART: Classification and regression tree (CART) analysis
- ** LGM/GMM: Latent growth modeling/Growth mixture modeling.
- *** QTE: Quantile Treatment Effect.
- **** Standard meta-analysis like fixed and random effect models, and tests of heterogeneity, together with various plots and summaries, can be found in the R-package <bn>rmeta (http://cran.r-project.org/web/packages/rmeta). Non-parametric R approaches are included in the np package, http://cran.r-project.org/web/packages/np/vignettes/np.pdf.
Methods Summaries
Overview
Recursive partitioning is a data mining technique for exploring structure and patterns in complex data. It facilitates the visualization of decision rules for predicting categorical (classification tree) or continuous (regression tree) outcome variables. The R rpart package provides the tools for Classification and Regression Tree (CART) modeling, conditional inference trees, and random forests. Additional resources include an Introduction to Recursive Partitioning Using the RPART Routines . The Appendix includes description of the main CART analysis steps.
install.packages("rpart")
library("rpart")
I. CART (Classification and Regression Tree) is a decision-tree based technique that considers how variation observed in a given response variable (continuous or categorical) can be understood through a systematic deconstruction of the overall study population into subgroups, using explanatory variables of interest. For HTE analysis, CART is best suited for early-stage, exploratory analyses. Its relative simplicity can be powerful in identifying basic relationships between variables of interest, and thus identify potential subgroups for more advanced analyses. The key to CART is its ‘systematic’ approach to the development of the subgroups, which are constructed sequentially through repeated, binary splits of the population of interest, one explanatory variable at a time. In other words, each ‘parent’ group is divided into two ‘child’ groups, with the objective of creating increasingly homogeneous subgroups. The process is repeated and the subgroups are then further split, until no additional variables are available for further subgroup development. The resulting tree structure is oftentimes overgrown, but additional techniques are used to ‘trim’ the tree to a point at which its predictive power is balanced against issues of over-fitting. Because the CART approach does not make assumptions regarding the distribution of the dependent variable, it can be used in situations where other multivariate modeling techniques often used for exploratory predictive risk modeling would not be appropriate – namely in situations where data are not normally distributed.
CART analyses are useful in situations where there is some evidence to suggest that HTE exists, but the subgroups defining the heterogeneous response are not well understood. CART allows for an exploration of response in a myriad of complex subpopulations, and more recently developed ensemble methods (such as Bayesian Additive Regression Trees) allow for more robust analyses through the combination of multiple CART analyses.
Example Fifth Dutch growth study
# Let’s use the Fifth Dutch growth study (2009) fdgs . Is it true that “the world’s tallest nation has stopped growing taller: the height of Dutch children from 1955 to 2009”?
#install.packages("mice")
library("mice")
?fdgs
head(fdgs)