SOCR EduMaterials Activities Discrete Probability examples

• Description: You can access the applets for the distributions at http://www.socr.ucla.edu/htmls/SOCR_Distributions.html .
• Example 1:

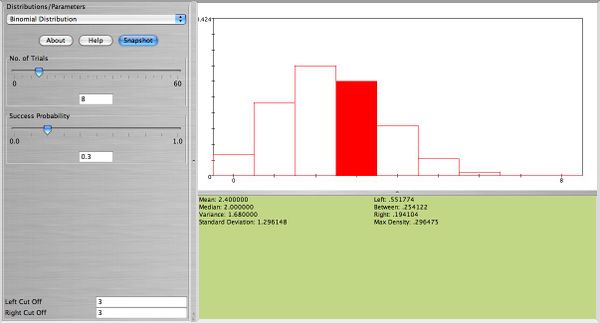
Find the probability that 3 out of 8 plants will survive a frost, given that any such plant will survive a frost with probability of 0.30. Also, find the probability that at least 1 out of 8 will survive a frost. What is the expected value and standard deviation of the number of plants that survive the frost?

• Answer:
• \( X \sim b(8,0.3) \), \( P(X=3)= {8 \choose 3} 0.3^30.7^5=0.2541\)
• \( P(X \ge 1)=1-P(X=0)=1-.7^8=0.942\)
• \( E(X) = np = 8 \times 0.3=2.4 \)
• \( Sd(X)= \sqrt{npq}=\sqrt{8\times 0.30 \times 0.70}=1.3\)

Below you can see a SOCR snapshot for this example:

• Example 2:

If the probabilities of having a male or female offspring are both 0.50, find the probability that a familiy's fifth child is their first son.

• Answer:
• \(P(X=5)= 0.50^5=0.03125\)
• Example 3:
  • a. \(X \sim b(4,0.8) \), \( P(X=2)= {4 \choose 2} 0.8^2 0.2^2=0.1536\)
  • b. \(P(X\ge 2)= {4 \choose 2} 0.8^2 0.2^2+{4 \choose 3} 0.8^3 0.2^1+{4 \choose 4} 0.8^4=0.9728\)
• Example 4:
• \(0.7^4 0.3=0.07203\)
• Example 5:

\( X \sim g(\frac{1}{0.30} \)

• Example 6:
  • a. \(X \sim b(5,0.90) \), \( P(X=4)= {5 \choose 4} 0.9^4 0.1^1\)
  • \(P(X\ge 1)= 1-P(X=0)= 1- 0.1^4 \)
  • b. \(P(X=0)= 1-0.999= .001\)

\(0.001= 0.1^n\) \(n= 3\)