Difference between revisions of "SOCR EduMaterials Activities BirthdayExperiment"
(→Exact Calculations) |
|||
| Line 48: | Line 48: | ||
Denote by ''P(E)'' the probability of the [[AP_Statistics_Curriculum_2007_Prob_Basics#Event_Manipulations|complementary event]], E = {All ''N'' birthdays are ''different''}. Then, | Denote by ''P(E)'' the probability of the [[AP_Statistics_Curriculum_2007_Prob_Basics#Event_Manipulations|complementary event]], E = {All ''N'' birthdays are ''different''}. Then, | ||
| − | :<math>P(E) = 1 \times \left(1-\frac{1}{365}\right) \times \left(1-\frac{2}{365}\right) \cdots \left(1-\frac{N-1}{365}\right) = { 365 \times 364 \cdots (365-N+1) \over 365^N } = { 365! \over 365^N (365-N)!}</math> | + | :<math>P(E) = 1 \times \left(1-\frac{1}{365}\right) \times \left(1-\frac{2}{365}\right) \times\cdots \times\left(1-\frac{N-1}{365}\right)</math> |
| + | : <math>P(E) = { 365 \times 364\times \cdots \times(365-N+1) \over 365^N } = { 365! \over 365^N (365-N)!}</math> | ||
because the second person cannot have the same birthday as the first one, <math>\left(1-\frac{1}{365}\right)=\frac{364}{365}</math>, the third cannot have the same birthday as the first two, <math>\left(1-\frac{2}{365}\right)=\frac{363}{365}</math>, the forth cannot have the same birthday as the first three, <math>\left(1-\frac{3}{365}\right)=\frac{362}{365}</math>, etc. | because the second person cannot have the same birthday as the first one, <math>\left(1-\frac{1}{365}\right)=\frac{364}{365}</math>, the third cannot have the same birthday as the first two, <math>\left(1-\frac{2}{365}\right)=\frac{363}{365}</math>, the forth cannot have the same birthday as the first three, <math>\left(1-\frac{3}{365}\right)=\frac{362}{365}</math>, etc. | ||
Revision as of 12:35, 2 April 2008
Contents
The Birthday Experiment
Description
From a population of size m, individual balls are numbered 1 to m. A random sample of size n with replacement is drawn during every run. V is the random variables of interest which represent the number of distinct values in the sample, and I represents the indicator variable that specifies at least one duplicate in the sample. In the data table below, the values of V and I are recorded after every trial. Above the data table are the sampled balls in which red symbolizes a duplicate ball within the trial and green as balls that have not been previously chosen. On the upper right is a graph that illustrates the probability density function in blue and the empirical density function in red. The numerical values are recorded in the distribution table. Parameters m and n can be modified to the experimenter’s discretion by using the scroll bars. Note: interested if a match has occurred (I=1)
Goal
The purpose of this experiment is to draw attention toward the behaviors of random sampling with replacement.
Experiment
Go to the SOCR Experiments and select the Birthday Experiment from the drop-down list of experiments on the top left. The image below shows the initial view of this experiment:

When pressing the play button, one trial will be executed and recorded in the distribution table below. The fast forward button symbolizes the nth number of trials to be executed each time. The stop button ceases any activity and is helpful when the experimenter chooses “continuous,” indicating an infinite number of events. The fourth button will reset the entire experiment, deleting all previous information and data collected. The “update” scroll indicates nth number of trials (1, 10, 100, or 1000) performed when selecting the fast forward button and the “stop” scroll indicates the maximum number of trials in the experiment.
When data is drawn according to I, as value of m increases, the probability density function graph for 1 decreases and the probability density function graph of 0 increases. As the value of n increases, the probability density graph for 1 increases and the probability density graph for 0 decreases.

When variable V is the chosen element of interest, the probability density function is skewed left when m is large. Modifying n changes the spread of the graph—a large value of n gives small values on the y-axis and large distribution on x-axis while a small value of n gives large values on the y-axis and small distribution on x-axis.
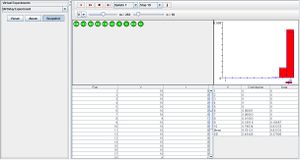
As the number of trials increase, the empirical density function graph in red begins to look more similar to the probability density graph in blue.
Applications
The Birthday Experiment may be used for many different types of events that involve selecting individual elements from a large population. Setting variable V as the desired event in the Birthday Experiment may represent a quality (e.g. birth date, age, height, etc.) for every person in a city and variable I as two distinct variables that are being represented (e.g. gender, left/right-handed, married/single, etc.). Note that the probability density graph could be symbolized as a hypothesis in this experiment.
For example, researchers are interested to know the probability of selecting a male who is born on May 15, 1986.
The Birthday Paradox
The Birthday Paradox is not a real paradox, despite the fact that its statement may initially sound a little counter-intuitive. Suppose we have a random group of N people. What is the change that at least two people have the same birthday? For example, if N=20, P(one-or-more-Birthday-matches) > 0.4. Main confusion arises from the fact that in real life we rarely meet people having the same birthday as us, and we meet more than 20 people.
The reason for such a high probability is that any of the 20 people can compare their birthday with any other one, not just you comparing your birthday to anybody else’s.
Approximate Argument
There are \({N \choose 2} = 20*19/2=190\) ways to select a pair or people from a pool of 20 people. Assume there are 365 days in a year, P(one-particular-pair-same-B-day)=1/365, and P(one-particular-pair-failure)=1-1/365 ~ 0.99726. For N=20, let the event E={No 2 people have the same birthday}. Then E is the event {all 190 pairs fail (i.e., have different birthdays)}, then (assuming independence of each of these individual events!) \(P(E) = P(failure)^{190} = 0.99726^{190} = 0.59\). Hence, P(at-least-one-success)=1-0.59=0.41, quite high. Note: for N=42, P > 0.9.
Exact Calculations
Denote by P(E) the probability of the complementary event, E = {All N birthdays are different}. Then,
\[P(E) = 1 \times \left(1-\frac{1}{365}\right) \times \left(1-\frac{2}{365}\right) \times\cdots \times\left(1-\frac{N-1}{365}\right)\] \[P(E) = { 365 \times 364\times \cdots \times(365-N+1) \over 365^N } = { 365! \over 365^N (365-N)!}\]
because the second person cannot have the same birthday as the first one, \(\left(1-\frac{1}{365}\right)=\frac{364}{365}\), the third cannot have the same birthday as the first two, \(\left(1-\frac{2}{365}\right)=\frac{363}{365}\), the forth cannot have the same birthday as the first three, \(\left(1-\frac{3}{365}\right)=\frac{362}{365}\), etc.
The event of at least two of the N people having the same birthday is complementary to E, i.e., we are interested in the probability \(P(E^c)\), which is equal to
\[ P(E^c) = 1 - P(E).\]
For N = 23, \(P(E^c) \approx 0.507\), and for N = 100, \(P(E^c) \approx 0.9999996\). You can explicitely compute all these probabilities for any N using the Birthday Experiment in SOCR Experiments.
Translate this page: