Difference between revisions of "SOCR EduMaterials Activities ApplicationsActivities StockSimulation"
(New page: == A Model for Stock prices == * '''Description''': You can access the stock simulation applet at http://www.socr.ucla.edu/htmls/app/ . * Process for Stock Prices: Assumed a drift rate...) |
|||
| Line 29: | Line 29: | ||
\frac{\Delta S}{S}=0.14 \Delta t + 0.20 \epsilon \sqrt{\Delta t} | \frac{\Delta S}{S}=0.14 \Delta t + 0.20 \epsilon \sqrt{\Delta t} | ||
</math> | </math> | ||
| − | * Find the distribution of the change in <math>S<math> divided by <math>S<math> at the end of the first year. That is, find the distribution of <math>\frac{\Delta S}{S}</math>. <br> | + | * Find the distribution of the change in <math>S</math> divided by <math>S</math> at the end of the first year. That is, find the distribution of <math>\frac{\Delta S}{S}</math>. <br> |
<math> | <math> | ||
\frac{\Delta S}{S} \sim N\left(0.10 \Delta t, 0.20 \sqrt{\Delta t}\right). | \frac{\Delta S}{S} \sim N\left(0.10 \Delta t, 0.20 \sqrt{\Delta t}\right). | ||
| Line 56: | Line 56: | ||
\Delta S_1 = S_0 + \Delta S_1 = 20 + 0.26=20.26. | \Delta S_1 = S_0 + \Delta S_1 = 20 + 0.26=20.26. | ||
</math> | </math> | ||
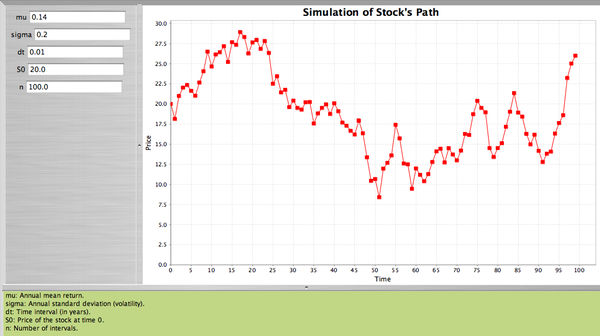
| − | We continue in the same fashion until we reach the end of the year. | + | We continue in the same fashion until we reach the end of the year. Here is the SOCR applet. |
<center>[[Image: Christou_stock_simulation.jpg|600px]]</center> | <center>[[Image: Christou_stock_simulation.jpg|600px]]</center> | ||
Revision as of 11:14, 3 August 2008
A Model for Stock prices
- Description: You can access the stock simulation applet at http://www.socr.ucla.edu/htmls/app/ .
- Process for Stock Prices: Assumed a drift rate equal to \(\mu S\) where \(\mu\) is the expected return of the stock, and variance \(\sigma^2 S^2\) where \(\sigma^2\) is the variance of the return of the stock. From Weiner process the model for stock prices is\[ \Delta S = \mu S \Delta t + \sigma S \epsilon \sqrt{\Delta t} \]
or
\(
\frac{\Delta S}{S} = \mu \Delta t + \sigma \epsilon \sqrt{\Delta t}.
\)
Therefore
\(
\frac{\Delta S}{S} \sim N(\mu \Delta t, \sigma \sqrt{\Delta t}).
\)
\(S\) Price of the stock.
\(\Delta S\) Change in the stock price.
\(\Delta t\) Small interval of time.
\(\epsilon\) Follows \(N(0,1)\).
- Example: The current price of a stock is \(S_0=\$100\). The expected return is \(\mu=0.10\) per year, and the standard deviation of the return is \(\sigma=0.20\) (also per year).
- Find an expression for the process of the stock.
\( \frac{\Delta S}{S}=0.14 \Delta t + 0.20 \epsilon \sqrt{\Delta t} \)
- Find the distribution of the change in \(S\) divided by \(S\) at the end of the first year. That is, find the distribution of \(\frac{\Delta S}{S}\).
\( \frac{\Delta S}{S} \sim N\left(0.10 \Delta t, 0.20 \sqrt{\Delta t}\right). \)
- Divide the year in weekly intervals and find the distribution of \(\frac{\Delta S}{S}\) at the end of each weekly interval.
\(
\frac{\Delta S}{S} \sim N\left(0.10 \frac{1}{52}, 0.20 \sqrt{\frac{1}{52}}\right).
\)
- Therefore, sampling from this distribution we can simulate the path of the stock. The price of the stock at the end of the first interval will be \(S_1 = S_0 + \Delta S_1\), where \(\Delta S_1\) is the change during the first time interval, etc.
- Using the SOCR applet we will simulate the stock's path by dividing one year into small intervals each one of length \(\frac{1}{100}\) of a year, when \(S_0=\$20<math>, annual mean and standard deviation'"`UNIQ-MathJax2-QINU`"'.
<br>
* The applet will select a random sample of 100 observations from <math>N(0,1)\) and will compute
\(
\frac{\Delta S}{S} = 0.14 (0.01) + 0.20 \epsilon \sqrt{0.01}.
\)
Suppose that \(\epsilon_1=0.58\). Then
\(
\frac{\Delta S}{S} = 0.14 (0.01) + 0.20 (0.58) \sqrt{0.01}= 0.013 \Rightarrow \Delta S_1= 20(0.013)=0.26.
\)
Therefore
\(
\Delta S_1 = S_0 + \Delta S_1 = 20 + 0.26=20.26.
\)
We continue in the same fashion until we reach the end of the year. Here is the SOCR applet.