AP Statistics Curriculum 2007 Prob Rules
Contents
General Advance-Placement (AP) Statistics Curriculum - Probability Theory Rules
Addition Rule
The probability of a union, also called the Inclusion-Exclusion principle allows us to compute probabilities of composite events represented as unions (i.e., sums) of simpler events.
For events A1, ..., An in a probability space (S,P), the probability of the union for n=2 is \[P(A_1\cup A_2)=P(A_1)+P(A_2)-P(A_1\cap A_2),\]
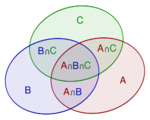
For n=3, \[P(A_1\cup A_2\cup A_3)=P(A_1)+P(A_2)+P(A_3) -P(A_1\cap A_2)-P(A_1\cap A_3)-P(A_2\cap A_3)+P(A_1\cap A_2\cap A_3)\]
In general, for any n, \[P(\bigcup_{i=1}^n A_i) =\sum_{i=1}^n P(A_i) -\sum_{i,j\,:\,i<j}P(A_i\cap A_j) +\sum_{i,j,k\,:\,i<j<k}P(A_i\cap A_j\cap A_k)+ \cdots\cdots\ +(-1)^{j+1} P(\bigcap_{i=1}^j A_i)+ \cdots\cdots\ +(-1)^{n+1} P(\bigcap_{i=1}^n A_i).\]
Conditional Probability
The conditional probability of A occurring given that B occurs is given by \[P(A | B) ={P(A \cap B) \over P(B)}.\]
Multiplication Rule
Model Validation
Checking/affirming underlying assumptions.
- TBD
Computational Resources: Internet-based SOCR Tools
- TBD
Examples
Computer simulations and real observed data.
- TBD
Hands-on activities
Step-by-step practice problems.
- TBD
References
- TBD
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: