SOCR EduMaterials Activities ApplicationsActivities StockSimulation
A Model for Stock prices
Description
You can access the portfolio applet at the SOCR Applications Site, select Financial Applications --> StockSimulation.
- Process for Stock Prices: Assumed a drift rate equal to \(\mu S\) where \(\mu\) is the expected return of the stock, and variance \(\sigma^2 S^2\) where \(\sigma^2\) is the variance of the return of the stock. From Weiner process the model for stock prices is:
\[ \Delta S = \mu S \Delta t + \sigma S \epsilon \sqrt{\Delta t}
\]
or
\[
\frac{\Delta S}{S} = \mu \Delta t + \sigma \epsilon \sqrt{\Delta t}.
\]
Therefore
\[
\frac{\Delta S}{S} \sim N(\mu \Delta t, \sigma \sqrt{\Delta t}).
\]
\[S\] Price of the stock.
\[\Delta S\] Change in the stock price.
\[\Delta t\] Small interval of time.
\[\epsilon\] Follows \(N(0,1)\).
Example
The current price of a stock is \(S_0=\$100\). The expected return is \(\mu=0.10\) per year, and the standard deviation of the return is \(\sigma=0.20\) (also per year).
- Find an expression for the process of the stock.
\( \frac{\Delta S}{S}=0.14 \Delta t + 0.20 \epsilon \sqrt{\Delta t} \)
- Find the distribution of the change in \(S\) divided by \(S\) at the end of the first year. That is, find the distribution of \(\frac{\Delta S}{S}\).
\[ \frac{\Delta S}{S} \sim N\left(0.10 \Delta t, 0.20 \sqrt{\Delta t}\right). \]
- Divide the year in weekly intervals and find the distribution of \(\frac{\Delta S}{S}\) at the end of each weekly interval.
\[
\frac{\Delta S}{S} \sim N\left(0.10 \frac{1}{52}, 0.20 \sqrt{\frac{1}{52}}\right).
\]
- Therefore, sampling from this distribution we can simulate the path of the stock. The price of the stock at the end of the first interval will be \(S_1 = S_0 + \Delta S_1\), where \(\Delta S_1\) is the change during the first time interval, etc.
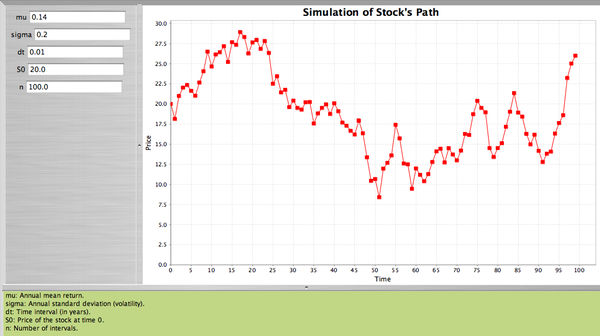
- Using the SOCR applet we will simulate the stock's path by dividing one year into small intervals each one of length \(\frac{1}{100}\) of a year, when \(S_0=\$20\), annual mean and standard deviation\[\mu=0.14, \sigma=0.20\].
- The applet will select a random sample of 100 observations from \(N(0,1)\) and will compute
\[ \frac{\Delta S}{S} = 0.14 (0.01) + 0.20 \epsilon \sqrt{0.01}.
\]
Suppose that \(\epsilon_1=0.58\). Then
\[ \frac{\Delta S}{S} = 0.14 (0.01) + 0.20 (0.58) \sqrt{0.01}= 0.013 \Rightarrow \Delta S_1= 20(0.013)=0.26. \]
Therefore
\[ \Delta S_1 = S_0 + \Delta S_1 = 20 + 0.26=20.26. \]
We continue in the same fashion until we reach the end of the year. Here is the SOCR applet.
- The materials above was partially taken from
Modern Portfolio Theory by Edwin J. Elton, Martin J. Gruber, Stephen J. Brown, and William N. Goetzmann, Sixth Edition, Wiley, 2003, and Options, Futues, and Other Derivatives by John C. Hull, Sixth Edition, Pearson Prentice Hall, 2006.
Translate this page: