UQuadraticDistribuionAbout
Contents
About_pages_for_SOCR_Distributions - U-Quadratic Distribution
Description
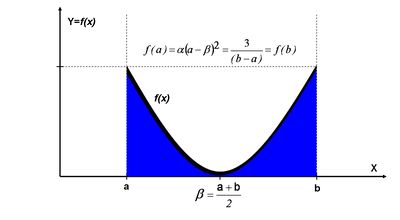
The U quadratic distribution is defined by the following density function
where the relation between the two pairs of parameters (domain-support, a and b) and (range/offset \(\alpha\) and \(\beta\)) are given by the following two equations
More information about U-quadratic, and other continuous distribution functions, is available at Wikipedia.
Properties
- Support Parameters\[a < b \in (-\infty,\infty)\]
- Scale/Offset Parameters\[\alpha \in (0,\infty)\] and \(\beta \in (-\infty,\infty)\)
- PDF\[f(x)=\alpha \left ( x - \beta \right )^2, \forall x \in [a , b]\]
- CDF \(F(x)={\alpha \over 3} \left ( (x - \beta)^3 + (\beta - a)^3 \right ), \forall x \in [a , b]\)
- Mean\[{a+b \over 2}\]
- Median\[{a+b \over 2}\]
- Modes\[a \] and \( b \)
- Variance\[ {3 \over 20} (b-a)^2 \]
- Skewness: 0 (distribution is symmetric around the mean)
- Kurtosis\[ {3 \over 112} (b-a)^4 \]
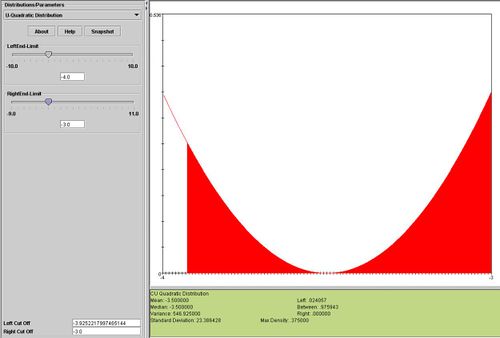
Interactive U Quadratic Distribution
You can see the interactive U Quadratic distribution by going to SOCR Distributions and selecting from the drop down list of distributions U Quadratic. Then follow the Help instructions to dynamically set parameters, compute critical and probability values using the mouse and keyboard.
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: