SOCR EduMaterials Activities Discrete Probability examples
- Description: You can access the applets for the distributions at http://www.socr.ucla.edu/htmls/SOCR_Distributions.html .
- Example 1:
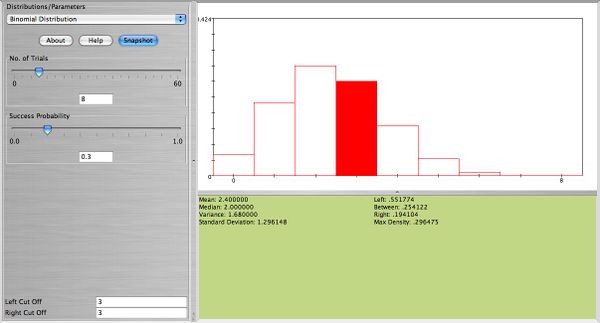
Find the probability that 3 out of 8 plants will survive a frost, given that any such plant will survive a frost with probability of 0.30. Also, find the probability that at least 1 out of 8 will survive a frost. What is the expected value and standard deviation of the number of plants that survive the frost?
- Answer:
- \( X \sim b(8,0.3) \), \( P(X=3)= {8 \choose 3} 0.3^30.7^5=0.2541\)
- \( P(X \ge 1)=1-P(X=0)=1-.7^8=0.942\)
- \( E(X) = np = 8 \times 0.3=2.4 \)
- \( Sd(X)= \sqrt{npq}=\sqrt{8\times 0.30 \times 0.70}=1.3\)
Below you can see SOCR snapshots for this example:

- Example 2:
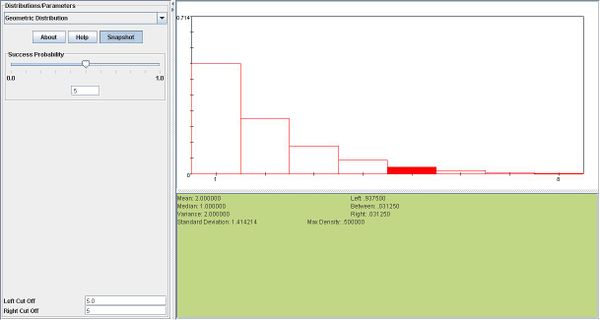
If the probabilities of having a male or female offspring are both 0.50, find the probability that a familiy's fifth child is their first son.
- Answer:
- \(P(X=5)= 0.50^5=0.03125\)
- Example 3:
- a. \(X \sim b(4,0.8) \), \( P(X=2)= {4 \choose 2} 0.8^2 0.2^2=0.1536\)
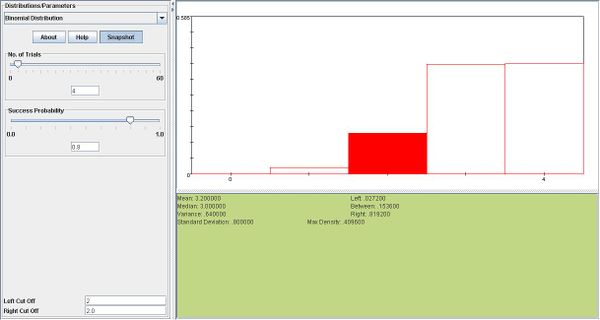
- b. \(P(X\ge 2)= {4 \choose 2} 0.8^2 0.2^2+{4 \choose 3} 0.8^3 0.2^1+{4 \choose 4} 0.8^4=0.9728\)

- Example 4:
- \(P(X=5)=0.7^4 0.3=0.07203\) where X represents the number of trials.

- Example 5:
\( E(X)=\frac{1}{p}=\frac{1}{0.30}=3.33\)
- Example 6:
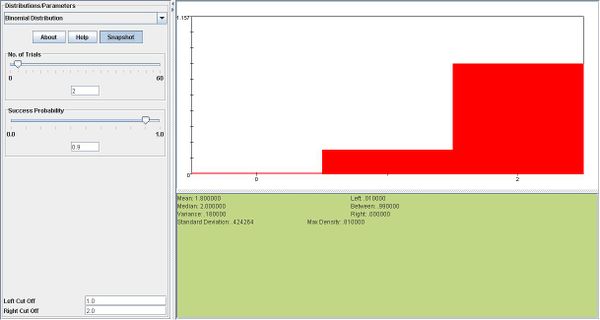
- a. \(X \sim b(5,0.90). P(X=4)= {5 \choose 4} 0.9^4 0.1^1=0.32805\)

- \(P(X\ge 1)= 1-P(X=0)= 1- 0.1^4=0.9999\)

- b. \(P(X=0)=.001, 0.001= 0.1^n n= 3.\)
- In the first snapshot below, where\(n=2, P(X\ge1)=0.99,\) which is too small. In the second snapshot, we can see that when n is increased to 3, \(P(X\ge1)\) increases to nearly 1.

- Example 7:
Construct a probability histogram for the binomial probability distribution for each of the following: n=5,p=0.1, n=5,p=0.5, m=5,n=0.9. What do you observe? Explain.
- Answer:
We observe that if p=0.5 the distribution resembles the normal distribution, with mean \(np=0.25\). Values above and below the mean are distributed symmetrically around the mean. Also, the probability histograms for p=0.1 and p=0.9 are mirror images of each other.

- Example 8:
On a population of consumers, 60% prefer a certain brand of ice cream. If consumers are randomly selected,
- a. what is the probability that exactly 3 people have to be interviewed to encounter the first consumer who prefers this brand of ice cream?
- b. what is the probability that at least 3 people have to be interviewed to encounter the first consumer who prefers this brand of ice cream?
- Answer:
- a. \(P(X=3)=P(The first consumer does not prefer this new brand) \times P(The second consumer does not prefer this new brand) \times P(The third consumer does prefer this new brand)= 0.4 \times 0.4 \times 0.6=0.096\)
- b. Let's first find the probability that at least 3 people will NOT have to be interviewed to encounter the first case.
\(P(X=1) + P(X=2) = 0.6+0.4 \times 0.6 = 0.84\)
- Now we subtract this from 1 to find the complement\[1-0.84= 0.16\]
- Example 9: