SOCR EduMaterials Activities Discrete Probability examples

• Description: You can access the applets for the distributions at http://www.socr.ucla.edu/htmls/SOCR_Distributions.html .
• Example 1:

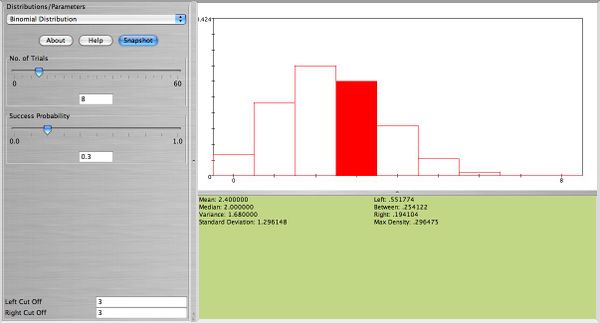
Find the probability that 3 out of 8 plants will survive a frost, given that any such plant will survive a frost with probability of 0.30. Also, find the probability that at least 1 out of 8 will survive a frost. What is the expected value and standard deviation of the number of plants that survive the frost?

• Answer:
• \( X \sim b(8,0.3) \), \( P(X=3)= {8 \choose 3} 0.3^30.7^5=0.2541\)
• \( P(X \ge 1)=1-P(X=0)=1-.7^8=0.942\)
• \( E(X) = np = 8 \times 0.3=2.4 \)
• \( Sd(X)= \sqrt{npq}=\sqrt{8\times 0.30 \times 0.70}=1.3\)

Below you can see SOCR snapshots for this example:

• Example 2:

If the probabilities of having a male or female offspring are both 0.50, find the probability that a familiy's fifth child is their first son.

• Answer:
• \(P(X=5)= 0.50^5=0.03125\)

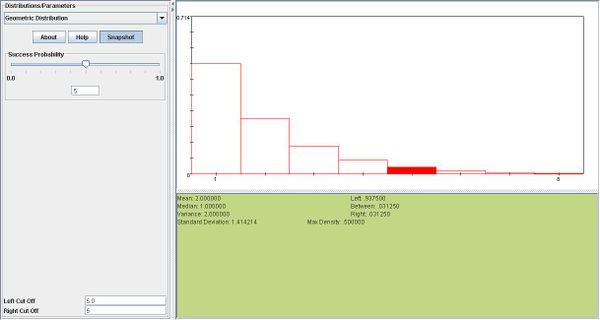
• Example 3:

A complex electronic system is built with a certain number of backup components in its subsystem. One subsystem has 4 identical components, each with probability of 0.20 of failing in less than 1000 hours. The subsystem will operate if at least 2 of the 4 components are operating. Assume the components operate independently.

• Answer:
  • a. Find the probability that exactly 2 of the 4 components last longer than 1000 hours.
  • b. Find the probability that the subsystem operates longer than 1000 hours.
  • a. \(X \sim b(4,0.8) \), \( P(X=2)= {4 \choose 2} 0.8^2 0.2^2=0.1536\)

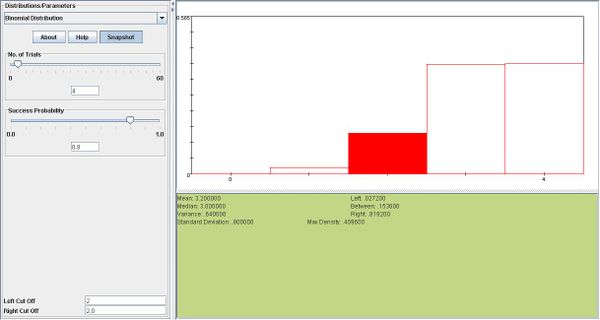
• • b. \(P(X\ge 2)= {4 \choose 2} 0.8^2 0.2^2+{4 \choose 3} 0.8^3 0.2^1+{4 \choose 4} 0.8^4=0.9728\)

• Example 4:
• \(P(X=5)=0.7^4 0.3=0.07203\) where X represents the number of trials.

• Example 5:

\( E(X)=\frac{1}{p}=\frac{1}{0.30}=3.33\)

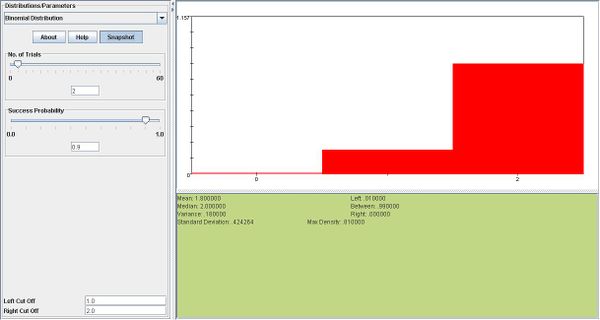
• Example 6:
  • a. \(X \sim b(5,0.90). P(X=4)= {5 \choose 4} 0.9^4 0.1^1=0.32805\)

• • \(P(X\ge 1)= 1-P(X=0)= 1- 0.1^4=0.9999\)

• • b. \(P(X=0)=.001, 0.001= 0.1^n n= 3.\)
• In the first snapshot below, where\(n=2, P(X\ge1)=0.99,\) which is too small. In the second snapshot, we can see that when n is increased to 3, \(P(X\ge1)\) increases to nearly 1.

• Example 7:

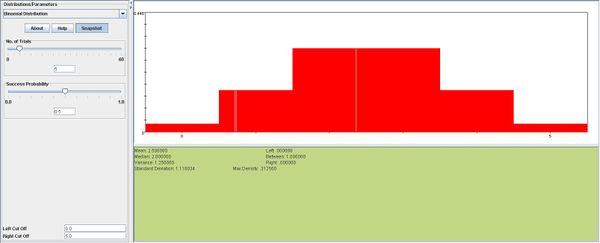
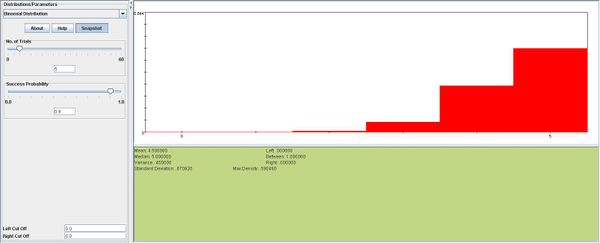
Construct a probability histogram for the binomial probability distribution for each of the following: n=5,p=0.1, n=5,p=0.5, m=5,n=0.9. What do you observe? Explain.

• Answer:

We observe that if p=0.5 the distribution resembles the normal distribution, with mean \(np=0.25\). Values above and below the mean are distributed symmetrically around the mean. Also, the probability histograms for p=0.1 and p=0.9 are mirror images of each other.

• Example 8:

On a population of consumers, 60% prefer a certain brand of ice cream. If consumers are randomly selected,

• • a. what is the probability that exactly 3 people have to be interviewed to encounter the first consumer who prefers this brand of ice cream?

• • b. what is the probability that at least 3 people have to be interviewed to encounter the first consumer who prefers this brand of ice cream?

• Answer:
  • a. \(P(X=3)=0.4 \times 0.4 \times 0.6=0.096\)
  • b. Let's first find the probability that at least 3 people will NOT have to be interviewed to encounter the first case.

\(P(X=1) + P(X=2) = 0.6+0.4 \times 0.6 = 0.84\)

• Now we subtract this from 1 to find the complement, which is the event that at least 3 people WILL have to be interviewed to find the first case\[1-0.84= 0.16\]

• Example 9:

The alpha marketing research company employs consumer panels to explore preferences

• Answer:
  • a. \( X \sim b(5,0.4) \), \( P(X=5)= {5 \choose 5} 0.4^5 0.6^0=0.01024\)

• • b. In this part we will look at every group of 5 people as one unit. We will denote success as the event that all 5 people in a group prefer the new product, and failure as the event that at least one person in a group does not prefer the new product. Therefore, \(p=0.01024\). So,

\(P(X=60)= (1-.01024)^60 = 53.9%\)

• Below you can see a SOCR snapshot for this example:

• Example 10:
• Answer:
• a. We will denote the number of unbruised peaches in our first selection X, and the number of unbruised peaches in our second selection Y. \(P(shipment=A)=\)P(all four peaches are unbruised)+P(three of the peaches are unbruised) X P(four additional peaches are unbruised)=\(P(X=4)+P(X=3)\times P(Y=4). *<math> X \sim b(4,0.9) \), \( P(X=4)= {4 \choose 4} 0.9^4 0.1^0= 0.6561\)
• \( Y \sim b(4,0.9) \), \( P(X=3)= {4 \choose 3} 0.9^3 0.1^1= 0.6561\)
• \( Y \sim b(4,0.9) \), \( P(X=4)= {4 \choose 4} 0.9^4 0.1^0= 0.6561\)