SOCR EduMaterials Activities Discrete Probability examples

• Description: You can access the applets for the distributions at http://www.socr.ucla.edu/htmls/SOCR_Distributions.html .
• Example 1:

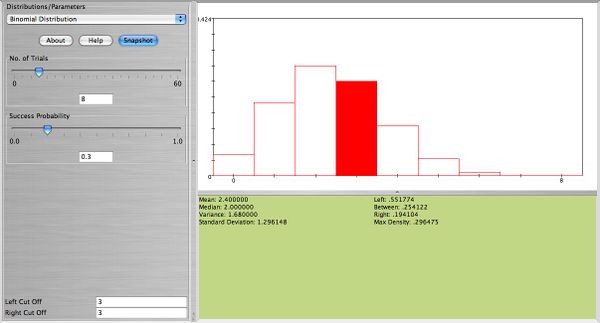
Find the probability that 3 out of 8 plants will survive a frost, given that any such plant will survive a frost with probability of 0.30. Also, find the probability that at least 1 out of 8 will survive a frost. What is the expected value and standard deviation of the number of plants that survive the frost?

• Answer:
• \( X \sim b(8,0.3) \), \( P(X=3)= {8 \choose 3} 0.3^30.7^5=0.2541\)
• \( P(X \ge 1)=1-P(X=0)=1-.7^8=0.942\)
• \( E(X) = np = 8 \times 0.3=2.4 \)
• \( Sd(X)= \sqrt{npq}=\sqrt{8\times 0.30 \times 0.70}=1.3\)

Below you can see SOCR snapshots for this example:

• Example 2:

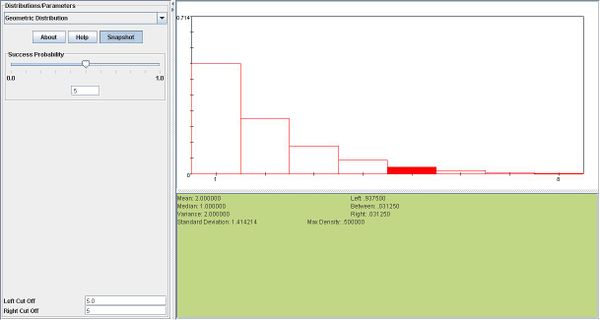
If the probabilities of having a male or female offspring are both 0.50, find the probability that a familiy's fifth child is their first son.

• Answer:
• \( X \sim geometric(0.5)\), \(P(X=5)= (.5)^4 \times .5=0.03125\)

• Example 3:

A complex electronic system is built with a certain number of backup components in its subsystem. One subsystem has 4 identical components, each with probability of 0.20 of failing in less than 1000 hours. The subsystem will operate if at least 2 of the 4 components are operating. Assume the components operate independently.

• Answer:
  • a. Find the probability that exactly 2 of the 4 components last longer than 1000 hours.
  • b. Find the probability that the subsystem operates longer than 1000 hours.
  • a. \(X \sim b(4,0.8) \), \( P(X=2)= {4 \choose 2} 0.8^2 0.2^2=0.1536\)

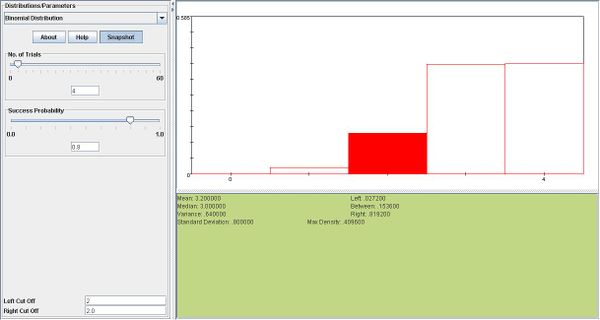
• • b. \(P(X\ge 2)= {4 \choose 2} 0.8^2 0.2^2+{4 \choose 3} 0.8^3 0.2^1+{4 \choose 4} 0.8^4=0.9728\)

• Example 4:

Suppose that 30% of the applicants for a certain industrial job have advanced training in computer programming. Applicants are interviewed sequentially and are selected at random from the pool. Find the probability that the firs applicant having advanced raining in computer programming is found on the fifth interview.

• Answer:
• \( X \sim geometric(0.3) \)\(P(X=5)=0.7^4 0.3=0.07203\) where X represents the number of trials.

• Example 5:

Refer to example 4. What is the expected number of applicants who need to be interviewed in order to find the first one with advanced training in computer proramming?

• Answer:

\( E(X)=\frac{1}{p}=\frac{1}{0.30}=3.33\)

• Example 6:

A missile protection system consists of n radar sets operating independently, each with probability 0.90 o detecting a missile entering a zone. a. If n= and a missile enters the zone what is the probability that exactly 4 radar sets detect the missile? At least one? b. How large must n be if we require the probability of detecting a missile to be 0.999?

• a. \(X \sim b(5,0.90). P(X=4)= {5 \choose 4} 0.9^4 0.1^1=0.32805\)

• • \(P(X\ge 1)= 1-P(X=0)= 1- 0.1^4=0.9999\)

• • b. \(P(X=0)=.001, 0.001= 0.1^n n= 3.\)
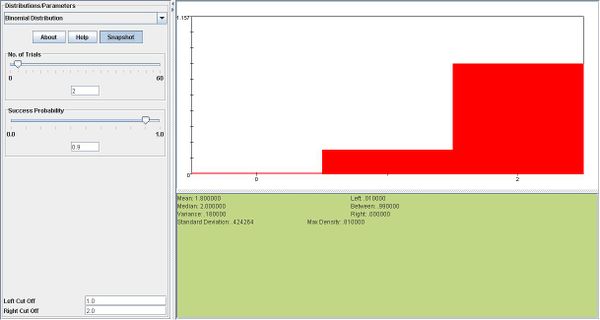
• In the first snapshot below, where\(n=2, P(X\ge1)=0.99,\) which is too small. In the second snapshot, we can see that when n is increased to 3, \(P(X\ge1)\) increases to nearly 1.

• Example 7:

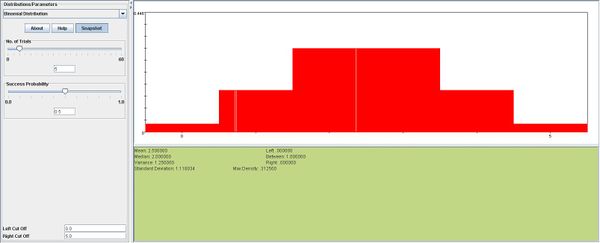
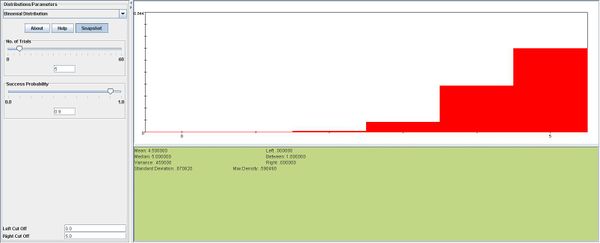
Construct a probability histogram for the binomial probability distribution for each of the following: n=5,p=0.1, n=5,p=0.5, m=5,n=0.9. What do you observe? Explain.

• Answer:

We observe that if p=0.5 the distribution resembles the normal distribution, with mean \(np=0.25\). Values above and below the mean are distributed symmetrically around the mean. Also, the probability histograms for p=0.1 and p=0.9 are mirror images of each other.

• Example 8:

On a population of consumers, 60% prefer a certain brand of ice cream. If consumers are randomly selected,

• a. what is the probability that exactly 3 people have to be interviewed to encounter the first consumer who prefers this brand of ice cream?

• b. what is the probability that at least 3 people have to be interviewed to encounter the first consumer who prefers this brand of ice cream?

• Answer:
• a. \( X \sim geometric(0.6) \)\(P(X=3)=0.4 \times 0.4 \times 0.6=0.096\)
• b. Let's first find the probability that at least 3 people will NOT have to be interviewed to encounter the first case.

\(P(X=1) + P(X=2) = 0.6+0.4 \times 0.6 = 0.84\)

• Now we subtract this from 1 to find the complement, which is the event that at least 3 people WILL have to be interviewed to find the first case\[1-0.84= 0.16\]

• Example 9:

The alpha marketing research company employs consumer panels to explore preferences for new products. The current inquiry involves a taste test comparison between a standard brand A vanilla ice cream and a new one of reduced sugar. The company recruits panels of five consumers at a time and determines how many of the five prefer the new product. Their objective is to obtain a panel of five in which all five consumers prefer the new product. The actual probability that an individual will prefer the new product is 0.40. a. What is the probability that all five consumers will prefer the new product? b. What is the exact probability that alpha will go through 60 panels (each of five people) without finding a single panel of five which unanimously prefer the new product?

• Answer:
• a. \( X \sim b(5,0.4) \), \( P(X=5)= {5 \choose 5} 0.4^5 0.6^0=0.01024\)

• b. In this part we will look at every group of 5 people as one unit. We will denote success as the event that all 5 people in a group prefer the new product, and failure as the event that at least one person in a group does not prefer the new product. Therefore, \(p=0.01024\). So,

\( X \sim geometric(0.01024) \)\(P(X=60)= (1-.01024)^60 = 53.9%\)

• Below you can see a SOCR snapshot for this example:

• Example 10:
• Answer:
• a. We will denote the number of unbruised peaches in our first selection X, and the number of unbruised peaches in our second selection Y. \(P(shipment=A)=\)P(all four peaches are unbruised)+P(three of the peaches are unbruised) X P(four additional peaches are unbruised)= \(P(X=4)+P(X=3)\times P(Y=4).\)
• \( X \sim b(4,0.9) \), \( P(X=4)= {4 \choose 4} 0.9^4 0.1^0= 0.6561\)
• \( Y \sim b(4,0.9) \), \( P(Y=3)= {4 \choose 3} 0.9^3 0.1^1= 0.2916\)
• \( Y \sim b(4,0.9) \), \( P(Y=4)= {4 \choose 4} 0.9^4 0.1^0= 0.6561\)

Therefore, \(P(shipment=A)=0.6561+ (0.2916)(0.6561)=0.8474 <center>[[Image: SOCR_Activities_Binomial_Christou_example10_a.jpg|600px]]</center> *b.<math>P(Shipment=C)=\)P(three of the first four peaches are unbruised) X P(zero or one of the additional four peaches are unbruised) +P(two or fewer of the first four peaches are unbruised). The first selection of peaches = X. The second selection=Y.

• \( X \sim b(4,0.9) \), \( P(X=3)= {4 \choose 3} 0.9^3 0.1^1= 0.2916\)
• \( Y \sim b(4,0.9) \), \( P(Y=0)= {4 \choose 0} 0.9^0 0.1^4= 0.0001\)
• \(P(Y=1)={4 \choose 1} 0.9^1 0.1^3=0.0009\)

Therefore \(P(Y=0 or 1) = 0.0001+.0009=0.001.\)

• \(P(X\le2)=P(X=0)+P(X=1)+P(X=2)= {4 \choose 0} 0.9^0 0.1^4 + {4 \choose 1} 0.9^1 0.1^3+{4 \choose 2} 0.9^2 0.1^2= 0.0523\)

Therefore P(shipment=C)=\((0.2916 \times 0.001)+.0523 = 0.052\)

600px

• Example 11:
• Answer:
• a. We want our system to function, so we would prefer a system with the highest probability of operating. A system will operate if at least half of its components function.
• If n=3, P(functioning when n=3)=\(P(X\ge 2). \)

\(X \sim b(3,0.40). P(X \ge2)= P(X=2)+P(X=3)= {3 \choose 2} 0.4^2 0.6^1+{3 \choose 3} 0.4^3 0.6^0= 0.352\)

• If n=5, P(functioning when n=5)=\(P(X\ge 3). \)

\(X \sim b(5,0.40). P(X \ge3)= P(X=3)+P(X=4)+P(X=5)= {5 \choose 3} 0.4^3 0.6^2+{5 \choose 4} 0.4^4 0.6^1+{5 \choose 5} 0.4^5 0.6^0=0.31744\)

• Therefore it is better to have 3 components, because we will have a better chance of having a system that operates.
• b. Again, \(X \sim b(200,0.40).\) mean=expected value = \(np=200 \times 0.4 = 80; SD=\sqrt{npq}=\sqrt{200 \times 0.4 \times 0.5}=6.3245\)