SOCR EduMaterials Activities Central Limit Theorem Chi square examples
Revision as of 15:59, 14 May 2007 by Create90215 (talk | contribs)
- Answer:
- a. false, the standard deviation of the sample mean is \(\frac{\sigma}{\sqrt n}\). Thus as the sample size increases, n increases, and as n increases, the standard deviation decreases.
- b. True
- c. False, standard deviation of the sample mean is \(\frac{\sigma}{\sqrt n}\)
- d. True, the standard deviation of the total of a sample of n observations is \(n\sqrt \sigma\); but the standard deviation of the sample mean is \(\frac{\sigma}{\sqrt n}.\)Unless n is one, the standard deviation of the total of a sample of n observations exceeds the standard deviation of the sample mean.
- e. False, let's assume \(\sigma=2\) and \(n=2\). In this case, the z-score for \(P(\overline{X} > 4)\) would be -2.828 while the z-score for \(P(X>4)\) would be -2. \(P(Z>-2.828) > P(Z>-2) \). Therefore the statement is false.
- Answer:
- a. \(P(X \ge 1000)= P(X=1000)+P(X=1001)+....+P(X=1500)= (1500 \choose 1000) \times (.7)^1000 \times (.3)^500 + (1500 \choose 1001) \times (.7)^1001 \times (.3)^499 + ...+(1500 \choose 1500) \times (.7)^1500 \times (.3)^0 = \summation (\1500 \choose X) \times (.7)^X \times (.3)^1500-X\)
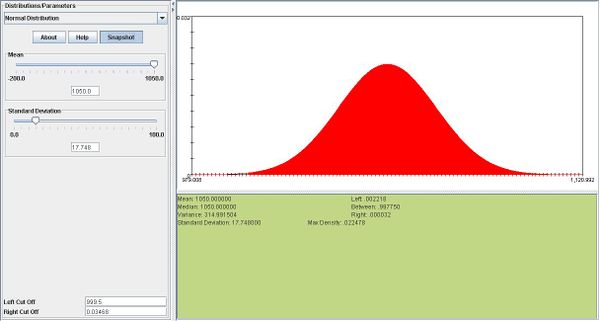
- b. We can use the normal approximation to binomial\[\mu = np = 1500 \times 0.70 = 1050.\] and \(\sigma = \sqrt npq = \sqrt1500 \times 0.7 \times 0.3= 17.748.\)
\(P(X \ge 1000)= P(Z> \frac{999.5-1050}{17.748}=P(Z>-2.845)=.9977\)
- Below you can see a snapshot for this approximation:
- ’’’Answer:’’’
- a. \(\overline{X} \sim N(8, \frac{20}{\sqrt400}). P(\overline{X} <6.50) =P(Z<-1.5)=.933\)
Below you can see a snapshot for this part:
- b. ??
- c. The central limit theorem states that the sample mean approaches the normal distribution as the sample size gets bigger. Usually, if \( n \ge 30\)we can assume that the sample mean approaches the normal distribution. In this case \(n=400\). Therefore n satisfies the requirement of a large n.
- d. \(\overline{X} \sim N(8,1). According to the snapshot below, the middle 80% of this distribution is (6.721,9.279). Therefore <math>w=8-6.721 =1.29\)
- e. \(T \sim N(n\mu,\sigma\sqrt(n)). \)In this case, \(T \sim N(3200,400).\) We know that P(T>b) =.975. So now we need to find the 97.5th percentile of this distribution using SOCR. According to the SOCR snapshot below, the 97.5th percentile of this distribution is 3984. Therefore b=3984.
- ’’’Answer:’’’
- a. \(\overline{X} \sim N(\mu, \frac{\sigma}{\sqrtn}</math. In this case, <math>\overline{X} \sim N(80000, 4518.48)\).
- b. We can find the answer using SOCR. The answer is 0.004032. Please see snapshot below:
- c. We can find the answer right away using SOCR. Please see snapshots below:
55.6% for one hour vs. 86.6% for sample mean. Therefore the sample mean is more likely to be greater than 75000 hours.
- ’’’Answer:’’’
- a. According to the SOCR snapshot below, the 75th percentile is 0.006115.
- b.