SOCR EduMaterials Activities Central Limit Theorem Chi square examples

• Answer:
• a. false, the standard deviation of the sample mean is \(\frac{\sigma}{\sqrt n}\). Thus as the sample size increases, n increases, and as n increases, the standard deviation decreases.
• b. True
• c. False, standard deviation of the sample mean is \(\frac{\sigma}{\sqrt n}\)
• d. True, the standard deviation of the total of a sample of n observations is \(n\sqrt \sigma\); but the standard deviation of the sample mean is \(\frac{\sigma}{\sqrt n}.\)Unless n is one, the standard deviation of the total of a sample of n observations exceeds the standard deviation of the sample mean.
• e. False, let's assume \(\sigma=2\) and \(n=2\). In this case, the z-score for \(P(\overline{X} > 4)\) would be -2.828 while the z-score for \(P(X>4)\) would be -2. \(P(Z>-2.828) > P(Z>-2) \). Therefore the statement is false.

• Answer:
• a. \(P(X \ge 1000)= P(X=1000)+P(X=1001)+....+P(X=1500)= (1500 \choose 1000) \times (.7)^1000 \times (.3)^500 + (1500 \choose 1001) \times (.7)^1001 \times (.3)^499 + ...+(1500 \choose 1500) \times (.7)^1500 \times (.3)^0 = \summation (\1500 \choose X) \times (.7)^X \times (.3)^1500-X\)
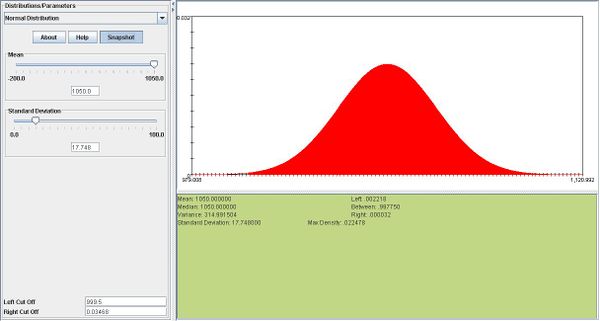
• b. We can use the normal approximation to binomial\[\mu = np = 1500 \times 0.70 = 1050.\] and \(\sigma = \sqrt npq = \sqrt1500 \times 0.7 \times 0.3= 17.748.\)

\(P(X \ge 1000)= P(Z> \frac{999.5-1050}{17.748}=P(Z>-2.845)=.9977\)

• Below you can see a snapshot for this approximation:

• Answer:
• a. \(\overline{X} \sim N(8, \frac{20}{\sqrt400}). P(\overline{X} <6.50) =P(Z<-1.5)=.0667\)
• Below you can see a snapshot for this part:

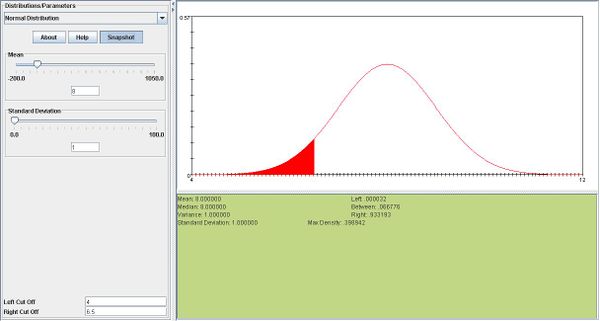
• b. ??
• c. The central limit theorem states that the sample mean approaches the normal distribution as the sample size gets bigger. Usually, if \( n \ge 30\)we can assume that the sample mean approaches the normal distribution. In this case \(n=400\). Therefore n satisfies the requirement of a large n.
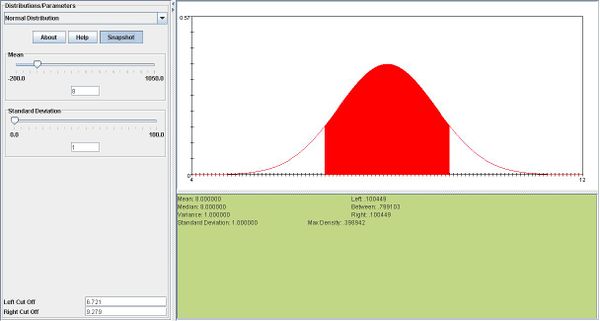
• d.\(\overline{X} \sim N(8,1).\)According to the snapshot below, the middle 80% of this distribution is (6.721,9.279). Therefore \(w=8-6.721 =1.29\)

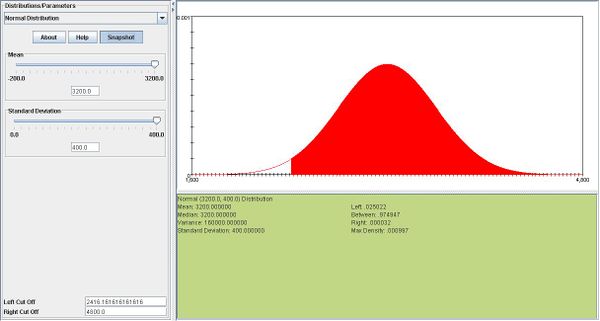
• e. \(T \sim N(n\mu,\sigma\sqrt n).\) In this case, \(T \sim N(3200,400).\) We know that \(P(T>b) =.975.\)So now we need to find the 97.5th percentile of this distribution using SOCR. According to the SOCR snapshot below, the 97.5th percentile of this distribution is 3984. Therefore b=3984.

• Answer:
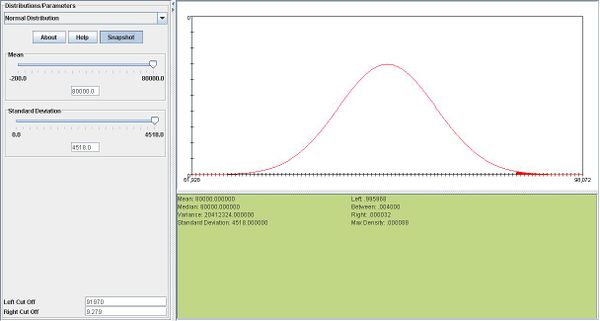
• a. \(\overline{X} \sim N(\mu, \frac{\sigma}{\sqrt n }\). In this case, \(\overline{X} \sim N(80000, 4518.48)\).
• b. We can find the answer using SOCR. The answer is 0.004032. Please see snapshot below:

• c. We can find the answer right away using SOCR. Please see snapshots below:

This is the distribution for \(X\) This is the distribution for \(\overline{X}\)

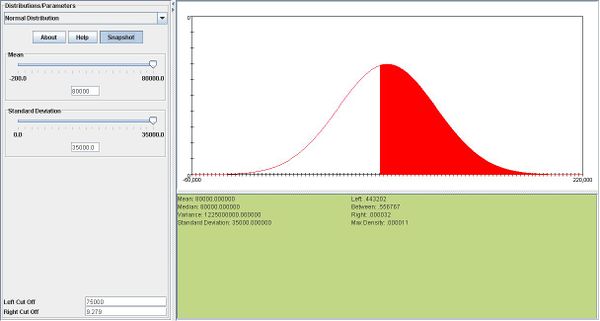
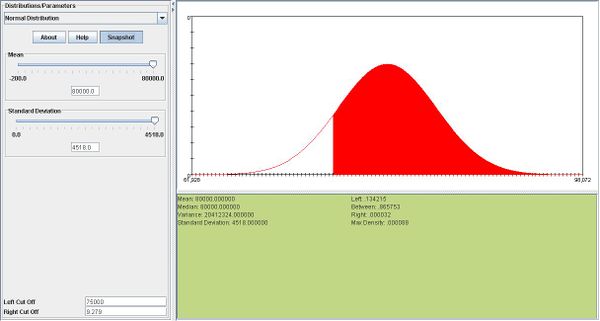
• The probabilities are 55.6% for one hour vs. 86.6% for sample mean. Therefore the sample mean is more likely to be greater than 75000 hours.

• Answer:
• a. According to the SOCR snapshot below, the 75th percentile is 0.006115.

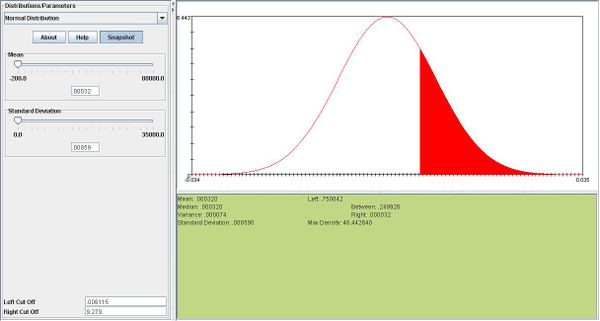
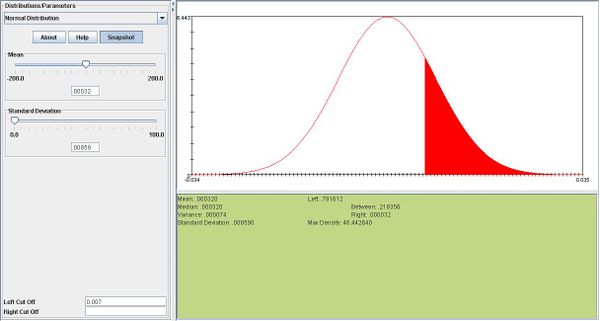
• b.\(P(X>.01)=.13.\)We can see this in the snapshot below:

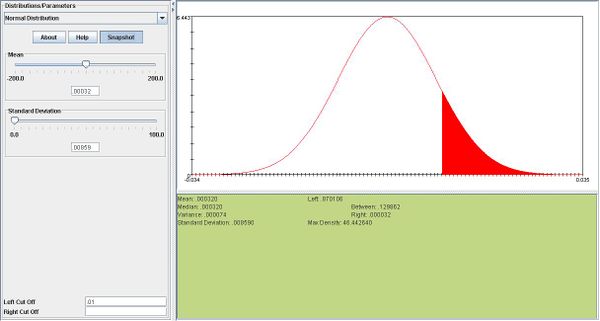
• \(P(R=2)= (5 \choose 2) \times .13^2 \times .87^3= 0.11128. \)

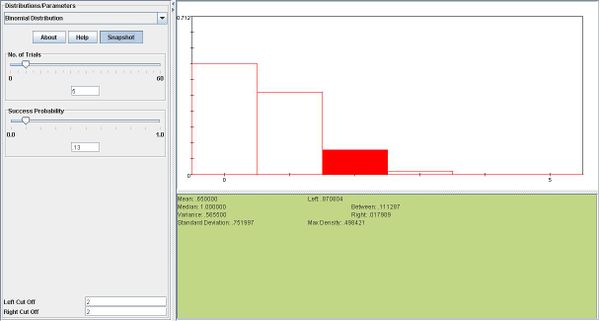
• c.

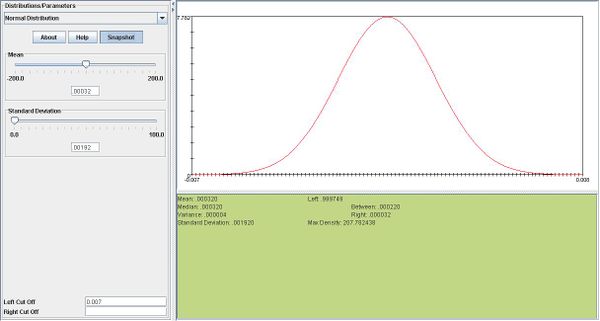
i. \(X \sim N(.00032,.00192)\)

ii. \(P(\overline{X}>.005)=.0074\)

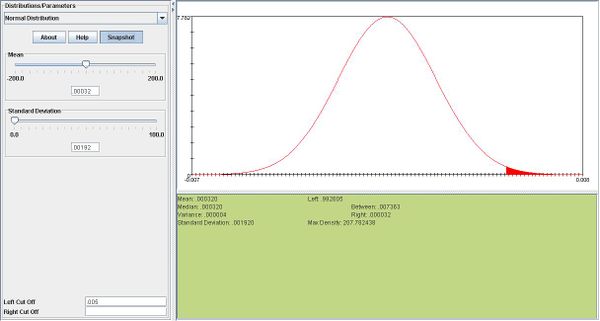
iii.One day's return is more likely to be greater than .007. The probabilities are 0.21 for \(X\) vs. .00022 for \(\overline{X}\).

This is the snapshot for \(P(X>.007)\) This is the snapshot for \(P(\overline{X}>.007)\)