AP Statistics Curriculum 2007 Exponential
Contents
[hide]General Advance-Placement (AP) Statistics Curriculum - Exponential Distribution
Exponential Distribution
Definition: Exponential distribution, also known as Mean-Time-To-Failure distribution, is a special case of the gamma distribution. Whereas the gamma distribution is the waiting time for more than one event, the exponential distribution describes the time between a single Poisson event.
Probability density function: For \(X\sim \operatorname{Exponential}(\lambda)\!\), the exponential probability density function is given by
\[\lambda e^{-\lambda x}\!\]
where
- e is the natural number (e = 2.71828…)
- \(\lambda\) is the mean time between events
- x is a random variable
Cumulative density function: The exponential cumulative distribution function is given by
\[1-e^{-\lambda x}\!\]
where
- e is the natural number (e = 2.71828…)
- \(\lambda\) is the mean time between events
- x is a random variable
Moment generating function: The exponential moment-generating function is
\[M(t)=(1-\frac{t}{\lambda})^{-1}\]
Expectation: The expected value of a exponential distributed random variable x is
\[E(X)=\frac{1}{\lambda}\]
Variance: The exponential variance is
\[Var(X)=\frac{1}{\lambda^2}\]
Applications
The exponential distribution occurs naturally when describing the waiting time in a homogeneous Poisson process. It can be used in a range of disciplines including queuing theory, physics, reliability theory, and hydrology. Examples of events that may be modeled by exponential distribution include:
- The time until a radioactive particle decays
- The time between clicks of a Geiger counter
- The time until default on payment to company debt holders
- The distance between roadkills on a given road
- The distance between mutations on a DNA strand
- The time it takes for a bank teller to serve a customer
- The height of various molecules in a gas at a fixed temperature and pressure in a uniform gravitational field
- The monthly and annual maximum values of daily rainfall and river discharge volumes
Example
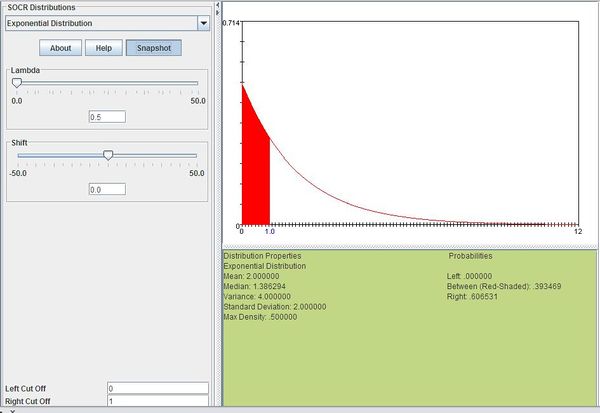
Suppose you usually get 2 phone calls per hour. Compute the probability that a phone call will arrive within the next hour.
2 phone calls per hour means that we would expect one phone call every 1/2 hour so \(\lambda=0.5\). We can then compute this as follows:
\[P(0\le X\le 1)=\sum_{x=0}^1 0.5e^{-0.5x}=0.393469\]
The figure below shows this result using SOCR distributions
- SOCR Home page: http://www.socr.ucla.edu
"-----
Translate this page: