SMHS LinearModeling MLR
SMHS Linear Modeling - Multiple Linear Regression
In this section, we expand our previous discussion of linear modeling, review, and demonstrate computing and visualizing the regression-model coefficients (effect-sizes), (fixed-effect) linear model assumptions, examination of residual plots, and independence.
Questions:
- Are there (linear) associations between predictors and a response variable(s)?
- When to look for linear relations and what assumptions play role?
Let’s use some of the data included in the Appendix. Snapshots of the first few rows in the data are shown below:
| Genotype | Race | Subject | Weight | Index | Subject | Day | Treatment | Obs |
| A | 1 | 1 | 8 | 1 | 13 | Day1 | B | 6.472687 |
| A | 1 | 2 | 9 | 2 | 14 | Day1 | B | 7.01711 |
| A | 1 | 3 | 11 | 3 | 15 | Day1 | B | 6.2007154 |
| A | 1 | 4 | 12 | 4 | 16 | Day1 | B | 6.6139285 |
| A | 1 | 5 | 10 | 5 | 17 | Day1 | A | 6.8299686 |
| A | 2 | 1 | 17 | 6 | 18 | Day1 | A | 7.387583 |
| ... | ... |
Eyeballing the data may suggest that Race "2" subjects may have higher "Weights" (first dataset), or "Treatment A" yields higher "Observations" (second dataset). However, this cursory observation may be incorrect, as we may be looking at a small/exceptional sub-sample of the entire population. Data-driven linear modeling allows us to quantify such patterns and compute probability values expressing the strength of the evidence in the data to make such conclusions. In a nutshell, we express relationships of interest (e.g., weight as a function of race, or Observation as a function of treatment) using a linear function as an analytical representation of these inter-variable relations:
Weight ~ Race, Weight ~ Genotype, Obs ~ Treatment, Obs ~ Day, etc.
W = a +b*R,
This "~" (tilde) notation implies "Weight predicted by Race" or "Observation as a linear function of Treatment". The "dependent variable" (a measurable response) on the left is predicted by the factor on the right acting as an "independent variable", co-variate, predictor, "explanatory variable", or "fixed effect".
Often times inter-dependencies may not be perfect, deterministic, or rigid (like in the case of predicting the Area of a disk knowing its radius, or predicting the 3D spatial location of a planet having a precise date and time). Weight may not be completely and uniquely determined by Race alone, as many different factors play role (genetics, environment, aging, etc.) Even if we can measure all factors we can identify as potentially influencing Weight, there will still be intrinsic random variability into the observed Weight measures, which can’t be control for. This intrinsic random variation may be captured and accounted for using "random" term at the end.
Weight ~ Race + ε~ D(m=0, s).
Epsilon "ε" represents the error term of predicting Weight by Gender alone and summarizes the aggregate impact of all factors aside from Race that impact individual’s Weight, which are experimentally uncontrollable or random. This formula is a schematic analytic representation of a linear model that we’re going to estimate, quantify, and use for prediction and inference. The right hand side splits the knowledge representation of Weight into 2 complementary components - a "fixed effect" for Race, which we understand and expect, and a "random effect" ("ε") what we don’t know well. (W ~ R represents the "structural" or "systematic" part of the linear model and "ε" stands for the "random" or "probabilistic" part of the model.
R Experiment (See Appendix)
mydata1 <- data.frame(
Subject = c(13, 14, 15, 16, 17, 18),
Day = c("Day1", "Day1", "Day1", "Day2", "Day2", "Day2"),
Treatment = c("B", "B", "B", "A", "A", "A"),
Obs = c(6.472687, 7.017110, 6.200715, 6.613928, 6.829968, 7.387583)
)
We construct an R frame object1 concatenating 3 data-elements for 6 subjects, and saving it into "mydata1."
| Subject | Day | Treatment | Obs |
| 13 | Day1 | B | 6.472687 |
| 14 | Day1 | B | 7.017110 |
| 15 | Day1 | B | 6.200715 |
| 16 | Day2 | A | 6.613928 |
| 17 | Day2 | A | 6.829968 |
| 18 | Day2 | A | 7.387583 |
Using the linear model Obs ~ Treatment + ε, we can invoke the linear modeling function lm()2 . The "ε" term is implicit in all models so it need not be specified.
lm.1 <- lm(Obs ~ Treatment, mydata1)
The assignment operator "<-" stores the linear model result in object lm.1. For these data (the data object is "mydata1"), this model expresses Obs as a function of Treatment. To inspect the result of the linear model use the "summarize" function summary():
AIC(lm.1); BIC(lm.1) summary(lm.1)
The result is:
Call:
lm(formula = Obs ~ Treatment, data = mydata1)
Residuals:
1 2 3 4 5 6
-0.10342 0.44100 -0.37540 0.03782 -0.27881 0.27881
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.1088 0.2507 28.350 9.21e-06 ***
TreatmentB -0.5327 0.3071 -1.734 0.158
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3546 on 4 degrees of freedom
Multiple R-squared: 0.4293, Adjusted R-squared: 0.2866
F-statistic: 3.008 on 1 and 4 DF, p-value: 0.1579
The report shows:
- The model analytical formula specified by the lm() call.
- The residuals (errors, discrepancies between observed and model-predicted outcomes).
- The coefficients of the fixed effects (predictors, explanatory variables).
- And finally, the overall model quality (describing the ability of the model to describe the linear relations in these data). "Multiple R-squared" refers to the R2 statistic that measures the "variance explained by the model" or "variance accounted for by the model". 0≤R2≤1, in our result, R2 = 0.4293, which is good, but not great. In essence, 42.93% of the data variability may be explained by this specific (best linear fit) model. In this case, the model solely relies on "Treatment" (fixed effect) to explain Obs (outcome). So, the R2 reflects how much of the Obs variance is accounted for by different Treatments (A or B).
Models with high R2 values are preferred, subject to 2 conditions:
- What is considered a high R2 value is relative and depends on study/application.
- When the study phenomenon is highly deterministic, R2 values can approach 1.
Higher number of explanatory variable and higher model-complexity tend to yield higher R2 values, but are more difficult to interpret.
The "Adjusted R-squared" value is a modified R2 value that normalizes the total variance "explained" by the model by the number of fixed effects included in the model. Larger number predictors will lower the "Adjusted R-squared". The adjusted R2adj = 0.2866, but in general, R2adj can be much lower when the model includes many fixed effects.
The statistical test of "model significance" is quantified by the output "F-statistic: 3.008 on 1 and 4 DF, p-value: 0.1579". Under a null hypothesis where the model captures little or no information about the process, the probability value quantifies the data-driven evidence to reject the null and accept an alternative stating that this model does capture useful patterns in the data. Specifically, the p-value represents the conditional probability under the condition that the null hypothesis is true. In this case,
- The null hypothesis is Ho: "Treatment has no effect on Obs".
- Alternative research Hypothesis is H1: "Treatment has effect on Obs".
This p-value is 0.1579, and the linear model fails to reject the null hypothesis. This leaves open the possibility that Treatment may have no effect on Obs (just based on using these 6 data points).
However, if the p-value was much smaller, and assuming Ho were true, then this data would be less likely to be observed in reality (hence we would interpret small p-values as showing that the alternative hypothesis "Treatment affects Obs" as more likely and the model result is "statistically significant").
There is a distinction between the overall "model-significance" (as quantified by the p-value at the very bottom of the output, which considers all effects together) and the p-value of individual effects (coefficients table including significance for each predictor).
The model F-statistic and the degrees of freedom are in 1-1 correspondence with the p-value – the latter is computed as the right tail probability for an F(df1,df2) distribution corresponding to the F-statistics (critical value). To report the overall model inference in this case, we can state:
"Using a simple linear model of Obs as a function of Treatment, the model was not significant (F(1,4)=3.001, p>0.15), which indicates that "Treatment" may not be a critical explanatory factor describing the "Obs" outcome."
To examine the coefficient table for (lm.1 model).
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.1088 0.2507 28.350 9.21e-06 ***
TreatmentB -0.5327 0.3071 -1.734 0.158
The overall model p-value (0.1579) is similar to the p-value quantifying the significance of the "Treatment" factor to explain Obs. This is because the model had only one fixed effect ("Treatment" itself). So, the significance of the overall model is the same as the significance for this coefficient (subject to rounding error).
In the presence of multiple fixed effects, the overall model significance will be different from the significance of each coefficient corresponding to a specific covariate.
Why does the report show "TreatmentB" not "Treatment"? The estimate of the "(Intercept)" is 7.1088. Let’s look at the mean Obs values within each of the 2 Treatment groups (A and B):
# Model: lm.1 <- lm(Obs ~ Treatment, mydata1) mean(mydata1[mydata1$\$$Treatment=="A",]$\$$Obs) > 7.108776
mean(mydata1[mydata1$\$$Treatment=="B",]$\$$Obs) > 6.57611 # in general, subsetting3 can be accomplished by: subset_data <- mydata1[ which(mydata1$\$$Treatment=='A' & mydata1$\$$Day=='Day2'),]
The mean of the Obs values for {Treatment=A} is the same as the "Intercept" term.
The estimate for "TreatmentB" is negative (-0.5327). Note that:
7.108776 - 0.5327 = 6.57611,
which is the mean of the "TreatmentB" cohort. Thus,
the estimate for "(Intercept)" represents for the "TreatmentA" category, and
the estimate for "TreatmentB" represents the difference between the "Treatment" "A" and "B" categories.
Analytically, the linear models represent "linear" associations, as in the plot below:
mydata2 <- data.frame(
Subject = c(13, 14, 15, 16, 17, 18),
Day = c("Day1", "Day1", "Day1", "Day1", "Day1", "Day1"),
Treatment = c(2, 2, 2, 2, 1, 1),
Obs = c(6.472687, 7.017110, 6.200715, 6.613928, 6.829968, 7.387583)
)
plot(mydata2$\$$Treatment, mydata2$\$$Obs, main="Scatterplot Treatment vs. Obs",
xlab="Treatment", ylab="Obs ", pch=19)
# Add fit lines
abline(lm(mydata2$\$$Obs~mydata2$\$$Treatment), col="red")
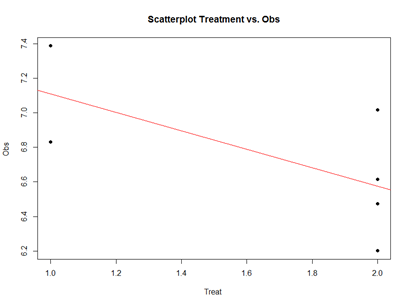
The linear model represents the difference between Treatments "A" and "B" as a slope. Going From Treatment "A" to "B" we go down -0.5327 (in terms of the units measuring the "Obs" variable), which is exactly the "TreatmentB" coefficient, relative to Treatment "A".
Treatment "A" acts as baseline (center of the local coordinate system) and is represented by the "(Intercept)". The difference between Treatments "A" and "B" is expressed as a slope heading down from 7.108776 by 0.5327. The p-values in the coefficient table correspond to the significance that each coefficient (intercept or Treatment) is "non-trivial".
In our case, the Intercept is significant (10-5), but the Treatment change (from A to B) is not (0.15). By default, the lm() function takes lexicographical ordering to determine which level (A or B) of the predictor (Treatment) comes first to label Treatment "A" as the intercept and "B" as the slope. Categorical differences like Treatment "A" and "B" can be expressed as slopes because difference between two categories is directly correlated with the slope between the two categories.
The advantage of representing difference between two categories as lines crossing the two categories is that it allows us to use the same computational principles for numeric and categorical variables. That is the same interpretations can be made for Treatment as for continuous (e.g., age) or discrete (e.g., dosage) covariates.
For example, using the MBL Data, we can examine player’s Weight as a function of Age. Save the data table as a text file "01a_data.txt" and load it in RStudio:
# data <- read.table('C:\\Users\\Dinov\\Desktop\\01a_data.txt',as.is=T, header=T)
# Data: https://umich.instructure.com/courses/38100/files/folder/data
data <- read.table('https://umich.instructure.com/courses/38100/files/folder/data/01a_data.txt',as.is=T, header=T)
attach(data)
# Weight = Age + e df.2 = data.frame(Age, Weight) lm.2 = lm(Weight ~ Age, df.2) summary(lm.2)
Call: lm(formula = Weight ~ Age, data = df.2) Residuals: Min 1Q Median 3Q Max -52.479 -14.489 -0.814 13.400 89.915 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 179.6684 4.3418 41.381 < 2e-16 *** Age 0.7672 0.1494 5.135 3.37e-07 *** ---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 20.75 on 1032 degrees of freedom Multiple R-squared: 0.02492, Adjusted R-squared: 0.02397 F-statistic: 26.37 on 1 and 1032 DF, p-value: 3.368e-07
The significance of the intercept is not very interesting, as it just specifies the baseline. However, the p-value in each (predictor) row evaluates whether the corresponding coefficient is significantly non-trivial. Trivial coefficients can be removed from the model. The intercept (179.6684) represents the predicted Weight for a player at Age 0, which doesn’t make sense for Baseball players, but it captures the constant impact of Age on Weight.
The interesting part is the coefficient of Age (0.7672), which is a significant predictor of Weight ($3.368\times 10^{-7}$). Thus, for every increase of age by 1 year, The Weight is expected to go up by 0.7 to 0.8 lbs.
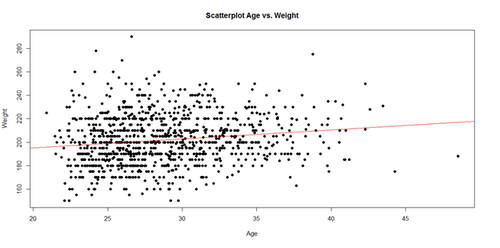
The regression line in the scatterplot represents the model-predicted mean Weight-gain with Age. The y-intercept (179.6684), for Age=0, and slope (0.7672) of the line represents the corresponding (Intercept and Age) coefficients of the model output.
plot(Age, Weight, main="Scatterplot Age vs. Weight", xlab="Age", ylab="Weight", pch=19) abline(lm(Weight ~ Age), col="red")
Interpreting Model Intercepts
The model estimates of the intercept may not always be useful. For instance, if we subtract the mean Age from each player's Age:
df.2$\$$Age.centered = df.2$\$$Age - mean(df.2$\$$Age) lm.2a = lm(Weight ~ Age.centered, df.2) summary(lm.2a)
This creates a new column in the data.frame (df.2) called Age.centered representing the Age variable with the mean subtracted from it. This is the resulting coefficient table from running a linear model analysis of this centered data:
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 201.7166 0.6452 312.648 < 2e-16 ***
Age.centered 0.7672 0.1494 5.135 3.37e-07 ***
Residual standard error: 20.75 on 1032 degrees of freedom
Multiple R-squared: 0.02492, Adjusted R-squared: 0.02397
F-statistic: 26.37 on 1 and 1032 DF, p-value: 3.368e-07
The intercept estimate has changed from 179.6684 (predicted Player Weight at birth, Age=0) to 201.7166 (predicted player Weight at mean Age). However, the slope and its significance (0.7672, 3.37x10-07) are unchanged and neither is the significance of the full model (3.368x10-07). So, centering the Age does not impact the nature of the linear model, it just changed the intercept that now points to the Weight at the mean Age.
As we have additional information for each MLB player, e.g., Team, Position, Height, Weight, Age) we can include additional factors into the linear model (lm.2a) to increase its explanatory power (R2 = 0.02492). We can start by adding:
Weight ~ Age + Height + e. lm.3 = lm(Weight ~ Age.centered + Height, df.2) summary(lm.3)
Call:
lm(formula = Weight ~ Age.centered + Height, data = df.2)
Residuals:
Min 1Q Median 3Q Max
-50.818 -12.148 -0.344 10.720 74.175
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -164.0141 17.2897 -9.486 < 2e-16 ***
Age.centered 0.9624 0.1252 7.690 3.43e-14 ***
Height 4.9626 0.2345 21.163 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 17.33 on 1031 degrees of freedom
Multiple R-squared: 0.3202, Adjusted R-squared: 0.3189
F-statistic: 242.8 on 2 and 1031 DF, p-value: < 2.2e-16
And them adding additional factors:
Weight ~ Age + Height + Position + Team + e. lm.4 = lm(Weight ~ Age.centered + Height+ Position + Team, df.2) summary(lm.4)
Call: lm(formula = Weight ~ Age.centered + Height + Position + Team, data = df.2) Residuals: Min 1Q Median 3Q Max -48.692 -10.909 -0.778 9.858 73.649 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -139.4055 18.8556 -7.393 3.04e-13 *** Age.centered 0.8906 0.1259 7.075 2.82e-12 *** Height 4.7175 0.2563 18.405 < 2e-16 *** PositionDesignated_Hitter 8.9037 4.4533 1.999 0.045842 * PositionFirst_Baseman 2.4237 3.0058 0.806 0.420236 PositionOutfielder -6.2636 2.2784 -2.749 0.006084 ** PositionRelief_Pitcher -7.7695 2.1959 -3.538 0.000421 *** PositionSecond_Baseman -13.0843 2.9638 -4.415 1.12e-05 *** PositionShortstop -16.9562 3.0406 -5.577 3.16e-08 *** PositionStarting_Pitcher -7.3599 2.2976 -3.203 0.001402 ** PositionThird_Baseman -4.6035 3.1689 -1.453 0.146613 TeamARZ 7.1881 4.2590 1.688 0.091777 TeamATL -1.5631 3.9757 -0.393 0.694278 TeamBAL -5.3128 4.0193 -1.322 0.186533 TeamBOS -0.2838 4.0034 -0.071 0.943492 TeamCHC 0.4026 3.9949 0.101 0.919749 TeamCIN 2.1051 3.9934 0.527 0.598211 TeamCLE -1.3160 4.0356 -0.326 0.744423 TeamCOL -3.7836 4.0287 -0.939 0.347881 TeamCWS 4.2944 4.1022 1.047 0.295413 TeamDET 2.3024 3.9725 0.580 0.562326 TeamFLA 2.6985 4.1336 0.653 0.514028 TeamHOU -0.6808 4.0634 -0.168 0.866976 TeamKC -4.7664 4.0242 -1.184 0.236525 TeamLA 2.8598 4.0817 0.701 0.483686 TeamMIN 2.1269 4.0947 0.519 0.603579 TeamMLW 4.2897 4.0243 1.066 0.286706 TeamNYM -1.9736 3.9493 -0.500 0.617370 TeamNYY 1.7483 4.1234 0.424 0.671655 TeamOAK -0.5464 3.9672 -0.138 0.890474 TeamPHI -6.8486 3.9949 -1.714 0.086778 TeamPIT 4.3023 4.0210 1.070 0.284890 TeamSD 2.6133 4.0915 0.639 0.523148 TeamSEA -0.9147 4.0516 -0.226 0.821436 TeamSF 0.8411 4.0520 0.208 0.835593 TeamSTL -1.1341 4.1193 -0.275 0.783132 TeamTB -2.6616 4.0944 -0.650 0.515798 TeamTEX -0.7695 4.0283 -0.191 0.848556 TeamTOR 1.3943 4.0681 0.343 0.731871 TeamWAS -1.7555 4.0038 -0.438 0.661142 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 16.78 on 994 degrees of freedom Multiple R-squared: 0.3858, Adjusted R-squared: 0.3617 F-statistic: 16.01 on 39 and 994 DF, p-value: < 2.2e-16
Notice the linear model coefficients, the corresponding p-values, and the overall model quality, at the bottom of the output change. Are these changed between the 2 models?
- new model (Weight ~ Age + Height + Position + Team + e.) vs.
- old model (Weight ~ Age + Height + e)?
These examples illustrate "multiple linear regression" as a linear modeling technique involving 1 response (dependent) variable expressed as a (affine) function of multiple predictor (independent) variables.
Footnotes
- 1 http://www.statmethods.net/input/datatypes.html
- 2 http://www.statmethods.net/advstats/glm.html
- 3 http://www.statmethods.net/management/subset.html
See next
- SOCR Home page: http://www.socr.umich.edu
Translate this page: