SOCR Data Dinov 072108 H Index Pubs
Contents
SOCR Data - Faculty Research Publications, Hirsch-Index and Citation Impact
Data Description
The data table below present the (total) publication counts and their corresponding citation impacts for 5 UCLA faculty (Toga, De Leeuw, Yuille, Dinov and Hansen). The Index column contains the ordered list of publications for all 5 faculty. The cell values included in a specific author-column contain the number of citations for that author for each index (i.e., for each of their publications). Note that for each author-column, these values are monotonically-decreasing. So, index i for author k and index j for author m represent completely different publications.
Sources
Data Interpretation
These data are not intended to compare, rank or evaluate any of the UCLA faculty included (or not included) in this table. The data are provided simply for the purpose of demonstrating various SOCR tools, applets, resources and to supplement existent learning activities (e.g., EBook). You can see the H-indexes and more graphs of the publications and impact for each of these faculty here: Toga, De Leeuw, Yuille, Dinov and Hansen, as of June 2008.
Probability of faculty promotion
Research publication play an important component of faculty performance evaluation and promotion. The formula used in sciences (statistics, biostatistics, biomath, etc.) for estimating the probability of faculty promotion (from assistant to associate, or from associate to full professor) is described below.
- See this video
- Log-odds-ratio: $$ \ln\left ( \frac{P(promotion=Yes)}{P(Promotion=No)}\right ) = intercept (-1.0, for\ assistant2associate, -3.0, for\ assocaite2full)$$
$$ + 0.01*(\# articles) + 0.01*(Courses\ taught)$$ $$-0.05*(student\ ratings, 0-100\% excellent) - 0.05*(refereed\ papers/year)$$ $$+ 1.0*(faculty\ service, 0-100\%) $$ $$-1.0*(institutional-correction-factor, 0 (NoMansU) to 1(Harvard), UMich=0.9).$$
- Example: $Log-odds-ratio = -3 + 0.01*(100) + 0.01*(10) -0.05*(20) - 0.05*(5) + 1.0*(10) -1.0*(0.9) = 5.95$. Thus, the odds of Promotion is $61:1$.
- Faculty scholarship also includes gransmanship. Grant PIship may be less common for statisticians, mathematicians (and other basic science disciplines) compared to health, biological, social, and engineering faculty. Many applied statisticians have portfolios of grants as core directors, investigators, biostatisticians, etc.
- Scholarly productivity is also important. Funded grants are enablers or accelerators of scholarship, certainly not as products of research. Scientific productivity includes specific outputs of one’s work that fill a niche, openly share ideas, provide software tools, learning modules, instructional resources, knowledge or services promoting the growth of the entire community, impact lives, enhance human experiences, or improve ambient environments.
Data Table
| Index | Toga | De_Leeuw | Yuille | Dinov | Hansen |
|---|---|---|---|---|---|
| 1 | 413 | 843 | 1055 | 65 | 712 |
| 2 | 352 | 301 | 280 | 54 | 216 |
| 3 | 327 | 292 | 250 | 46 | 137 |
| 4 | 315 | 174 | 200 | 45 | 66 |
| 5 | 289 | 135 | 161 | 42 | 30 |
| 6 | 276 | 134 | 132 | 33 | 27 |
| 7 | 259 | 92 | 125 | 32 | 25 |
| 8 | 256 | 91 | 97 | 26 | 20 |
| 9 | 236 | 86 | 75 | 24 | 19 |
| 10 | 203 | 85 | 73 | 17 | 17 |
| 11 | 189 | 79 | 64 | 15 | 14 |
| 12 | 181 | 76 | 62 | 13 | 10 |
| 13 | 180 | 73 | 61 | 11 | 9 |
| 14 | 167 | 70 | 59 | 10 | 9 |
| 15 | 166 | 70 | 57 | 9 | 8 |
| 16 | 166 | 67 | 48 | 9 | 7 |
| 17 | 161 | 63 | 37 | 8 | 7 |
| 18 | 151 | 60 | 34 | 7 | 7 |
| 19 | 150 | 60 | 30 | 5 | 6 |
| 20 | 147 | 58 | 29 | 5 | 6 |
| 21 | 146 | 58 | 23 | 5 | 6 |
| 22 | 124 | 56 | 23 | 4 | 5 |
| 23 | 113 | 54 | 22 | 4 | 5 |
| 24 | 110 | 53 | 19 | 4 | 5 |
| 25 | 108 | 51 | 19 | 4 | 4 |
| 26 | 105 | 50 | 18 | 4 | 3 |
| 27 | 99 | 49 | 16 | 4 | 3 |
| 28 | 98 | 49 | 14 | 4 | 3 |
| 29 | 88 | 49 | 13 | 4 | 3 |
| 30 | 88 | 46 | 12 | 4 | 3 |
| 31 | 83 | 45 | 11 | 3 | 3 |
| 32 | 82 | 45 | 11 | 3 | 3 |
| 33 | 82 | 45 | 8 | 3 | 3 |
| 34 | 81 | 42 | 8 | 3 | 2 |
| 35 | 80 | 41 | 7 | 2 | 2 |
| 36 | 78 | 40 | 7 | 2 | 2 |
| 37 | 73 | 40 | 7 | 2 | 1 |
| 38 | 71 | 39 | 7 | 2 | 1 |
| 39 | 70 | 38 | 6 | 2 | 1 |
| 40 | 68 | 37 | 6 | 2 | 1 |
| 41 | 66 | 37 | 6 | 2 | 1 |
| 42 | 65 | 37 | 5 | 2 | 1 |
| 43 | 65 | 36 | 5 | 2 | 1 |
| 44 | 62 | 35 | 5 | 2 | 1 |
| 45 | 62 | 35 | 5 | 2 | 1 |
| 46 | 61 | 35 | 5 | 2 | 1 |
| 47 | 60 | 35 | 5 | 2 | 1 |
| 48 | 60 | 33 | 4 | 2 | 1 |
| 49 | 60 | 33 | 4 | 1 | 1 |
| 50 | 58 | 30 | 4 | 1 | 1 |
| 51 | 57 | 30 | 4 | 1 | 1 |
| 52 | 56 | 29 | 3 | 1 | 1 |
| 53 | 54 | 28 | 3 | 1 | 0 |
| 54 | 54 | 28 | 2 | 1 | 0 |
| 55 | 54 | 27 | 2 | 1 | 0 |
| 56 | 54 | 27 | 2 | 1 | 0 |
| 57 | 53 | 27 | 2 | 1 | 0 |
| 58 | 52 | 27 | 2 | 1 | 0 |
| 59 | 51 | 27 | 2 | 1 | 0 |
| 60 | 49 | 24 | 1 | 1 | 0 |
| 61 | 49 | 24 | 1 | 1 | 0 |
| 62 | 48 | 24 | 1 | 1 | 0 |
| 63 | 46 | 23 | 1 | 1 | 0 |
| 64 | 46 | 23 | 1 | 1 | 0 |
| 65 | 46 | 22 | 1 | 0 | 0 |
| 66 | 45 | 22 | 1 | 0 | 0 |
| 67 | 45 | 22 | 1 | 0 | 0 |
| 68 | 45 | 22 | 0 | 0 | 0 |
| 69 | 45 | 21 | 0 | 0 | 0 |
| 70 | 44 | 21 | 0 | 0 | 0 |
| 71 | 42 | 21 | 0 | 0 | 0 |
| 72 | 42 | 20 | 0 | 0 | 0 |
| 73 | 42 | 20 | 0 | 0 | 0 |
| 74 | 42 | 20 | 0 | 0 | 0 |
| 75 | 41 | 20 | 0 | 0 | 0 |
| 76 | 40 | 19 | 0 | 0 | 0 |
| 77 | 40 | 18 | 0 | 0 | 0 |
| 78 | 40 | 18 | 0 | 0 | 0 |
| 79 | 40 | 18 | 0 | 0 | 0 |
| 80 | 40 | 18 | 0 | 0 | 0 |
| 81 | 39 | 17 | 0 | 0 | 0 |
| 82 | 39 | 17 | 0 | 0 | 0 |
| 83 | 38 | 16 | 0 | 0 | 0 |
| 84 | 38 | 16 | 0 | 0 | 0 |
| 85 | 38 | 16 | 0 | 0 | 0 |
| 86 | 37 | 16 | 0 | 0 | 0 |
| 87 | 37 | 16 | 0 | 0 | 0 |
| 88 | 37 | 16 | 0 | 0 | 0 |
| 89 | 37 | 16 | 0 | 0 | 0 |
| 90 | 37 | 16 | 0 | 0 | 0 |
| 91 | 37 | 16 | 0 | 0 | 0 |
| 92 | 35 | 15 | 0 | 0 | 0 |
| 93 | 35 | 15 | 0 | 0 | 0 |
| 94 | 35 | 15 | 0 | 0 | 0 |
| 95 | 34 | 15 | 0 | 0 | 0 |
| 96 | 33 | 15 | 0 | 0 | 0 |
| 97 | 33 | 15 | 0 | 0 | 0 |
| 98 | 33 | 15 | 0 | 0 | 0 |
| 99 | 33 | 15 | 0 | 0 | 0 |
| 100 | 33 | 15 | 0 | 0 | 0 |
| 101 | 32 | 14 | 0 | 0 | 0 |
| 102 | 31 | 14 | 0 | 0 | 0 |
| 103 | 31 | 14 | 0 | 0 | 0 |
| 104 | 30 | 14 | 0 | 0 | 0 |
| 105 | 30 | 14 | 0 | 0 | 0 |
| 106 | 30 | 14 | 0 | 0 | 0 |
| 107 | 29 | 14 | 0 | 0 | 0 |
| 108 | 28 | 13 | 0 | 0 | 0 |
| 109 | 28 | 13 | 0 | 0 | 0 |
| 110 | 28 | 13 | 0 | 0 | 0 |
| 111 | 28 | 13 | 0 | 0 | 0 |
| 112 | 27 | 13 | 0 | 0 | 0 |
| 113 | 27 | 13 | 0 | 0 | 0 |
| 114 | 27 | 13 | 0 | 0 | 0 |
| 115 | 27 | 13 | 0 | 0 | 0 |
| 116 | 26 | 13 | 0 | 0 | 0 |
| 117 | 26 | 12 | 0 | 0 | 0 |
| 118 | 26 | 12 | 0 | 0 | 0 |
| 119 | 26 | 12 | 0 | 0 | 0 |
| 120 | 25 | 12 | 0 | 0 | 0 |
| 121 | 25 | 12 | 0 | 0 | 0 |
| 122 | 25 | 11 | 0 | 0 | 0 |
| 123 | 25 | 11 | 0 | 0 | 0 |
| 124 | 25 | 11 | 0 | 0 | 0 |
| 125 | 24 | 10 | 0 | 0 | 0 |
| 126 | 24 | 10 | 0 | 0 | 0 |
| 127 | 24 | 10 | 0 | 0 | 0 |
| 128 | 24 | 10 | 0 | 0 | 0 |
| 129 | 23 | 10 | 0 | 0 | 0 |
| 130 | 23 | 9 | 0 | 0 | 0 |
| 131 | 23 | 9 | 0 | 0 | 0 |
| 132 | 22 | 9 | 0 | 0 | 0 |
| 133 | 22 | 9 | 0 | 0 | 0 |
| 134 | 22 | 9 | 0 | 0 | 0 |
| 135 | 22 | 9 | 0 | 0 | 0 |
| 136 | 21 | 9 | 0 | 0 | 0 |
| 137 | 21 | 9 | 0 | 0 | 0 |
| 138 | 21 | 8 | 0 | 0 | 0 |
| 139 | 21 | 8 | 0 | 0 | 0 |
| 140 | 21 | 8 | 0 | 0 | 0 |
| 141 | 20 | 8 | 0 | 0 | 0 |
| 142 | 20 | 8 | 0 | 0 | 0 |
| 143 | 19 | 8 | 0 | 0 | 0 |
| 144 | 19 | 8 | 0 | 0 | 0 |
| 145 | 19 | 8 | 0 | 0 | 0 |
| 146 | 19 | 8 | 0 | 0 | 0 |
| 147 | 19 | 8 | 0 | 0 | 0 |
| 148 | 18 | 8 | 0 | 0 | 0 |
| 149 | 18 | 8 | 0 | 0 | 0 |
| 150 | 18 | 7 | 0 | 0 | 0 |
| 151 | 18 | 7 | 0 | 0 | 0 |
| 152 | 18 | 7 | 0 | 0 | 0 |
| 153 | 18 | 7 | 0 | 0 | 0 |
| 154 | 18 | 7 | 0 | 0 | 0 |
| 155 | 17 | 7 | 0 | 0 | 0 |
| 156 | 17 | 6 | 0 | 0 | 0 |
| 157 | 17 | 6 | 0 | 0 | 0 |
| 158 | 17 | 6 | 0 | 0 | 0 |
| 159 | 17 | 6 | 0 | 0 | 0 |
| 160 | 17 | 6 | 0 | 0 | 0 |
| 161 | 17 | 6 | 0 | 0 | 0 |
| 162 | 17 | 5 | 0 | 0 | 0 |
| 163 | 17 | 5 | 0 | 0 | 0 |
| 164 | 16 | 5 | 0 | 0 | 0 |
| 165 | 16 | 5 | 0 | 0 | 0 |
| 166 | 16 | 5 | 0 | 0 | 0 |
| 167 | 16 | 5 | 0 | 0 | 0 |
| 168 | 16 | 5 | 0 | 0 | 0 |
| 169 | 15 | 5 | 0 | 0 | 0 |
| 170 | 15 | 5 | 0 | 0 | 0 |
| 171 | 15 | 5 | 0 | 0 | 0 |
| 172 | 15 | 5 | 0 | 0 | 0 |
| 173 | 15 | 5 | 0 | 0 | 0 |
| 174 | 14 | 4 | 0 | 0 | 0 |
| 175 | 14 | 4 | 0 | 0 | 0 |
| 176 | 14 | 4 | 0 | 0 | 0 |
| 177 | 14 | 4 | 0 | 0 | 0 |
| 178 | 14 | 4 | 0 | 0 | 0 |
| 179 | 14 | 4 | 0 | 0 | 0 |
| 180 | 13 | 4 | 0 | 0 | 0 |
| 181 | 13 | 4 | 0 | 0 | 0 |
| 182 | 13 | 4 | 0 | 0 | 0 |
| 183 | 13 | 4 | 0 | 0 | 0 |
| 184 | 13 | 4 | 0 | 0 | 0 |
| 185 | 13 | 4 | 0 | 0 | 0 |
| 186 | 13 | 4 | 0 | 0 | 0 |
| 187 | 13 | 4 | 0 | 0 | 0 |
| 188 | 13 | 4 | 0 | 0 | 0 |
| 189 | 13 | 3 | 0 | 0 | 0 |
| 190 | 12 | 3 | 0 | 0 | 0 |
| 191 | 12 | 3 | 0 | 0 | 0 |
| 192 | 12 | 3 | 0 | 0 | 0 |
| 193 | 12 | 3 | 0 | 0 | 0 |
| 194 | 12 | 3 | 0 | 0 | 0 |
| 195 | 12 | 3 | 0 | 0 | 0 |
| 196 | 11 | 3 | 0 | 0 | 0 |
| 197 | 11 | 3 | 0 | 0 | 0 |
| 198 | 11 | 3 | 0 | 0 | 0 |
| 199 | 11 | 3 | 0 | 0 | 0 |
| 200 | 11 | 3 | 0 | 0 | 0 |
| 201 | 11 | 2 | 0 | 0 | 0 |
| 202 | 11 | 2 | 0 | 0 | 0 |
| 203 | 11 | 2 | 0 | 0 | 0 |
| 204 | 11 | 2 | 0 | 0 | 0 |
| 205 | 11 | 2 | 0 | 0 | 0 |
| 206 | 11 | 2 | 0 | 0 | 0 |
| 207 | 10 | 2 | 0 | 0 | 0 |
| 208 | 10 | 2 | 0 | 0 | 0 |
| 209 | 10 | 2 | 0 | 0 | 0 |
| 210 | 10 | 2 | 0 | 0 | 0 |
| 211 | 10 | 2 | 0 | 0 | 0 |
| 212 | 10 | 2 | 0 | 0 | 0 |
| 213 | 10 | 2 | 0 | 0 | 0 |
| 214 | 10 | 2 | 0 | 0 | 0 |
| 215 | 10 | 2 | 0 | 0 | 0 |
| 216 | 10 | 2 | 0 | 0 | 0 |
| 217 | 10 | 2 | 0 | 0 | 0 |
| 218 | 10 | 2 | 0 | 0 | 0 |
| 219 | 10 | 2 | 0 | 0 | 0 |
| 220 | 10 | 2 | 0 | 0 | 0 |
| 221 | 10 | 2 | 0 | 0 | 0 |
| 222 | 9 | 2 | 0 | 0 | 0 |
| 223 | 9 | 2 | 0 | 0 | 0 |
| 224 | 9 | 2 | 0 | 0 | 0 |
| 225 | 9 | 1 | 0 | 0 | 0 |
| 226 | 9 | 1 | 0 | 0 | 0 |
| 227 | 9 | 1 | 0 | 0 | 0 |
| 228 | 9 | 1 | 0 | 0 | 0 |
| 229 | 9 | 1 | 0 | 0 | 0 |
| 230 | 9 | 1 | 0 | 0 | 0 |
| 231 | 9 | 1 | 0 | 0 | 0 |
| 232 | 9 | 1 | 0 | 0 | 0 |
| 233 | 9 | 1 | 0 | 0 | 0 |
| 234 | 9 | 1 | 0 | 0 | 0 |
| 235 | 9 | 1 | 0 | 0 | 0 |
| 236 | 9 | 1 | 0 | 0 | 0 |
| 237 | 8 | 1 | 0 | 0 | 0 |
| 238 | 8 | 1 | 0 | 0 | 0 |
| 239 | 8 | 1 | 0 | 0 | 0 |
| 240 | 8 | 1 | 0 | 0 | 0 |
| 241 | 8 | 1 | 0 | 0 | 0 |
| 242 | 8 | 1 | 0 | 0 | 0 |
| 243 | 8 | 1 | 0 | 0 | 0 |
| 244 | 8 | 1 | 0 | 0 | 0 |
| 245 | 8 | 1 | 0 | 0 | 0 |
| 246 | 8 | 1 | 0 | 0 | 0 |
| 247 | 8 | 0 | 0 | 0 | 0 |
| 248 | 8 | 0 | 0 | 0 | 0 |
| 249 | 8 | 0 | 0 | 0 | 0 |
| 250 | 7 | 0 | 0 | 0 | 0 |
| 251 | 7 | 0 | 0 | 0 | 0 |
| 252 | 7 | 0 | 0 | 0 | 0 |
| 253 | 7 | 0 | 0 | 0 | 0 |
| 254 | 7 | 0 | 0 | 0 | 0 |
| 255 | 7 | 0 | 0 | 0 | 0 |
| 256 | 7 | 0 | 0 | 0 | 0 |
| 257 | 7 | 0 | 0 | 0 | 0 |
| 258 | 7 | 0 | 0 | 0 | 0 |
| 259 | 7 | 0 | 0 | 0 | 0 |
| 260 | 7 | 0 | 0 | 0 | 0 |
| 261 | 7 | 0 | 0 | 0 | 0 |
| 262 | 7 | 0 | 0 | 0 | 0 |
| 263 | 6 | 0 | 0 | 0 | 0 |
| 264 | 6 | 0 | 0 | 0 | 0 |
| 265 | 6 | 0 | 0 | 0 | 0 |
| 266 | 6 | 0 | 0 | 0 | 0 |
| 267 | 6 | 0 | 0 | 0 | 0 |
| 268 | 6 | 0 | 0 | 0 | 0 |
| 269 | 6 | 0 | 0 | 0 | 0 |
| 270 | 6 | 0 | 0 | 0 | 0 |
| 271 | 6 | 0 | 0 | 0 | 0 |
| 272 | 6 | 0 | 0 | 0 | 0 |
| 273 | 6 | 0 | 0 | 0 | 0 |
| 274 | 6 | 0 | 0 | 0 | 0 |
| 275 | 6 | 0 | 0 | 0 | 0 |
| 276 | 6 | 0 | 0 | 0 | 0 |
| 277 | 6 | 0 | 0 | 0 | 0 |
| 278 | 6 | 0 | 0 | 0 | 0 |
| 279 | 5 | 0 | 0 | 0 | 0 |
| 280 | 5 | 0 | 0 | 0 | 0 |
| 281 | 5 | 0 | 0 | 0 | 0 |
| 282 | 5 | 0 | 0 | 0 | 0 |
| 283 | 5 | 0 | 0 | 0 | 0 |
| 284 | 5 | 0 | 0 | 0 | 0 |
| 285 | 5 | 0 | 0 | 0 | 0 |
| 286 | 5 | 0 | 0 | 0 | 0 |
| 287 | 5 | 0 | 0 | 0 | 0 |
| 288 | 5 | 0 | 0 | 0 | 0 |
| 289 | 5 | 0 | 0 | 0 | 0 |
| 290 | 5 | 0 | 0 | 0 | 0 |
| 291 | 5 | 0 | 0 | 0 | 0 |
| 292 | 5 | 0 | 0 | 0 | 0 |
| 293 | 5 | 0 | 0 | 0 | 0 |
| 294 | 5 | 0 | 0 | 0 | 0 |
| 295 | 5 | 0 | 0 | 0 | 0 |
| 296 | 4 | 0 | 0 | 0 | 0 |
| 297 | 4 | 0 | 0 | 0 | 0 |
| 298 | 4 | 0 | 0 | 0 | 0 |
| 299 | 4 | 0 | 0 | 0 | 0 |
| 300 | 4 | 0 | 0 | 0 | 0 |
| 301 | 4 | 0 | 0 | 0 | 0 |
| 302 | 4 | 0 | 0 | 0 | 0 |
| 303 | 4 | 0 | 0 | 0 | 0 |
| 304 | 4 | 0 | 0 | 0 | 0 |
| 305 | 4 | 0 | 0 | 0 | 0 |
| 306 | 4 | 0 | 0 | 0 | 0 |
| 307 | 4 | 0 | 0 | 0 | 0 |
| 308 | 4 | 0 | 0 | 0 | 0 |
| 309 | 4 | 0 | 0 | 0 | 0 |
| 310 | 4 | 0 | 0 | 0 | 0 |
| 311 | 4 | 0 | 0 | 0 | 0 |
| 312 | 4 | 0 | 0 | 0 | 0 |
| 313 | 4 | 0 | 0 | 0 | 0 |
| 314 | 4 | 0 | 0 | 0 | 0 |
| 315 | 4 | 0 | 0 | 0 | 0 |
| 316 | 4 | 0 | 0 | 0 | 0 |
| 317 | 4 | 0 | 0 | 0 | 0 |
| 318 | 4 | 0 | 0 | 0 | 0 |
| 319 | 4 | 0 | 0 | 0 | 0 |
| 320 | 4 | 0 | 0 | 0 | 0 |
| 321 | 4 | 0 | 0 | 0 | 0 |
| 322 | 4 | 0 | 0 | 0 | 0 |
| 323 | 4 | 0 | 0 | 0 | 0 |
| 324 | 4 | 0 | 0 | 0 | 0 |
| 325 | 4 | 0 | 0 | 0 | 0 |
| 326 | 4 | 0 | 0 | 0 | 0 |
| 327 | 4 | 0 | 0 | 0 | 0 |
| 328 | 4 | 0 | 0 | 0 | 0 |
| 329 | 4 | 0 | 0 | 0 | 0 |
| 330 | 4 | 0 | 0 | 0 | 0 |
| 331 | 4 | 0 | 0 | 0 | 0 |
| 332 | 4 | 0 | 0 | 0 | 0 |
| 333 | 4 | 0 | 0 | 0 | 0 |
| 334 | 4 | 0 | 0 | 0 | 0 |
| 335 | 4 | 0 | 0 | 0 | 0 |
| 336 | 4 | 0 | 0 | 0 | 0 |
| 337 | 3 | 0 | 0 | 0 | 0 |
| 338 | 3 | 0 | 0 | 0 | 0 |
| 339 | 3 | 0 | 0 | 0 | 0 |
| 340 | 3 | 0 | 0 | 0 | 0 |
| 341 | 3 | 0 | 0 | 0 | 0 |
| 342 | 3 | 0 | 0 | 0 | 0 |
| 343 | 3 | 0 | 0 | 0 | 0 |
| 344 | 3 | 0 | 0 | 0 | 0 |
| 345 | 3 | 0 | 0 | 0 | 0 |
| 346 | 3 | 0 | 0 | 0 | 0 |
| 347 | 3 | 0 | 0 | 0 | 0 |
| 348 | 3 | 0 | 0 | 0 | 0 |
| 349 | 3 | 0 | 0 | 0 | 0 |
| 350 | 3 | 0 | 0 | 0 | 0 |
| 351 | 3 | 0 | 0 | 0 | 0 |
| 352 | 3 | 0 | 0 | 0 | 0 |
| 353 | 3 | 0 | 0 | 0 | 0 |
| 354 | 3 | 0 | 0 | 0 | 0 |
| 355 | 3 | 0 | 0 | 0 | 0 |
| 356 | 3 | 0 | 0 | 0 | 0 |
| 357 | 3 | 0 | 0 | 0 | 0 |
| 358 | 3 | 0 | 0 | 0 | 0 |
| 359 | 3 | 0 | 0 | 0 | 0 |
| 360 | 3 | 0 | 0 | 0 | 0 |
| 361 | 3 | 0 | 0 | 0 | 0 |
| 362 | 3 | 0 | 0 | 0 | 0 |
| 363 | 3 | 0 | 0 | 0 | 0 |
| 364 | 3 | 0 | 0 | 0 | 0 |
| 365 | 3 | 0 | 0 | 0 | 0 |
| 366 | 3 | 0 | 0 | 0 | 0 |
| 367 | 3 | 0 | 0 | 0 | 0 |
| 368 | 3 | 0 | 0 | 0 | 0 |
| 369 | 2 | 0 | 0 | 0 | 0 |
| 370 | 2 | 0 | 0 | 0 | 0 |
| 371 | 2 | 0 | 0 | 0 | 0 |
| 372 | 2 | 0 | 0 | 0 | 0 |
| 373 | 2 | 0 | 0 | 0 | 0 |
| 374 | 2 | 0 | 0 | 0 | 0 |
| 375 | 2 | 0 | 0 | 0 | 0 |
| 376 | 2 | 0 | 0 | 0 | 0 |
| 377 | 2 | 0 | 0 | 0 | 0 |
| 378 | 2 | 0 | 0 | 0 | 0 |
| 379 | 2 | 0 | 0 | 0 | 0 |
| 380 | 2 | 0 | 0 | 0 | 0 |
| 381 | 2 | 0 | 0 | 0 | 0 |
| 382 | 2 | 0 | 0 | 0 | 0 |
| 383 | 2 | 0 | 0 | 0 | 0 |
| 384 | 2 | 0 | 0 | 0 | 0 |
| 385 | 2 | 0 | 0 | 0 | 0 |
| 386 | 2 | 0 | 0 | 0 | 0 |
| 387 | 2 | 0 | 0 | 0 | 0 |
| 388 | 2 | 0 | 0 | 0 | 0 |
| 389 | 2 | 0 | 0 | 0 | 0 |
| 390 | 2 | 0 | 0 | 0 | 0 |
| 391 | 2 | 0 | 0 | 0 | 0 |
| 392 | 2 | 0 | 0 | 0 | 0 |
| 393 | 2 | 0 | 0 | 0 | 0 |
| 394 | 2 | 0 | 0 | 0 | 0 |
| 395 | 2 | 0 | 0 | 0 | 0 |
| 396 | 2 | 0 | 0 | 0 | 0 |
| 397 | 2 | 0 | 0 | 0 | 0 |
| 398 | 2 | 0 | 0 | 0 | 0 |
| 399 | 2 | 0 | 0 | 0 | 0 |
| 400 | 2 | 0 | 0 | 0 | 0 |
| 401 | 2 | 0 | 0 | 0 | 0 |
| 402 | 2 | 0 | 0 | 0 | 0 |
| 403 | 2 | 0 | 0 | 0 | 0 |
| 404 | 2 | 0 | 0 | 0 | 0 |
| 405 | 2 | 0 | 0 | 0 | 0 |
| 406 | 2 | 0 | 0 | 0 | 0 |
| 407 | 2 | 0 | 0 | 0 | 0 |
| 408 | 2 | 0 | 0 | 0 | 0 |
| 409 | 2 | 0 | 0 | 0 | 0 |
| 410 | 2 | 0 | 0 | 0 | 0 |
| 411 | 2 | 0 | 0 | 0 | 0 |
| 412 | 2 | 0 | 0 | 0 | 0 |
| 413 | 2 | 0 | 0 | 0 | 0 |
| 414 | 2 | 0 | 0 | 0 | 0 |
| 415 | 2 | 0 | 0 | 0 | 0 |
| 416 | 2 | 0 | 0 | 0 | 0 |
| 417 | 2 | 0 | 0 | 0 | 0 |
| 418 | 2 | 0 | 0 | 0 | 0 |
| 419 | 2 | 0 | 0 | 0 | 0 |
| 420 | 2 | 0 | 0 | 0 | 0 |
| 421 | 2 | 0 | 0 | 0 | 0 |
| 422 | 2 | 0 | 0 | 0 | 0 |
| 423 | 2 | 0 | 0 | 0 | 0 |
| 424 | 2 | 0 | 0 | 0 | 0 |
| 425 | 2 | 0 | 0 | 0 | 0 |
| 426 | 2 | 0 | 0 | 0 | 0 |
| 427 | 2 | 0 | 0 | 0 | 0 |
| 428 | 2 | 0 | 0 | 0 | 0 |
| 429 | 2 | 0 | 0 | 0 | 0 |
| 430 | 2 | 0 | 0 | 0 | 0 |
| 431 | 2 | 0 | 0 | 0 | 0 |
| 432 | 2 | 0 | 0 | 0 | 0 |
| 433 | 2 | 0 | 0 | 0 | 0 |
| 434 | 2 | 0 | 0 | 0 | 0 |
| 435 | 2 | 0 | 0 | 0 | 0 |
| 436 | 2 | 0 | 0 | 0 | 0 |
| 437 | 2 | 0 | 0 | 0 | 0 |
| 438 | 2 | 0 | 0 | 0 | 0 |
| 439 | 2 | 0 | 0 | 0 | 0 |
| 440 | 2 | 0 | 0 | 0 | 0 |
| 441 | 2 | 0 | 0 | 0 | 0 |
| 442 | 2 | 0 | 0 | 0 | 0 |
| 443 | 2 | 0 | 0 | 0 | 0 |
| 444 | 2 | 0 | 0 | 0 | 0 |
| 445 | 2 | 0 | 0 | 0 | 0 |
| 446 | 2 | 0 | 0 | 0 | 0 |
| 447 | 2 | 0 | 0 | 0 | 0 |
| 448 | 2 | 0 | 0 | 0 | 0 |
| 449 | 2 | 0 | 0 | 0 | 0 |
| 450 | 2 | 0 | 0 | 0 | 0 |
| 451 | 2 | 0 | 0 | 0 | 0 |
| 452 | 2 | 0 | 0 | 0 | 0 |
| 453 | 2 | 0 | 0 | 0 | 0 |
| 454 | 2 | 0 | 0 | 0 | 0 |
| 455 | 2 | 0 | 0 | 0 | 0 |
| 456 | 2 | 0 | 0 | 0 | 0 |
| 457 | 2 | 0 | 0 | 0 | 0 |
| 458 | 2 | 0 | 0 | 0 | 0 |
| 459 | 2 | 0 | 0 | 0 | 0 |
| 460 | 2 | 0 | 0 | 0 | 0 |
| 461 | 2 | 0 | 0 | 0 | 0 |
| 462 | 2 | 0 | 0 | 0 | 0 |
| 463 | 2 | 0 | 0 | 0 | 0 |
| 464 | 1 | 0 | 0 | 0 | 0 |
| 465 | 1 | 0 | 0 | 0 | 0 |
| 466 | 1 | 0 | 0 | 0 | 0 |
| 467 | 1 | 0 | 0 | 0 | 0 |
| 468 | 1 | 0 | 0 | 0 | 0 |
| 469 | 1 | 0 | 0 | 0 | 0 |
| 470 | 1 | 0 | 0 | 0 | 0 |
| 471 | 1 | 0 | 0 | 0 | 0 |
| 472 | 1 | 0 | 0 | 0 | 0 |
| 473 | 1 | 0 | 0 | 0 | 0 |
| 474 | 1 | 0 | 0 | 0 | 0 |
| 475 | 1 | 0 | 0 | 0 | 0 |
| 476 | 1 | 0 | 0 | 0 | 0 |
| 477 | 1 | 0 | 0 | 0 | 0 |
| 478 | 1 | 0 | 0 | 0 | 0 |
| 479 | 1 | 0 | 0 | 0 | 0 |
| 480 | 1 | 0 | 0 | 0 | 0 |
| 481 | 1 | 0 | 0 | 0 | 0 |
| 482 | 1 | 0 | 0 | 0 | 0 |
| 483 | 1 | 0 | 0 | 0 | 0 |
| 484 | 1 | 0 | 0 | 0 | 0 |
| 485 | 1 | 0 | 0 | 0 | 0 |
| 486 | 1 | 0 | 0 | 0 | 0 |
| 487 | 1 | 0 | 0 | 0 | 0 |
| 488 | 1 | 0 | 0 | 0 | 0 |
| 489 | 1 | 0 | 0 | 0 | 0 |
| 490 | 1 | 0 | 0 | 0 | 0 |
| 491 | 1 | 0 | 0 | 0 | 0 |
| 492 | 1 | 0 | 0 | 0 | 0 |
| 493 | 1 | 0 | 0 | 0 | 0 |
| 494 | 1 | 0 | 0 | 0 | 0 |
| 495 | 1 | 0 | 0 | 0 | 0 |
| 496 | 1 | 0 | 0 | 0 | 0 |
| 497 | 1 | 0 | 0 | 0 | 0 |
| 498 | 1 | 0 | 0 | 0 | 0 |
Models, Graphs and Plots
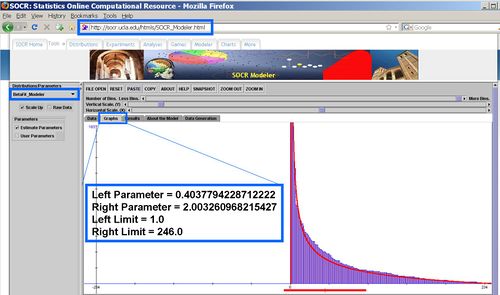
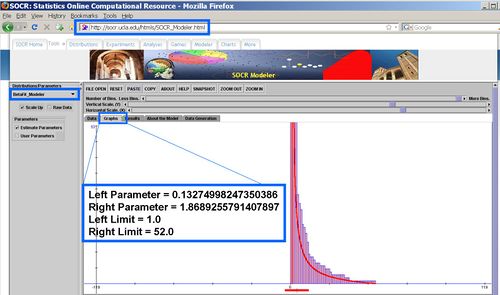
The plots below demonstrate fitting Beta-distribution models to each of the number-of-citations included in the author-columns above. These model-fits and graphs are produced by SOCR Modeler, but one may also use SOCR Charts for similar plots. The insert images within each graph show the best fit for the Beta-distribution parameters.



- SOCR Home page: http://www.socr.umich.edu
Translate this page:
