SOCR EduMaterials Activities Binomial Distributions
This is an activity to explore the Binomial, Geometric, and Hypergeometric Probability Distributions.
- Description: You can access the applets for the above distributions at http://www.socr.ucla.edu/htmls/SOCR_Distributions.html .
- Exercise 1: Use SOCR to graph and print the following distributions and answer the questions below. Also, comment on the shape of each one of these distributions:
- a. \( X \sim b(10,0.5) \), find \( P(X=3) \), \( E(X) \), \( sd(X) \), and verify them with the formulas discussed in class.
- b. \( X \sim b(10,0.1) \), find \( P(1 \le X \le 3) \).
- c. \( X \sim b(10,0.9) \), find \( P(5 < X < 8), \ P(X < 8), \ P(X \le 7), \ P(X \ge 9) \).
- d. \( X \sim b(30,0.1) \), find \( P(X > 2) \).
Below you can see a snapshot of the distribution of \( X \sim b(20,0.3) \)
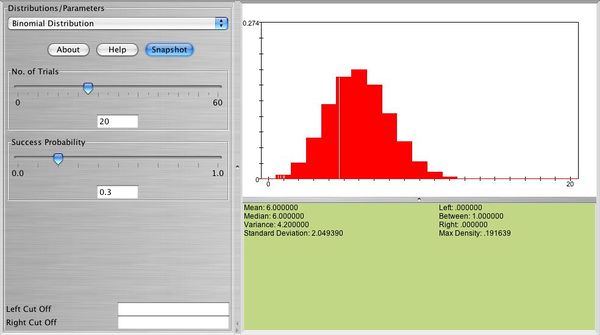
- Exercise 2: Use SOCR to graph and print the distribution of a geometric random variable with \( p=0.2, p=0.7 \). What is the shape of these distributions? What happens when \( p \) is large? What happens when \( p \) is small?
Below you can see a snapshot of the distribution of \( X \sim geometric(0.4) \)
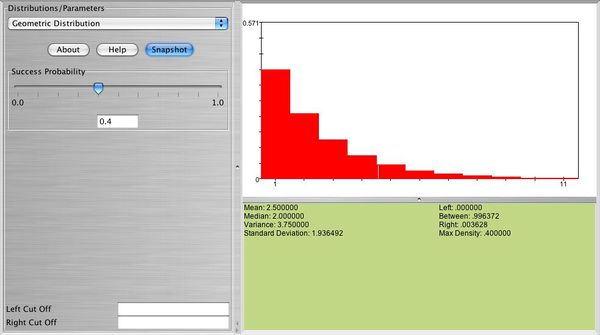
- Exercise 3: Select the geometric probability distribution with \( p=0.2 \). Use SOCR to compute the following:
- a. \( P(X=5) \)
- b. \( P(X > 3) \)
- c. \( P(X \le 5) \)
- d. \( P(X > 6) \)
- e. \( P(X \ge 8) \)
- f. \( P(4 \le X \le 9) \)
- g. \( P(4 < X < 9) \)
- Exercise 4: Verify that your answers in exercise 3 agree with the formulas discussed in class, for example, \( P(X=x)=(1-p)^{x-1}p \), \( P(X > k)=(1-p)^k \), etc. Write all your answers in detail using those formulas.
- Exercise 5: Let \( X \) follow the hypergeometric probability distribution with \( N=52 \), \( n=10 \), and number of "hot" items 13. Use SOCR to graph and print this distribution.
Below you can see a snapshot of the distribution of \( X \sim hypergeometric(N=100, n=15, r=30) \)
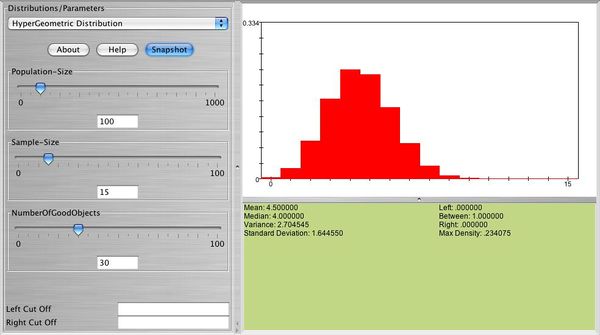
- Exercise 6: Refer to exercise 5. Use SOCR to compute \( P(X=5) \) and write down the formula that gives this answer.
- Exercise 7: Binomial approximation to hypergeometric: Let \( X \) follow the hypergeometric probability distribution with \( N=1000, \ n=10 \) and number of "hot" items 50. Graph and print this distribution.
- Exercise 8: Refer to exercise 7. Use SOCR to compute the exact probability\[ P(X=2) \]. Approximate \( P(X=2) \) using the binomial distribution. Is the approximation good? Why?
- Exercise 9: Do you think you can approximate well the hypergeometric probability distribution with \( N=50, \ n=20 \), and number of "hot" items 40 using the binomial probability distribution? Graph and print the exact (hypergeometric) and the approximate (binomial) distributions and compare.
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: