SOCR EduMaterials Activities Distributions

SOCR Educational Materials - Activities - SOCR Computing Probabilities Activity

Using SOCR to compute probabilities or critical values for different distributions
Observe the shape of the distributions by varying their parameters
Explore relations among various distributions (e.g. Poisson-binomial, binomial-hypergeometric, normal-binomial, normal-Poisson)

To go to the SOCR applet enter this URL in your browser's address field: http://www.SOCR.ucla.edu/htmls/SOCR_Distributions.html

Here we use Normal distribution (mean=5, sigma=4) as an example

Step 1: Set up parameters! Select the Normal Distribution from the drop-down list on the top-left. Set Mean = 5 & Standard Deviation = 4. Now the density function of Normal(μ=5, σ=4) will show up in the top-right with red color. See following figure.

Step 2: Compute P(X<7)! Move cursor from 21, the most right side, to the right until 7. Now the red area means X<7. And the probability of red area is always represented by the value of “Between”. Hence P(X<7)=0.691431. See figure below.

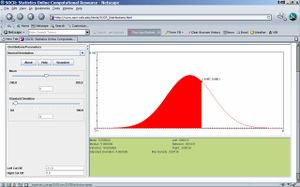
Notes: To get a snapshot of this result, click on Snapshot. Then save the file with a filename and extension .jpg , for example, HW1_Image2.jpg. When done, you can open that new .jpeg file and go to edit→copy. Open separately a Word file and paste into that file. You can reduce the image, but make sure that it is big enough for us to see the numbers.

Step 3: Compute P(X>3)! Move cursor from -11, the most right side, to the left until 3. Red area means X>3. And the probability of red area is always recorded in the value of “Between”. Therefore, P(X>3)=0.691431. See figure below. The same result can be obtained by using the Left Cut-Off and Right Cut-Off boxes on the bottom-left corner of the applet. Is the result the same as in Step 2, by chance? Explain!

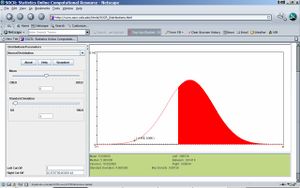
Step 4: Compute P(2<X<6)! First, move cursor from -11, the most left side, to the right until 2. Then move cursor from 21, the most right side, to the left until 6. Find “Between” in the bottom-right widow, which is just the probability of red area. Then P(2<X<6)=0.372079. See attached figure.

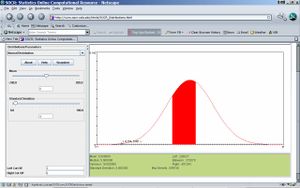
Notes: Similarly, we can use SOCR to compute the probability in other known distribution, such as uniform distribution, exponential distribution, beta distribution, etc.

Step 5: Now find the critical value d, so that P(X<d)=0.456; d also represents the 45.6^th percentile of the N(μ=5, σ=4) distribution! Move the left vertical limit on the graph to the left (close to -11). Start the right limit from 11 and move it down until you reach 4.55849, monitor the “between” red area and it’s probability value (0.456). You may also experiment with setting the limits numerically using the Left and Right Cut-Off text-fields on the bottom-left of the applet. These allow more accurate vertical limit setting.

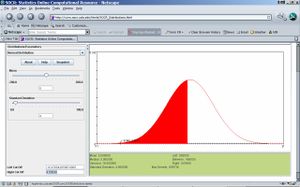
Questions
- What is the area bound below the Normal density curve on the interval [μ-2σ, μ+2σ]? Does it depend on the values of μ & σ?
- What is the critical value to, that gives P(t>t_o)=0.025, when t~T_df=15?
- Which one is larger t_o or t₁, where P(T_o > t_o)=P(T₁ > t₁)=0.025, and T_o ~ T_df=15, T₁ ~ T_df=5? What is the limit of t_o as df--> ∞?

Translate this page:

(default)	Deutsch	Español	Français	Italiano	Português	日本語	България	الامارات العربية المتحدة	Suomi	इस भाषा में	Norge
한국어	中文	繁体中文	Русский	Nederlands	Ελληνικά	Hrvatska	Česká republika	Danmark	Polska	România	Sverige