AP Statistics Curriculum 2007 Exponential

Exponential Distribution

Definition: Exponential distribution is a special case of the gamma distribution. Whereas the gamma distribution is the waiting time for more than one event, the exponential distribution describes the time between a single Poisson event.

Probability density function: For \(X\sim Exponential(\lambda)\!\), the exponential probability density function is given by

\[\lambda e^{-\lambda x}\!\]

where

• e is the natural number (e = 2.71828…)
• \(\lambda\) is the mean time between events
• x is a random variable

Cumulative density function: The exponential cumulative distribution function is given by

\[1-e^{-\lambda x}\!\]

where

• e is the natural number (e = 2.71828…)
• \(\lambda\) is the mean time between events
• x is a random variable

Moment generating function: The exponential moment-generating function is

\[M(t)=(1-\frac{t}{\lambda})^{-1}\]

Expectation: The expected value of a exponential distributed random variable x is

\[E(X)=\frac{1}{\lambda}\]

Variance: The exponential variance is

\[Var(X)=\frac{1}{\lambda^2}\]

Applications

The exponential distribution occurs naturally when describing the waiting time in a homogeneous Poisson process. It can be used in a range of disciplines including queuing theory, physics, reliability theory, and hydrology. Examples of events that may be modeled by exponential distribution include:

• The time until a radioactive particle decays
• The time between clicks of a Geiger counter
• The time until default on payment to company debt holders
• The distance between roadkills on a given road
• The distance between mutations on a DNA strand
• The time it takes for a bank teller to serve a customer
• The height of various molecules in a gas at a fixed temperature and pressure in a uniform gravitational field
• The monthly and annual maximum values of daily rainfall and river discharge volumes

Example

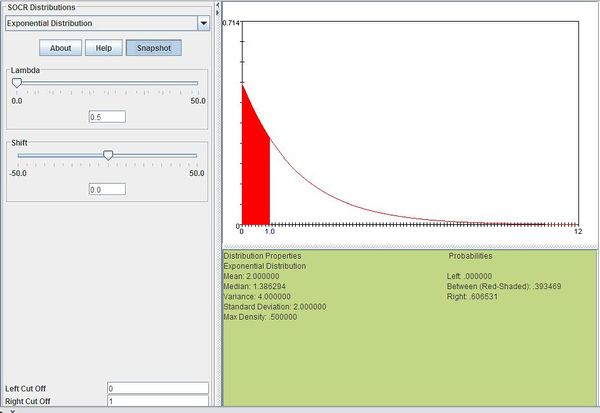
Suppose you usually get 2 phone calls per hour. Compute the probability that a phone call will arrive within the next hour.

2 phone calls per hour means that we would expect one phone call every 1/2 hour so \(\lambda=0.5\). We can then compute this as follows:

\[P(0\le X\le 1)=\sum_{x=0}^1 0.5e^{-0.5x}=0.393469\]

The figure below shows this result using SOCR distributions