Difference between revisions of "SOCR EduMaterials AnalysisActivities KruskalWallis"
(→SOCR Analyses Example on the Kruskal-Wallis Test) |
(→Result Interpretation) |
||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | == | + | ==[[SOCR_EduMaterials_AnalysesActivities | SOCR Analysis]] - Kruskal-Wallis Test Background== |
| − | + | The [[AP_Statistics_Curriculum_2007_NonParam_ANOVA | Kruskal-Wallis Test is a generalization of the Two Independent Sample Wilcoxon Test]]. While the latter one test for two groups, the Kruskal-Wallis Test test multiple groups. Suppose there are k groups, the hypotheses are written as: | |
| − | The Kruskal-Wallis Test is a generalization of the Two Independent Sample Wilcoxon Test. While the latter one test for two groups, the Kruskal-Wallis Test test multiple groups. Suppose there are k groups, the hypotheses are written as: | ||
'''Null Hypothesis H_0''': All of the k population distribution functions are identical. | '''Null Hypothesis H_0''': All of the k population distribution functions are identical. | ||
| Line 10: | Line 9: | ||
or | or | ||
| − | '''Alternative Hypothesis H_A''': The k | + | '''Alternative Hypothesis H_A''': The k populations do not all have identical means. (k is the number of groups here.) |
| − | |||
| − | |||
| − | + | Rank sum is employed for hypotheses testing. Note that the sample size for each group do not have to be the same. Go to the [http://www.socr.ucla.edu/htmls/ana/TwoIndependentKruskalWallis_Analysis.html Kruskal-Wallis Test Applet]. | |
| + | ==SOCR Analyses Example on the Kruskal-Wallis Test== | ||
The example we show here is from "Practical Nonparametric Statistics" by Conover, Second Edition, John Wiley & Sons, 1980. (Page 230) | The example we show here is from "Practical Nonparametric Statistics" by Conover, Second Edition, John Wiley & Sons, 1980. (Page 230) | ||
| − | '''Steps:''' | + | =='''Steps:'''== |
| − | + | === The data of this example has 4 groups: A, B, C and D. Click on "'''Kruskal-Wallis Test'''" from the conbo box in the left panel=== | |
| Line 31: | Line 29: | ||
| − | + | ===Click on "'''Example 2'''" button. than the "Data" button to see the data=== | |
<center>[[Image:SOCR_AnalysisActivities_KruskalWallies_Chu_061407_Fig2.gif|700px]]</center> | <center>[[Image:SOCR_AnalysisActivities_KruskalWallies_Chu_061407_Fig2.gif|700px]]</center> | ||
| − | + | === The data need to be send to the computer for analysis=== | |
| + | In the Kruskal-Wallis test, at least two groups need to be included. You can certainly include any two groups, any three groups, or all the available groups, etc., from the data set. The test will only analyze the groups selected. Therefore, you'll need to let the computer know what groups you're choosing. This is done in the "Mapping" panel. Click on the "Mapping" button to include the groups you want. | ||
<center>[[Image:SOCR_AnalysisActivities_KruskalWallies_Chu_061407_Fig2A.gif|700px]]</center> | <center>[[Image:SOCR_AnalysisActivities_KruskalWallies_Chu_061407_Fig2A.gif|700px]]</center> | ||
| − | + | === Next, click on the "'''Calculate'''" button=== | |
| − | + | Now you're ready to see the results. Just click on the "Result" button. | |
<center>[[Image:SOCR_AnalysisActivities_KruskalWallies_Chu_061407_Fig3.gif|700px]]</center> | <center>[[Image:SOCR_AnalysisActivities_KruskalWallies_Chu_061407_Fig3.gif|700px]]</center> | ||
| Line 50: | Line 49: | ||
| − | '''Note''': if you happen to click on the "Clear" button in the middle of the procedure, all the data will be cleared out. Simply start over from step 1 and | + | '''Note''': if you happen to click on the "Clear" button in the middle of the procedure, all the data will be cleared out. Simply start over from step 1 and retrieve the data by click an '''EXAMPLE''' button. |
| − | + | ===Result Interpretation=== | |
* The '''Results''' tab ends with a summary like this: | * The '''Results''' tab ends with a summary like this: | ||
::Significance Level = 0.05<br> | ::Significance Level = 0.05<br> | ||
| Line 60: | Line 59: | ||
::S * S = 34.632<br> | ::S * S = 34.632<br> | ||
<br> | <br> | ||
| − | The test statistic that follows Student's t-distribution is: | + | The test statistic that follows Student's t-distribution is:<br> |
| − | |Ri/ni - Rj/nj| / (S * S * (N - 1 - T) / (N - k)) / sqrt(1/ni + 1/nj) | + | ::|Ri/ni - Rj/nj| / sqrt(S * S * (N - 1 - T) / (N - k)) / sqrt(1/ni + 1/nj) (or identically) |
| + | :: $$\sqrt{{1\over n_i} + {1\over n_j}}\times {|{R_i\over n_i} - {R_j\over n_j}| \over ({S^2 (N - 1 - T) \over N - k})^{0.5}}$$ | ||
| + | |||
It is computed using T and S above. N is the total number of observations. | It is computed using T and S above. N is the total number of observations. | ||
<br><br> | <br><br> | ||
| Line 68: | Line 69: | ||
:::: |Ri/ni - Rj/nj| 2.1199 * sqrt(24.9187) * sqrt(1/ni + 1/nj)<br> | :::: |Ri/ni - Rj/nj| 2.1199 * sqrt(24.9187) * sqrt(1/ni + 1/nj)<br> | ||
<br> | <br> | ||
| − | ::Group A vs. Group B: 3.1999 < 6.6928 (does not yield rejection of Ho | + | ::Group A vs. Group B: 3.1999 < 6.6928 (does not yield rejection of Ho) |
| − | ::Group A vs. Group C: 4.7000 < 6.6928 (does not yield rejection of Ho | + | ::Group A vs. Group C: 4.7000 < 6.6928 (does not yield rejection of Ho) |
| − | ::Group A vs. Group D: 5.7000 < 6.6928 (does not yield rejection of Ho | + | ::Group A vs. Group D: 5.7000 < 6.6928 (does not yield rejection of Ho) |
| − | ::Group B vs. Group C: 7.9 > 6.6928 (yields rejection of Ho | + | ::'''Group B vs. Group C: 7.9 > 6.6928 (yields rejection of Ho)''' |
| − | ::Group B vs. Group D: 8.9 > 6.6928 (yields rejection of Ho | + | ::'''Group B vs. Group D: 8.9 > 6.6928 (yields rejection of Ho)''' |
| − | ::Group C vs. Group D: 1.0 < 6.6928 (does not yield rejection of Ho | + | ::Group C vs. Group D: 1.0 < 6.6928 (does not yield rejection of Ho) |
Since Group B appears to have different mean ranks than group C and group D, the null hypothesis is rejected. | Since Group B appears to have different mean ranks than group C and group D, the null hypothesis is rejected. | ||
| − | * These | + | * These results include the critical value (2.120) and the value of the test statistics (''T=7.487''), which indicate that there is sufficient evidence (at <math>\alpha=0.05</math>) to reject the null hypothesis that the sample centers are equal. |
* Also, the paired-group comparisons (accounting for multiple-testing) indicate the ''normal'' ranges of the rank differences between groups. For instance, ''Group B vs. Group C: 7.9 > 6.6928'' indicates the range of normal rank differences between groups ''B'' and ''C''. | * Also, the paired-group comparisons (accounting for multiple-testing) indicate the ''normal'' ranges of the rank differences between groups. For instance, ''Group B vs. Group C: 7.9 > 6.6928'' indicates the range of normal rank differences between groups ''B'' and ''C''. | ||
Latest revision as of 17:53, 5 September 2014
Contents
[hide]- 1 SOCR Analysis - Kruskal-Wallis Test Background
- 2 SOCR Analyses Example on the Kruskal-Wallis Test
- 3 Steps:
- 3.1 The data of this example has 4 groups: A, B, C and D. Click on "Kruskal-Wallis Test" from the conbo box in the left panel
- 3.2 Click on "Example 2" button. than the "Data" button to see the data
- 3.3 The data need to be send to the computer for analysis
- 3.4 Next, click on the "Calculate" button
- 3.5 Result Interpretation
- 4 References
SOCR Analysis - Kruskal-Wallis Test Background
The Kruskal-Wallis Test is a generalization of the Two Independent Sample Wilcoxon Test. While the latter one test for two groups, the Kruskal-Wallis Test test multiple groups. Suppose there are k groups, the hypotheses are written as:
Null Hypothesis H_0: All of the k population distribution functions are identical.
Alternative Hypothesis H_A: At least one of the populations tends to yield larger observations than at least one of the other populations.
or
Alternative Hypothesis H_A: The k populations do not all have identical means. (k is the number of groups here.)
Rank sum is employed for hypotheses testing. Note that the sample size for each group do not have to be the same. Go to the Kruskal-Wallis Test Applet.
SOCR Analyses Example on the Kruskal-Wallis Test
The example we show here is from "Practical Nonparametric Statistics" by Conover, Second Edition, John Wiley & Sons, 1980. (Page 230)
Steps:
The data of this example has 4 groups: A, B, C and D. Click on "Kruskal-Wallis Test" from the conbo box in the left panel

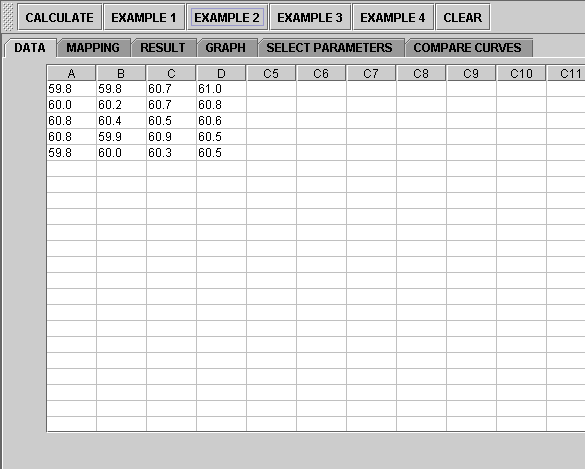
Click on "Example 2" button. than the "Data" button to see the data
The data need to be send to the computer for analysis
In the Kruskal-Wallis test, at least two groups need to be included. You can certainly include any two groups, any three groups, or all the available groups, etc., from the data set. The test will only analyze the groups selected. Therefore, you'll need to let the computer know what groups you're choosing. This is done in the "Mapping" panel. Click on the "Mapping" button to include the groups you want.

Next, click on the "Calculate" button
Now you're ready to see the results. Just click on the "Result" button.

Scroll down to see complete results.
If you'd like to include some other group(s) or remove the current groups and start over, simply go to the Mapping button and take the groups you want.
Note: if you happen to click on the "Clear" button in the middle of the procedure, all the data will be cleared out. Simply start over from step 1 and retrieve the data by click an EXAMPLE button.
Result Interpretation
- The Results tab ends with a summary like this:
- Significance Level = 0.05
- Degrees of Freedom = 16
- Critical Value = 2.120
- Test Statistic T = 7.487
- S * S = 34.632
- Significance Level = 0.05
The test statistic that follows Student's t-distribution is:
- |Ri/ni - Rj/nj| / sqrt(S * S * (N - 1 - T) / (N - k)) / sqrt(1/ni + 1/nj) (or identically)
- $$\sqrt{{1\over n_i} + {1\over n_j}}\times {|{R_i\over n_i} - {R_j\over n_j}| \over ({S^2 (N - 1 - T) \over N - k})^{0.5}}$$
It is computed using T and S above. N is the total number of observations.
- Notation: Ri -- Sum of ranks of group i; ni -- size of group i.
- Notation: Ri -- Sum of ranks of group i; ni -- size of group i.
- |Ri/ni - Rj/nj| 2.1199 * sqrt(24.9187) * sqrt(1/ni + 1/nj)
- |Ri/ni - Rj/nj| 2.1199 * sqrt(24.9187) * sqrt(1/ni + 1/nj)
- Group A vs. Group B: 3.1999 < 6.6928 (does not yield rejection of Ho)
- Group A vs. Group C: 4.7000 < 6.6928 (does not yield rejection of Ho)
- Group A vs. Group D: 5.7000 < 6.6928 (does not yield rejection of Ho)
- Group B vs. Group C: 7.9 > 6.6928 (yields rejection of Ho)
- Group B vs. Group D: 8.9 > 6.6928 (yields rejection of Ho)
- Group C vs. Group D: 1.0 < 6.6928 (does not yield rejection of Ho)
Since Group B appears to have different mean ranks than group C and group D, the null hypothesis is rejected.
- These results include the critical value (2.120) and the value of the test statistics (T=7.487), which indicate that there is sufficient evidence (at \(\alpha=0.05\)) to reject the null hypothesis that the sample centers are equal.
- Also, the paired-group comparisons (accounting for multiple-testing) indicate the normal ranges of the rank differences between groups. For instance, Group B vs. Group C: 7.9 > 6.6928 indicates the range of normal rank differences between groups B and C.
References
- Conover, WJ (1980). Practical Nonparametric Statistics. John Wiley & Sons. Second Edition.
Translate this page: