Difference between revisions of "SOCR EduMaterials Activities Discrete Distributions"

From SOCR
Jump to: navigation, search
 
m
 
(42 intermediate revisions by 2 users not shown)
Line 1: Line 1:
 +
== This is an activity to explore the Normal Probability Distribution and the normal approximation to binomial. ==
  
−
\item[a.]  Use $SOCR$ to graph and print the following distributions and answer the questions below.  Also, comment on the shape of each one of these distributions:  \\
+
* '''Description''':  You can access the applets for the above distributions at  http://www.socr.ucla.edu/htmls/SOCR_Distributions.html .  
−
$X \sim b(10,0.5)$, find $P(X=3), E(X), sd(X)$, and verify them with the formulas. \\
+
 
−
$X \sim b(10,0.1)$, find $P(1 \le X \le 3)$.  \\
+
*'''Exercise 1:''' Use SOCR to graph and print the distribution of <math> X \sim N(20, 3) </math>.  Show on the graph the following points: <math>\mu \pm 1 \sigma, \mu \pm 2 \sigma, \mu \pm 3 \sigma </math>. How many standard deviations from the mean is the value <math> x=27.5 </math>?
−
$X \sim b(10,0.9)$, find $P(5 < X < 8), P(X < 8), P(X \le 7), P(X \ge 9)$.  \\
+
*'''Exercise 2:''' Graph the distribution of <math> X \sim N(40, 10)</math>.  
−
$X \sim b(30,0.1)$, find $P(X > 2)$.
+
**'''1.''' Find <math>P(X>49) </math>  Submit a printout.
−
%Below you can see the distribution of <math> X \sim b(20,0.3) <\math>
+
**'''2.''' Find <math>P(X<22) </math> Submit a printout.
−
\item[b.]  Use $SOCR$ to graph and print the distribution of a geometric random variable with $p=0.2,  p=0.7$.  What is the shape of these distributions?  What happens when $p$ is large?  What happens when $p$ is small?
+
**'''3.''' Find <math>P(X<58) </math>  Submit a printout.
−
%Below you can see the distribution of <math> X \sim geometric(0.4) <\math>
+
**'''4.''' Find <math>P(X>13) </math>  Submit a printout.
−
\item[c.]  Select the geometric probability distribution with $p=0.2$.  Use $SOCR$ to compute the following:
+
**'''5.''' Find <math>P(12<X<37) </math>  Submit a printout.
−
\begin{itemize}
+
**'''6.''' Find <math>P(33<X<60) </math>  Submit a printout.
−
\item[1.] $P(X=5)$
+
**'''7.''' Find <math>P(52<X<65) </math>  Submit a printout.
−
\item[2.] $P(X > 3)$
+
**'''8.''' Use the mouse or the left cut off or right cut off points to find the <math>8^{th}, 20^{th}, 45^{th}, 55^{th}, 70^{th}, 95^{th}</math> percentiles.  After you find these percentiles you can place by hand all of them in one printout (or you can submit a printout for each one of them if you want).
−
\item[3.] $P(X \le 5)$
+
**'''9.''' Make sure you know how to answer the above questions using the <math>z</math> score <math>z=\frac{x-\mu}{\sigma}</math> and your <math>z</math> table from the handout! You do not need to submit anything here.
−
\item[4.]  $P(X > 6)$
+
**'''10.'''  The lifetime of tires of brand <math>A</math> follows the normal distribution with mean 40000 miles and standard deviation 4000 miles.   
−
\item[5.]  $P(X \ge 8)$
+
 
−
\item[6.]  $P(4 \le X \le 9)$
+
**'''1.''' Use <math>SOCR</math> to find the probability that a tire will last between 40000 and 46000 miles.
−
\item[7.]  $P(4 < X < 9)$
+
**'''2.''' Given that a tire will last more than 46000 miles what is the probability that it will last more than 50000 miles?  Submit a printout and explain how you get the answer.
−
\end{itemize}
+
**'''3.''' Given that a tire will last more than 46000 miles what is the probability that it will last less than 50000 miles?  Submit a printout and explain how you get the answer.
−
\item[d.] Verify that your answers in part (c) agree with the formulas we discussed in class, for example, $P(X=x)=(1-p)^{x-1}p$, $P(X > k)=(1-p)^k$, etc.  Write all your answers in detail using those formulas.
 
−
\item[e.] Let $X$ follow the hypergeometric probability distribution with $N=52$, $n=10$, and number of ``hot" items 13. Use $SOCR$ to graph and print this distribution.
 
−
%Below you can see the distribution of <math> X \sim hypergeometric(N=100, n=15, r=30) <\math>
 
−
\item[f.] Refer to part (e).  Use $SOCR$ to compute $P(X=5)$ and write down the formula that gives this answer.
 
−
\item[g.] Binomial approximation to hypergeometric: \\
 
−
Let $X$ follow the hypergeometric probability distribution with $N=1000, n=10$ and number of ``hot" items 50.  Graph and print this distribution.
 
−
\item[h.] Refer to part (g).  Use $SOCR$ to compute the exact probability: $P(X=2)$. Approximate $P(X=2)$ using binomial distribution. Is the approximation good?  Why?
 
−
\item[i.]  Do you think you can approximate well the hypergeometric probability distribution with $N=50, n=10$, and number of ``hot" items 40 using the binomial probability distribution?  Explain.
 
 
\end{itemize}
 
\end{itemize}
 +
**'''4.'''  The probability that a student is admitted in the Math Department Major at a college is <math>30 \%</math>.  Suppose that this year 150 students will apply for admission into the Math major. 
 +
**'''5.'''  What is the distribution of the number of students admitted?  Use <math>SOCR</math> to graph and print this distribution.  What is the shape of this distribution?  What is the mean and standard deviation of this distribution?
 +
**'''6.'''  Write an expression for the exact probability that among the 150 students at least 55 will be admitted.
 +
**'''7.'''  Use [[SOCR]] to compute the probability of part (2).
 +
**'''8.'''  Use the normal distribution to approximate the probability of part (2) (do not forget the continuity correction).  What is the error of the approximation?
 +
 +
 +
 +
  
 +
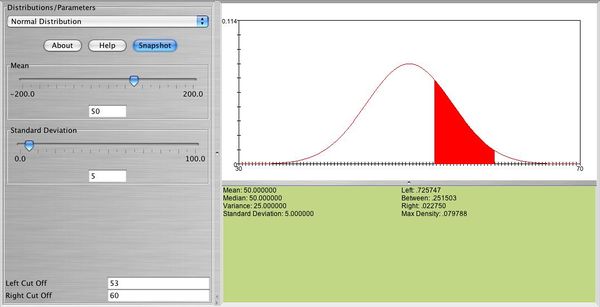
Below you can see the distribution of a normal random variable <math> X </math> with <math> \mu=50, \sigma=5 </math>.  In this graph you can also see the probability that <math> X </math> is between 53 and 60.
  
  
 +
<center>[[Image: SOCR_Activities_Christou_normal.jpg|600px]]</center>
  
  
Line 37: Line 41:
 
* SOCR Home page: http://www.socr.ucla.edu
 
* SOCR Home page: http://www.socr.ucla.edu
  
−
{{translate|pageName=http://wiki.stat.ucla.edu/socr/index.php?title=SOCR_EduMaterials_Activities_ConfidenceIntervals}}</math>
+
{{translate|pageName=http://wiki.stat.ucla.edu/socr/index.php?title=SOCR_EduMaterials_Activities_Discrete_Distributions}}
 +
 
 +
</math>

Latest revision as of 12:27, 12 June 2007

This is an activity to explore the Normal Probability Distribution and the normal approximation to binomial.

  • Exercise 1: Use SOCR to graph and print the distribution of \( X \sim N(20, 3) \). Show on the graph the following points\[\mu \pm 1 \sigma, \mu \pm 2 \sigma, \mu \pm 3 \sigma \]. How many standard deviations from the mean is the value \( x=27.5 \)?
  • Exercise 2: Graph the distribution of \( X \sim N(40, 10)\).
    • 1. Find \(P(X>49) \) Submit a printout.
    • 2. Find \(P(X<22) \) Submit a printout.
    • 3. Find \(P(X<58) \) Submit a printout.
    • 4. Find \(P(X>13) \) Submit a printout.
    • 5. Find \(P(12<X<37) \) Submit a printout.
    • 6. Find \(P(33<X<60) \) Submit a printout.
    • 7. Find \(P(52<X<65) \) Submit a printout.
    • 8. Use the mouse or the left cut off or right cut off points to find the \(8^{th}, 20^{th}, 45^{th}, 55^{th}, 70^{th}, 95^{th}\) percentiles. After you find these percentiles you can place by hand all of them in one printout (or you can submit a printout for each one of them if you want).
    • 9. Make sure you know how to answer the above questions using the \(z\) score \(z=\frac{x-\mu}{\sigma}\) and your \(z\) table from the handout! You do not need to submit anything here.
    • 10. The lifetime of tires of brand \(A\) follows the normal distribution with mean 40000 miles and standard deviation 4000 miles.
    • 1. Use \(SOCR\) to find the probability that a tire will last between 40000 and 46000 miles.
    • 2. Given that a tire will last more than 46000 miles what is the probability that it will last more than 50000 miles? Submit a printout and explain how you get the answer.
    • 3. Given that a tire will last more than 46000 miles what is the probability that it will last less than 50000 miles? Submit a printout and explain how you get the answer.

\end{itemize}

    • 4. The probability that a student is admitted in the Math Department Major at a college is \(30 \%\). Suppose that this year 150 students will apply for admission into the Math major.
    • 5. What is the distribution of the number of students admitted? Use \(SOCR\) to graph and print this distribution. What is the shape of this distribution? What is the mean and standard deviation of this distribution?
    • 6. Write an expression for the exact probability that among the 150 students at least 55 will be admitted.
    • 7. Use SOCR to compute the probability of part (2).
    • 8. Use the normal distribution to approximate the probability of part (2) (do not forget the continuity correction). What is the error of the approximation?



Below you can see the distribution of a normal random variable \( X \) with \( \mu=50, \sigma=5 \). In this graph you can also see the probability that \( X \) is between 53 and 60.


SOCR Activities Christou normal.jpg



Translate this page:

(default)
Uk flag.gif

Deutsch
De flag.gif

Español
Es flag.gif

Français
Fr flag.gif

Italiano
It flag.gif

Português
Pt flag.gif

日本語
Jp flag.gif

България
Bg flag.gif

الامارات العربية المتحدة
Ae flag.gif

Suomi
Fi flag.gif

इस भाषा में
In flag.gif

Norge
No flag.png

한국어
Kr flag.gif

中文
Cn flag.gif

繁体中文
Cn flag.gif

Русский
Ru flag.gif

Nederlands
Nl flag.gif

Ελληνικά
Gr flag.gif

Hrvatska
Hr flag.gif

Česká republika
Cz flag.gif

Danmark
Dk flag.gif

Polska
Pl flag.png

România
Ro flag.png

Sverige
Se flag.gif

</math>

Retrieved from "https://wiki.socr.umich.edu/index.php?title=SOCR_EduMaterials_Activities_Discrete_Distributions&oldid=3926"