Difference between revisions of "SOCR EduMaterials Activities Distributions"
m (Reverted edit of MkiZpi, changed back to last version by IvoDinov) |
|||
| (18 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
== [[SOCR_EduMaterials_Activities | SOCR Educational Materials - Activities ]] - SOCR Computing Probabilities Activity == | == [[SOCR_EduMaterials_Activities | SOCR Educational Materials - Activities ]] - SOCR Computing Probabilities Activity == | ||
| − | + | == Goals == | |
| + | * Using SOCR to compute probabilities or critical values for different distributions | ||
| + | * Observe the shape of the distributions by varying their parameters | ||
| + | * [[SOCR_EduMaterials_Activities_Explore_Distributions | Explore relations among various distributions]] (e.g. Poisson-binomial, binomial-hypergeometric, normal-binomial, normal-Poisson) | ||
| − | + | == Applet == | |
| + | To go to the [[SOCR]] applet enter this URL in your browser's address field: http://www.SOCR.ucla.edu/htmls/SOCR_Distributions.html | ||
| − | + | == Activities== | |
| + | Here we use Normal distribution (mean=5, sigma=4) as an example | ||
| − | Step 1: Set up parameters | + | * '''Step 1''': Set up parameters! Select the Normal Distribution from the drop-down list on the top-left. Set Mean = 5 & Standard Deviation = 4. Now the density function of Normal(μ=5, σ=4) will show up in the top-right with red color. See following figure. |
| − | Select the Normal Distribution from the drop-down list on the top-left. Set | + | <center>[[Image:Dinov_SOCR_DistributionActivity_Fig1_091806.jpg|300px]]</center> |
| − | Mean = 5 | ||
| − | Standard Deviation = 4 | ||
| − | |||
| + | * '''Step 2''': Compute P(X<7)! Move cursor from 21, the most right side, to the right until 7. Now the red area means X<7. And the probability of red area is always represented by the value of “Between”. Hence P(X<7)=0.691431. See figure below. | ||
| + | <center>[[Image:Dinov_SOCR_DistributionActivity_Fig2_091806.jpg|300px]]</center> | ||
| + | * ''Notes'': To get a snapshot of this result, click on '''Snapshot'''. Then save the file with a filename and extension .jpg , for example, HW1_Image2.jpg. When done, you can open that new .jpeg file and go to edit→copy. Open separately a Word file and paste into that file. You can reduce the image, but make sure that it is big enough for us to see the numbers. | ||
| − | Step | + | * '''Step 3''': Compute P(X>3)! Move cursor from -11, the most right side, to the left until 3. Red area means X>3. And the probability of red area is always recorded in the value of “Between”. Therefore, P(X>3)=0.691431. See figure below. The same result can be obtained by using the Left Cut-Off and Right Cut-Off boxes on the bottom-left corner of the applet. Is the result the same as in Step 2, by chance? Explain! |
| − | + | <center>[[Image:Dinov_SOCR_DistributionActivity_Fig3_091806.jpg|300px]]</center> | |
| − | + | * '''Step 4''': Compute P(2<X<6)! First, move cursor from -11, the most left side, to the right until 2. Then move cursor from 21, the most right side, to the left until 6. Find “Between” in the bottom-right widow, which is just the probability of red area. Then P(2<X<6)=0.372079. See attached figure. | |
| + | <center>[[Image:Dinov_SOCR_DistributionActivity_Fig4_091806.jpg|300px]]</center> | ||
| + | * ''Notes'': Similarly, we can use SOCR to compute the probability in other known distribution, such as uniform distribution, exponential distribution, beta distribution, etc. | ||
| − | Step | + | * '''Step 5''': Now find the critical value d, so that P(X<d)=0.456; d also represents the 45.6<sup>th</sup> percentile of the N(μ=5, σ=4) distribution! Move the left vertical limit on the graph to the left (close to -11). Start the right limit from 11 and move it down until you reach 4.55849, monitor the “between” red area and it’s probability value (0.456). You may also experiment with setting the limits numerically using the Left and Right Cut-Off text-fields on the bottom-left of the applet. These allow more accurate vertical limit setting. |
| − | + | <center>[[Image:Dinov_SOCR_DistributionActivity_Fig5_091806.jpg|300px]]</center> | |
| − | + | * '''Questions''' | |
| − | + | **What is the area bound below the Normal density curve on the interval ''[μ-2σ, μ+2σ]''? Does it depend on the values of ''μ'' & ''σ''? | |
| + | ** What is the critical value to, that gives P(t>t<sub>o</sub>)=0.025, when t~T<sub>df=15</sub>? | ||
| + | ** Which one is larger t<sub>o</sub> or t<sub>1</sub>, where P(T<sub>o</sub> > t<sub>o</sub>)=P(T<sub>1</sub> > t<sub>1</sub>)=0.025, and T<sub>o</sub> ~ T<sub>df=15</sub>, T<sub>1</sub> ~ T<sub>df=5</sub>? What is the limit of t<sub>o</sub> as df--> ∞? | ||
| − | |||
| + | <hr> | ||
* SOCR Home page: http://www.socr.ucla.edu | * SOCR Home page: http://www.socr.ucla.edu | ||
| + | |||
| + | {{translate|pageName=http://wiki.stat.ucla.edu/socr/index.php?title=SOCR_EduMaterials_Activities_Distributions}} | ||
Latest revision as of 14:22, 10 July 2007
Contents
[hide]SOCR Educational Materials - Activities - SOCR Computing Probabilities Activity
Goals
- Using SOCR to compute probabilities or critical values for different distributions
- Observe the shape of the distributions by varying their parameters
- Explore relations among various distributions (e.g. Poisson-binomial, binomial-hypergeometric, normal-binomial, normal-Poisson)
Applet
To go to the SOCR applet enter this URL in your browser's address field: http://www.SOCR.ucla.edu/htmls/SOCR_Distributions.html
Activities
Here we use Normal distribution (mean=5, sigma=4) as an example
- Step 1: Set up parameters! Select the Normal Distribution from the drop-down list on the top-left. Set Mean = 5 & Standard Deviation = 4. Now the density function of Normal(μ=5, σ=4) will show up in the top-right with red color. See following figure.

- Step 2: Compute P(X<7)! Move cursor from 21, the most right side, to the right until 7. Now the red area means X<7. And the probability of red area is always represented by the value of “Between”. Hence P(X<7)=0.691431. See figure below.
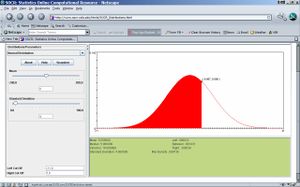
- Notes: To get a snapshot of this result, click on Snapshot. Then save the file with a filename and extension .jpg , for example, HW1_Image2.jpg. When done, you can open that new .jpeg file and go to edit→copy. Open separately a Word file and paste into that file. You can reduce the image, but make sure that it is big enough for us to see the numbers.
- Step 3: Compute P(X>3)! Move cursor from -11, the most right side, to the left until 3. Red area means X>3. And the probability of red area is always recorded in the value of “Between”. Therefore, P(X>3)=0.691431. See figure below. The same result can be obtained by using the Left Cut-Off and Right Cut-Off boxes on the bottom-left corner of the applet. Is the result the same as in Step 2, by chance? Explain!
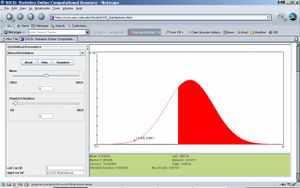
- Step 4: Compute P(2<X<6)! First, move cursor from -11, the most left side, to the right until 2. Then move cursor from 21, the most right side, to the left until 6. Find “Between” in the bottom-right widow, which is just the probability of red area. Then P(2<X<6)=0.372079. See attached figure.
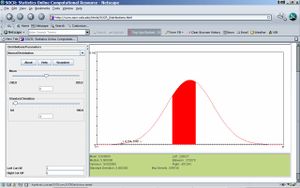
- Notes: Similarly, we can use SOCR to compute the probability in other known distribution, such as uniform distribution, exponential distribution, beta distribution, etc.
- Step 5: Now find the critical value d, so that P(X<d)=0.456; d also represents the 45.6th percentile of the N(μ=5, σ=4) distribution! Move the left vertical limit on the graph to the left (close to -11). Start the right limit from 11 and move it down until you reach 4.55849, monitor the “between” red area and it’s probability value (0.456). You may also experiment with setting the limits numerically using the Left and Right Cut-Off text-fields on the bottom-left of the applet. These allow more accurate vertical limit setting.
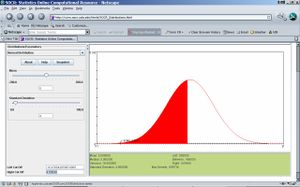
- Questions
- What is the area bound below the Normal density curve on the interval [μ-2σ, μ+2σ]? Does it depend on the values of μ & σ?
- What is the critical value to, that gives P(t>to)=0.025, when t~Tdf=15?
- Which one is larger to or t1, where P(To > to)=P(T1 > t1)=0.025, and To ~ Tdf=15, T1 ~ Tdf=5? What is the limit of to as df--> ∞?
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: