Difference between revisions of "SOCR EduMaterials AnalysisActivities HierarchicalClustering"

From SOCR
Jump to: navigation, search
(Created page with '== SOCR Analysis Hierarchical Clustering Analysis Activity== === Overview === This SOCR Activity demonstrates the utilization of the […')
 
(→‎Hierarchical Clustering Example: Primate Evolution)
 
(18 intermediate revisions by the same user not shown)
Line 2: Line 2:
  
 
=== Overview ===
 
=== Overview ===
−
This SOCR Activity demonstrates the utilization of the [http://socr.ucla.edu/htmls/ana/ SOCR Analyses package] for statistical Computing. In particular, it shows how to use [http://socr.ucla.edu/htmls/ana/ Hierarchical Clustering] and how to interpret the output results.  
+
This SOCR Activity demonstrates the utilization of the [http://socr.ucla.edu/htmls/ana/ SOCR Analyses package] for statistical computing. In particular, it shows how to use [http://socr.ucla.edu/htmls/ana/ Hierarchical Clustering] and how to interpret the output results.
  
−
==Background==  
+
===Background===  
 
[http://en.wikipedia.org/wiki/Hierarchical_clustering Hierarchical Clustering] is a technique of clustering analysis which aims to build a hierarchy (top-down ordering) of clusters. Hierarchical clustering is classified as a connectivity-based clustering algorithm, as it builds models based on distance connectivity (i.e., distances between different clusters). There are various ways to compute the distances – for example, in the single linkage method, the distance between two clusters is computed as the distance between the two closest elements in the two clusters, whereas in the complete linkage method, it is computed as the distance between the two farthest elements in the two clusters. In essence, the paradigm of hierarchical clustering boils down to the following steps:
 
[http://en.wikipedia.org/wiki/Hierarchical_clustering Hierarchical Clustering] is a technique of clustering analysis which aims to build a hierarchy (top-down ordering) of clusters. Hierarchical clustering is classified as a connectivity-based clustering algorithm, as it builds models based on distance connectivity (i.e., distances between different clusters). There are various ways to compute the distances – for example, in the single linkage method, the distance between two clusters is computed as the distance between the two closest elements in the two clusters, whereas in the complete linkage method, it is computed as the distance between the two farthest elements in the two clusters. In essence, the paradigm of hierarchical clustering boils down to the following steps:
 
# Designate every object/item to a new cluster - if you have X items, then there should be X clusters, with each of them containing just one object.  
 
# Designate every object/item to a new cluster - if you have X items, then there should be X clusters, with each of them containing just one object.  
Line 19: Line 19:
  
  
−
===SOCR Hierarchical Clustering Analysis Applet: Data Input===
+
===Hierarchical Clustering Applet: Data Input===
 
Go to [http://socr.ucla.edu/htmls/ana/ SOCR Analyses and select Hierarchical Clustering]  from the drop-down list of SOCR analyses, in the left panel. There are two ways to enter data in the SOCR Hierarchical Clustering applet:
 
Go to [http://socr.ucla.edu/htmls/ana/ SOCR Analyses and select Hierarchical Clustering]  from the drop-down list of SOCR analyses, in the left panel. There are two ways to enter data in the SOCR Hierarchical Clustering applet:
 
* Click on the Example button on the top of the right panel.
 
* Click on the Example button on the top of the right panel.
Line 25: Line 25:
 
* Paste your own data from a spreadsheet into SOCR Hierarchical Clustering data table.  
 
* Paste your own data from a spreadsheet into SOCR Hierarchical Clustering data table.  
  
−
The following is a list of our supported data formats, applying to both ways of inputting (i.e., file “Load” button and copy-paste from spreadsheet)  
+
The following is a list of our supported data formats, applying to both ways of inputting (i.e., file “Load” button and copy-paste from spreadsheet).
−
* Matrix-like file format:
+
* Matrix-like file format: Each line in the text file contains a data matrix row. The characteristics of these files are:  
−
Each line in the text file contains a data matrix row. The characteristics of these files are:  
 
 
** The matrix must be symmetric, and the diagonal elements must be zeros.  
 
** The matrix must be symmetric, and the diagonal elements must be zeros.  
 
** Within each row, the elements are separated by: spaces (‘ ’), tab character,  semicolon (‘;’), comma (‘,’) or vertical bar (‘|’).  
 
** Within each row, the elements are separated by: spaces (‘ ’), tab character,  semicolon (‘;’), comma (‘,’) or vertical bar (‘|’).  
 
** It is possible to include the names in an additional first row or column, but not in both.  
 
** It is possible to include the names in an additional first row or column, but not in both.  
 
** If present, the labels of the nodes can not contain any of the previous separators. Some different representations for the previous matrix could be:
 
** If present, the labels of the nodes can not contain any of the previous separators. Some different representations for the previous matrix could be:
 +
<center>
 +
{| class="wikitable"
 +
|-
 +
! Node_a||Node_b||Node_c||Node_d
 +
|-
 +
| 0.0 || 2.0 || 4.0 || 7.0
 +
|-
 +
| 2.0 || 0.0 || 2.0 || 5.0
 +
|-
 +
| 4.0 || 2.0 || 0.0 || 3.0
 +
|-
 +
| 7.0 || 5.0 || 3.0 || 0.0
 +
|}
 +
</center>
 
   
 
   
−
+
Or it's transpose
−
* List-like file format:
+
 
−
Each line in the text file contains three elements, which represent the labels of two nodes and the distance (or weight) between them. The characteristics of these files are:  
+
<center>
 +
{| class="wikitable"
 +
|-
 +
| Node_a||0.0||2.0||4.0||7.0
 +
|-
 +
| Node_b||2.0||0.0||2.0||5.0
 +
|-
 +
| Node_c||4.0||2.0||0.0||3.0
 +
|-
 +
| Node_d||7.0||5.0||3.0||0.0
 +
|}
 +
</center>
 +
 
 +
* List-like file format: Each line in the text file contains three elements, which represent the labels of two nodes and the distance (or weight) between them. The characteristics of these files are:  
 
** The separators between the three elements may be: spaces (‘ ’), tab character, semicolon (‘;’), comma (‘,’) or vertical bar (‘|’).  
 
** The separators between the three elements may be: spaces (‘ ’), tab character, semicolon (‘;’), comma (‘,’) or vertical bar (‘|’).  
 
** The labels of the nodes can not contain any of the previous separators.  
 
** The labels of the nodes can not contain any of the previous separators.  
Line 41: Line 67:
 
** The Hierarchical Clustering applet accepts either the presence or absence of the symmetric data elements, i.e., if the distance between nodes a and b is 2.0, it is possible to include in the list the line “a b 2.0”, or both “a b 2.0” and “b a 2.0”. If both are present, the program checks if they are equal.  
 
** The Hierarchical Clustering applet accepts either the presence or absence of the symmetric data elements, i.e., if the distance between nodes a and b is 2.0, it is possible to include in the list the line “a b 2.0”, or both “a b 2.0” and “b a 2.0”. If both are present, the program checks if they are equal.  
  
−
====Examples====
+
====Input Data examples====
 
The following simple examples demonstrate the three list‐like files discussed above:
 
The following simple examples demonstrate the three list‐like files discussed above:
 
* Simple list:  
 
* Simple list:  
 +
<center>
 +
{| class="wikitable"
 +
|-
 +
| a||b||2
 +
|-
 +
| a||c||4
 +
|-
 +
| a||d||7
 +
|-
 +
| b||c||2
 +
|-
 +
| b||d||5
 +
|-
 +
| c||d||3
 +
|}
 +
</center>
  
 
* Complete list:  
 
* Complete list:  
−
+
<center>
 +
{| class="wikitable"
 +
|-
 +
| a||b||2
 +
|-
 +
| a||c||4
 +
|-
 +
| a||d||7
 +
|-
 +
| b||a||2
 +
|-
 +
| b||c||2
 +
|-
 +
| b||d||5
 +
|-
 +
| c||a||4
 +
|-
 +
| c||b||2
 +
|-
 +
| c||d||3
 +
|-
 +
| d||a||7
 +
|-
 +
| d||b||5
 +
|-
 +
| d||c||3
 +
|}
 +
</center>
 +
 
 
* Matrix‐like with node labels in the first column, data separated by spaces:
 
* Matrix‐like with node labels in the first column, data separated by spaces:
  
−
<center>[[Image:SOCR_AnalysisActivities_SLR_Chu_072607_Fig1.gif|700px]]</center>
+
<center>
 +
{| class="wikitable"
 +
|-
 +
| 0.0||,||2.0||,||4.0||,||7.0
 +
|-
 +
| || 2.0|| || 0.0  || || 2.0 || 5.0
 +
|-
 +
| 4.0|| || 2.0|| || 0.0|| || 3.0
 +
|-
 +
| 7.0|| &#124; || 5.0||;||3.0|| || 0.0
 +
|}
 +
</center>
 +
 
 +
===Hierarchical Clustering Example: Primate Evolution===
 +
We will demonstrate Hierarchical Clustering using a SOCR built-in example. DNA data representing the molecular phylogeny and evolution of primate mitochondrial DNA is obtained from [[SOCR_EduMaterials_AnalysisActivities_HierarchicalClustering#References|Hayasaka, Gojobori, and Horai (1988)]]. In this homoplasy example, the primate distance matrix was computed by [[SOCR_EduMaterials_AnalysisActivities_HierarchicalClustering#References|Makarenkov and Legendre, (2004)]] and is shown below:
 +
 
 +
* As you start the [http://socr.ucla.edu/htmls/ana/ SOCR Analyses Applet], click on '''Hierarchical Clustering''' from the combo box in the left panel. Here's what the screen should look like.
 +
 
 +
<center>[[Image:SOCR_AnalysisActivities_HierarchicalClustering_Fig1.png|500px]]</center>
 +
 
 +
* The left part of the panel looks like this (make sure that the '''Hierarchical Clustering''' is showing in the drop-down list of analyses, otherwise you won't be able to find the correct dataset and will not be able to reproduce the results!)
 +
 
 +
<center>[[Image:SOCR_AnalysisActivities_HierarchicalClustering_Fig2.png|500px]]</center>
 +
 
 +
* In the SOCR Hierarchical Clustering analysis, there is one SOCR built-in example. Click on the '''Example 1''' button.
 +
 
 +
The dendrogram to the right of the menu bar summarizes the results of Hierarchical Clustering analysis (using unweighted average method) nicely. To change the method used to calculate the distances between clusters, click on the drop-down menu to the right of “Clustering Algorithm” inside the menu bar, and you will see a list of supported methods: Single linkage, complete linage, unweighted average, weighted average, unweighted centroid, weighted centroid and joint between-within. After selecting, click on the “Update” button on the top left, and the dendrogram will then be updated according to the method selected. The user can simultaneous load a text file of correctly formatted data without affecting the current open dendrogram.
 +
 
 +
As you notice, the dendrogram is a preferable way of displaying the algorithm of hierarchical clustering, as it gives the user a birds-eye view of the merging process without losing significant information.
 +
 
 +
<center>
 +
{| class="wikitable"
 +
|-
 +
! Species||Homo_sapiens||Pan||Gorilla||Pongo||Hylobates||Macaca_fuscata||Macaca_mulatta||Macaca_fascicular.||Macaca_sylvanus||Saimiri_sciureus||Tarsius_syrichta||Lemur_catta
 +
|-
 +
|Homo_sapiens||0||0.089||0.104||0.161||0.182||0.232||0.233||0.249||0.256||0.273||0.322||0.308
 +
|-
 +
|Pan||0.089||0||0.106||0.171||0.189||0.243||0.251||0.268||0.249||0.284||0.321||0.309
 +
|-
 +
|Gorilla||0.104||0.106||0||0.166||0.189||0.237||0.235||0.262||0.244||0.271||0.314||0.293
 +
|-
 +
|Pongo||0.161||0.171||0.166||0||0.188||0.244||0.247||0.262||0.241||0.284||0.303||0.293
 +
|-
 +
|Hylobates||0.182||0.189||0.189||0.188||0||0.247||0.239||0.257||0.242||0.269||0.309||0.296
 +
|-
 +
|Macaca_fuscata||0.232||0.243||0.237||0.244||0.247||0||0.036||0.084||0.124||0.289||0.314||0.282
 +
|-
 +
|Macaca_mulatta||0.233||0.251||0.235||0.247||0.239||0.036||0||0.093||0.12||0.293||0.316||0.289
 +
|-
 +
|Macaca_fascicular.||0.249||0.268||0.262||0.262||0.257||0.084||0.093||0||0.123||0.287||0.311||0.298
 +
|-
 +
|Macaca_sylvanus||0.256||0.249||0.244||0.241||0.242||0.124||0.12||0.123||0||0.287||0.319||0.287
 +
|-
 +
|Saimiri_sciureus||0.273||0.284||0.271||0.284||0.269||0.289||0.293||0.287||0.287||0||0.32||0.285
 +
|-
 +
|Tarsius_syrichta||0.322||0.321||0.314||0.303||0.309||0.314||0.316||0.311||0.319||0.32||0||0.252
 +
|-
 +
|Lemur_catta||0.308||0.309||0.293||0.293||0.296||0.282||0.289||0.298||0.287||0.285||0.252||0
 +
|}
 +
</center>
 +
 
 +
Below is the same data where all distance matrix values are converted to integers (multiplying the original values by 1,000).
 +
 
 +
<center>
 +
{| class="wikitable"
 +
|-
 +
! Species||Homo_sapiens||Pan||Gorilla||Pongo||Hylobates||Macaca_fuscata||Macaca_mulatta||Macaca_fascicular.||Macaca_sylvanus||Saimiri_sciureus||Tarsius_syrichta||Lemur_catta
 +
|-
 +
|Homo_sapiens||0||89||104||161||182||232||233||249||256||273||322||308
 +
|-
 +
|Pan||89||0||106||171||189||243||251||268||249||284||321||309
 +
|-
 +
|Gorilla||104||106||0||166||189||237||235||262||244||271||314||293
 +
|-
 +
|Pongo||161||171||166||0||188||244||247||262||241||284||303||293
 +
|-
 +
|Hylobates||182||189||189||188||0||247||239||257||242||269||309||296
 +
|-
 +
|Macaca_fuscata||232||243||237||244||247||0||36||84||124||289||314||282
 +
|-
 +
|Macaca_mulatta||233||251||235||247||239||36||0||93||120||293||316||289
 +
|-
 +
|Macaca_fascicular.||249||268||262||262||257||84||93||0||123||287||311||298
 +
|-
 +
|Macaca_sylvanus||256||249||244||241||242||124||120||123||0||287||319||287
 +
|-
 +
|Saimiri_sciureus||273||284||271||284||269||289||293||287||287||0||320||285
 +
|-
 +
|Tarsius_syrichta||322||321||314||303||309||314||316||311||319||320||0||252
 +
|-
 +
|Lemur_catta||308||309||293||293||296||282||289||298||287||285||252||0
 +
|}
 +
</center>
 +
 
 +
* You can also load these data in the [http://socr.ucla.edu/htmls/SOCR_3DCharts.html SOCR 3D Viewer] (requires Java 3D) (specify 12x12) to see the distance matrix as an image gradient in 3D.
 +
 
 +
<center>[[Image:SOCR_AnalysisActivities_HierarchicalClustering_Fig8.png|500px]]</center>
 +
 
 +
* Load the data into the [http://socr.ucla.edu/htmls/ana/ SOCR Hierarchic Clustering Applet], as shown below:
 +
<center>[[Image:SOCR_AnalysisActivities_HierarchicalClustering_Fig5.png|500px]]</center>
 +
 
 +
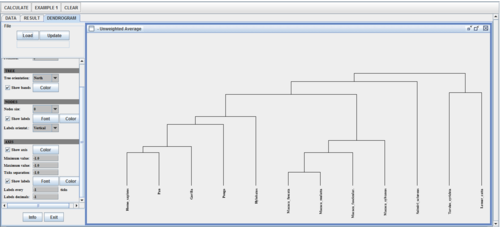
* Run the clustering analysis to get a result like the hierarchical tree shown below:
 +
<center>[[Image:SOCR_AnalysisActivities_HierarchicalClustering_Fig6.png|500px]]</center>
 +
 
 +
* Note that this classification agrees with the phylogenetic tree hierarchy previously reported:
 +
<center>[[Image:SOCR_AnalysisActivities_HierarchicalClustering_Fig7.gif|300px]]</center>
 +
 
 +
===Note===
 +
If you happen to click on the '''Clear''' button in the middle of the procedure, all the data will be cleared out. Simply start over from step 1 and click on an EXAMPLE button for the data you want.
 +
 
 +
===See also===
 +
* [[SOCR_EduMaterials_Activities_2D_PointSegmentation_EM_Mixture|SOCR 2D point classification activity demonstrating Expectation Maximization and mixture modeling]].
  
 +
===References===
 +
* Hayasaka, K., Gojobori, T., Horai, S. (1988) [http://mbe.oxfordjournals.org/content/5/6/626.short Molecular phylogeny and evolution of primate mitochondrial DNA]. Molecular Biology and Evolution 5, 626-644.
 +
* Makarenkov, V, Legendre, P. Desdevises, Y. (2004) [http://onlinelibrary.wiley.com/doi/10.1111/j.1463-6409.2004.00141.x/abstract Modelling phylogenetic relationships using reticulated networks] Zoologica Scripta, 33(1):89–96.
  
 
<hr>
 
<hr>
  
 
{{translate|pageName=http://wiki.stat.ucla.edu/socr/index.php?title=SOCR_EduMaterials_AnalysisActivities_HierarchicalClustering}}
 
{{translate|pageName=http://wiki.stat.ucla.edu/socr/index.php?title=SOCR_EduMaterials_AnalysisActivities_HierarchicalClustering}}

Latest revision as of 15:05, 29 July 2012

SOCR Analysis Hierarchical Clustering Analysis Activity

Overview

This SOCR Activity demonstrates the utilization of the SOCR Analyses package for statistical computing. In particular, it shows how to use Hierarchical Clustering and how to interpret the output results.

Background

Hierarchical Clustering is a technique of clustering analysis which aims to build a hierarchy (top-down ordering) of clusters. Hierarchical clustering is classified as a connectivity-based clustering algorithm, as it builds models based on distance connectivity (i.e., distances between different clusters). There are various ways to compute the distances – for example, in the single linkage method, the distance between two clusters is computed as the distance between the two closest elements in the two clusters, whereas in the complete linkage method, it is computed as the distance between the two farthest elements in the two clusters. In essence, the paradigm of hierarchical clustering boils down to the following steps:

  1. Designate every object/item to a new cluster - if you have X items, then there should be X clusters, with each of them containing just one object.
  2. Calculate the distances between all the current clusters: If each cluster only contains one object, then the distance between each pair is the same as the distance between the objects they contain. If each cluster contain more than one item, then the distance between each pair can be determined using one of the connectivity based methods: Single linkage, complete linage, unweighted average, weighted average, unweighted centroid, weighted centroid, joint between-within, etc.
  3. Based on the distances calculated from step 1, find the closest pair of clusters and merge them into a single cluster, so that there is one less cluster now.
  4. Repeat steps 2 and 3, until all objects are merged into a single cluster of size X.

The results of the above algorithm is usually presented in a dendrogram, which is essentially a tree structure displaying the top-down ordering of clusters under the selected method of distance calculation.

Activity Goals

The goals of this activity are to expose learners to:

  • Inputting data in the correct formats;
  • Reading results of Hierarchical Clustering;
  • Making interpretation of the resulting dendrogram.


Hierarchical Clustering Applet: Data Input

Go to SOCR Analyses and select Hierarchical Clustering from the drop-down list of SOCR analyses, in the left panel. There are two ways to enter data in the SOCR Hierarchical Clustering applet:

  • Click on the Example button on the top of the right panel.
  • Load a text file containing the correctly formatted data by clicking on “Load” button inside the menu bar of DENDROGRAM panel. See below for currently supported data formats.
  • Paste your own data from a spreadsheet into SOCR Hierarchical Clustering data table.

The following is a list of our supported data formats, applying to both ways of inputting (i.e., file “Load” button and copy-paste from spreadsheet).

  • Matrix-like file format: Each line in the text file contains a data matrix row. The characteristics of these files are:
    • The matrix must be symmetric, and the diagonal elements must be zeros.
    • Within each row, the elements are separated by: spaces (‘ ’), tab character, semicolon (‘;’), comma (‘,’) or vertical bar (‘|’).
    • It is possible to include the names in an additional first row or column, but not in both.
    • If present, the labels of the nodes can not contain any of the previous separators. Some different representations for the previous matrix could be:
Node_a Node_b Node_c Node_d
0.0 2.0 4.0 7.0
2.0 0.0 2.0 5.0
4.0 2.0 0.0 3.0
7.0 5.0 3.0 0.0

Or it's transpose

Node_a 0.0 2.0 4.0 7.0
Node_b 2.0 0.0 2.0 5.0
Node_c 4.0 2.0 0.0 3.0
Node_d 7.0 5.0 3.0 0.0
  • List-like file format: Each line in the text file contains three elements, which represent the labels of two nodes and the distance (or weight) between them. The characteristics of these files are:
    • The separators between the three elements may be: spaces (‘ ’), tab character, semicolon (‘;’), comma (‘,’) or vertical bar (‘|’).
    • The labels of the nodes can not contain any of the previous separators.
    • Distances from an element to itself (e.g. “a a 0.0”) must not be included.
    • The Hierarchical Clustering applet accepts either the presence or absence of the symmetric data elements, i.e., if the distance between nodes a and b is 2.0, it is possible to include in the list the line “a b 2.0”, or both “a b 2.0” and “b a 2.0”. If both are present, the program checks if they are equal.

Input Data examples

The following simple examples demonstrate the three list‐like files discussed above:

  • Simple list:
a b 2
a c 4
a d 7
b c 2
b d 5
c d 3
  • Complete list:
a b 2
a c 4
a d 7
b a 2
b c 2
b d 5
c a 4
c b 2
c d 3
d a 7
d b 5
d c 3
  • Matrix‐like with node labels in the first column, data separated by spaces:
0.0 , 2.0 , 4.0 , 7.0
2.0 0.0 2.0 5.0
4.0 2.0 0.0 3.0
7.0 | 5.0 ; 3.0 0.0

Hierarchical Clustering Example: Primate Evolution

We will demonstrate Hierarchical Clustering using a SOCR built-in example. DNA data representing the molecular phylogeny and evolution of primate mitochondrial DNA is obtained from Hayasaka, Gojobori, and Horai (1988). In this homoplasy example, the primate distance matrix was computed by Makarenkov and Legendre, (2004) and is shown below:

  • As you start the SOCR Analyses Applet, click on Hierarchical Clustering from the combo box in the left panel. Here's what the screen should look like.
SOCR AnalysisActivities HierarchicalClustering Fig1.png
  • The left part of the panel looks like this (make sure that the Hierarchical Clustering is showing in the drop-down list of analyses, otherwise you won't be able to find the correct dataset and will not be able to reproduce the results!)
SOCR AnalysisActivities HierarchicalClustering Fig2.png
  • In the SOCR Hierarchical Clustering analysis, there is one SOCR built-in example. Click on the Example 1 button.

The dendrogram to the right of the menu bar summarizes the results of Hierarchical Clustering analysis (using unweighted average method) nicely. To change the method used to calculate the distances between clusters, click on the drop-down menu to the right of “Clustering Algorithm” inside the menu bar, and you will see a list of supported methods: Single linkage, complete linage, unweighted average, weighted average, unweighted centroid, weighted centroid and joint between-within. After selecting, click on the “Update” button on the top left, and the dendrogram will then be updated according to the method selected. The user can simultaneous load a text file of correctly formatted data without affecting the current open dendrogram.

As you notice, the dendrogram is a preferable way of displaying the algorithm of hierarchical clustering, as it gives the user a birds-eye view of the merging process without losing significant information.

Species Homo_sapiens Pan Gorilla Pongo Hylobates Macaca_fuscata Macaca_mulatta Macaca_fascicular. Macaca_sylvanus Saimiri_sciureus Tarsius_syrichta Lemur_catta
Homo_sapiens 0 0.089 0.104 0.161 0.182 0.232 0.233 0.249 0.256 0.273 0.322 0.308
Pan 0.089 0 0.106 0.171 0.189 0.243 0.251 0.268 0.249 0.284 0.321 0.309
Gorilla 0.104 0.106 0 0.166 0.189 0.237 0.235 0.262 0.244 0.271 0.314 0.293
Pongo 0.161 0.171 0.166 0 0.188 0.244 0.247 0.262 0.241 0.284 0.303 0.293
Hylobates 0.182 0.189 0.189 0.188 0 0.247 0.239 0.257 0.242 0.269 0.309 0.296
Macaca_fuscata 0.232 0.243 0.237 0.244 0.247 0 0.036 0.084 0.124 0.289 0.314 0.282
Macaca_mulatta 0.233 0.251 0.235 0.247 0.239 0.036 0 0.093 0.12 0.293 0.316 0.289
Macaca_fascicular. 0.249 0.268 0.262 0.262 0.257 0.084 0.093 0 0.123 0.287 0.311 0.298
Macaca_sylvanus 0.256 0.249 0.244 0.241 0.242 0.124 0.12 0.123 0 0.287 0.319 0.287
Saimiri_sciureus 0.273 0.284 0.271 0.284 0.269 0.289 0.293 0.287 0.287 0 0.32 0.285
Tarsius_syrichta 0.322 0.321 0.314 0.303 0.309 0.314 0.316 0.311 0.319 0.32 0 0.252
Lemur_catta 0.308 0.309 0.293 0.293 0.296 0.282 0.289 0.298 0.287 0.285 0.252 0

Below is the same data where all distance matrix values are converted to integers (multiplying the original values by 1,000).

Species Homo_sapiens Pan Gorilla Pongo Hylobates Macaca_fuscata Macaca_mulatta Macaca_fascicular. Macaca_sylvanus Saimiri_sciureus Tarsius_syrichta Lemur_catta
Homo_sapiens 0 89 104 161 182 232 233 249 256 273 322 308
Pan 89 0 106 171 189 243 251 268 249 284 321 309
Gorilla 104 106 0 166 189 237 235 262 244 271 314 293
Pongo 161 171 166 0 188 244 247 262 241 284 303 293
Hylobates 182 189 189 188 0 247 239 257 242 269 309 296
Macaca_fuscata 232 243 237 244 247 0 36 84 124 289 314 282
Macaca_mulatta 233 251 235 247 239 36 0 93 120 293 316 289
Macaca_fascicular. 249 268 262 262 257 84 93 0 123 287 311 298
Macaca_sylvanus 256 249 244 241 242 124 120 123 0 287 319 287
Saimiri_sciureus 273 284 271 284 269 289 293 287 287 0 320 285
Tarsius_syrichta 322 321 314 303 309 314 316 311 319 320 0 252
Lemur_catta 308 309 293 293 296 282 289 298 287 285 252 0
  • You can also load these data in the SOCR 3D Viewer (requires Java 3D) (specify 12x12) to see the distance matrix as an image gradient in 3D.
SOCR AnalysisActivities HierarchicalClustering Fig8.png
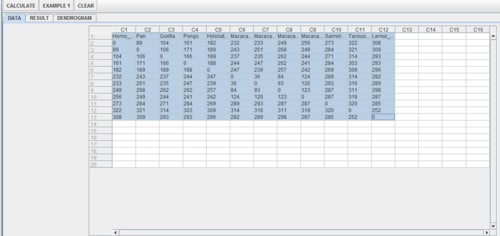
SOCR AnalysisActivities HierarchicalClustering Fig5.png
  • Run the clustering analysis to get a result like the hierarchical tree shown below:
SOCR AnalysisActivities HierarchicalClustering Fig6.png
  • Note that this classification agrees with the phylogenetic tree hierarchy previously reported:
Error creating thumbnail: File missing

Note

If you happen to click on the Clear button in the middle of the procedure, all the data will be cleared out. Simply start over from step 1 and click on an EXAMPLE button for the data you want.

See also

References

Translate this page:

(default)
Uk flag.gif

Deutsch
De flag.gif

Español
Es flag.gif

Français
Fr flag.gif

Italiano
It flag.gif

Português
Pt flag.gif

日本語
Jp flag.gif

България
Bg flag.gif

الامارات العربية المتحدة
Ae flag.gif

Suomi
Fi flag.gif

इस भाषा में
In flag.gif

Norge
No flag.png

한국어
Kr flag.gif

中文
Cn flag.gif

繁体中文
Cn flag.gif

Русский
Ru flag.gif

Nederlands
Nl flag.gif

Ελληνικά
Gr flag.gif

Hrvatska
Hr flag.gif

Česká republika
Cz flag.gif

Danmark
Dk flag.gif

Polska
Pl flag.png

România
Ro flag.png

Sverige
Se flag.gif

Retrieved from "https://wiki.socr.umich.edu/index.php?title=SOCR_EduMaterials_AnalysisActivities_HierarchicalClustering&oldid=11747"