Difference between revisions of "AP Statistics Curriculum 2007 Gamma"
m (→Normal Approximation to Gamma distribution) |
(→Normal Approximation to Gamma distribution) |
||
| Line 65: | Line 65: | ||
Note that if \( \{X_1,X_2,X_3,\cdots \}\) is a sequence of independent [[AP_Statistics_Curriculum_2007_Exponential|Exponential(b) random variables]] then \(Y_k = \sum_{i=1}^k{X_i} \) is a [http://www.math.uah.edu/stat/special/Gamma.html random variable with gamma distribution with some shape parameter], k (positive integer) and scale parameter b. By the [[AP_Statistics_Curriculum_2007_Limits_CLT|central limit theorem]], if k is large, then gamma distribution can be approximated by the normal distribution with mean \(\mu=kb\) and variance \(\sigma^2 =kb^2\). That is, the distribution of the variable \(Z_k={{Y_k-kb}\over{\sqrt{k}b}}\) tends to the standard normal distribution as <math>k\longrightarrow \infty</math>. | Note that if \( \{X_1,X_2,X_3,\cdots \}\) is a sequence of independent [[AP_Statistics_Curriculum_2007_Exponential|Exponential(b) random variables]] then \(Y_k = \sum_{i=1}^k{X_i} \) is a [http://www.math.uah.edu/stat/special/Gamma.html random variable with gamma distribution with some shape parameter], k (positive integer) and scale parameter b. By the [[AP_Statistics_Curriculum_2007_Limits_CLT|central limit theorem]], if k is large, then gamma distribution can be approximated by the normal distribution with mean \(\mu=kb\) and variance \(\sigma^2 =kb^2\). That is, the distribution of the variable \(Z_k={{Y_k-kb}\over{\sqrt{k}b}}\) tends to the standard normal distribution as <math>k\longrightarrow \infty</math>. | ||
| − | For the example above, \(\Gamma(k=4, \theta=2)\), the SOCR Normal Distribution Calculator can be used to obtain an estimate of the area of interest as shown on the image below. | + | For the example above, \(\Gamma(k=4, \theta=2)\), the [http://socr.ucla.edu/htmls/dist/Gamma_Distribution.html SOCR Normal Distribution Calculator] can be used to obtain an estimate of the area of interest as shown on the image below. |
<center>[[Image:EBook_Gamma_Fig2.jpg|500px]]</center> | <center>[[Image:EBook_Gamma_Fig2.jpg|500px]]</center> | ||
| + | The probabilities of the ''real Gamma'' and ''approximate Normal'' distributions (on the range [2:4]) are not identical but are sufficiently close. | ||
| + | |||
| + | <center> | ||
| + | {| class="wikitable" style="text-align:center; width:75%" border="1" | ||
| + | |- | ||
| + | ! Probability||\(\Gamma(k=4, \theta=2)\)||\(Normal(\mu=8, \sigma^2=4)\) | ||
| + | |- | ||
| + | | Mean||8.000000||8.0 | ||
| + | |- | ||
| + | | Median||7.32||8.0 | ||
| + | |- | ||
| + | | Variance||16.0||16.0 | ||
| + | |- | ||
| + | | Standard Deviation||4.0||4.0 | ||
| + | |- | ||
| + | | Max Density|| 0.112021||0.099736 | ||
| + | |- | ||
| + | | <2|| 0.018988|| 0.066807 | ||
| + | |- | ||
| + | | [2:4]|| 0.123888||0.091848 | ||
| + | |- | ||
| + | | >4|| 0.857123||0.841345 | ||
| + | \} | ||
| + | </center> | ||
<hr> | <hr> | ||
Revision as of 12:27, 23 June 2012
Contents
General Advance-Placement (AP) Statistics Curriculum - Gamma Distribution
Gamma Distribution
Definition: Gamma distribution is a distribution that arises naturally in processes for which the waiting times between events are relevant. It can be thought of as a waiting time between Poisson distributed events.
Probability density function: The waiting time until the hth Poisson event with a rate of change \(\lambda\) is
\[P(x)=\frac{\lambda(\lambda x)^{h-1}}{(h-1)!}{e^{-\lambda x}}\]
For \(X\sim \operatorname{Gamma}(k,\theta)\!\), where \(k=h\) and \(\theta=1/\lambda\), the gamma probability density function is given by
\[\frac{x^{k-1}e^{-x/\theta}}{\Gamma(k)\theta^k}\]
where
- e is the natural number (e = 2.71828…)
- k is the number of occurrences of an event
- if k is a positive integer, then \(\Gamma(k)=(k-1)!\) is the gamma function
- \(\theta=1/\lambda\) is the mean number of events per time unit, where \(\lambda\) is the mean time between events. For example, if the mean time between phone calls is 2 hours, then you would use a gamma distribution with \(\theta\)=1/2=0.5. If we want to find the mean number of calls in 5 hours, it would be 5 \(\times\) 1/2=2.5.
- x is a random variable
Cumulative density function: The gamma cumulative distribution function is given by
\[\frac{\gamma(k,x/\theta)}{\Gamma(k)}\]
where
- if k is a positive integer, then \(\Gamma(k)=(k-1)!\) is the gamma function
- \(\textstyle\gamma(k,x/\theta)=\int_0^{x/\theta}t^{k-1}e^{-t}dt\)
Moment generating function: The gamma moment-generating function is
\[M(t)=(1-\theta t)^{-k}\!\]
Expectation: The expected value of a gamma distributed random variable x is
\[E(X)=k\theta\!\]
Variance: The gamma variance is
\[Var(X)=k\theta^2\!\]
Applications
The gamma distribution can be used a range of disciplines including queuing models, climatology, and financial services. Examples of events that may be modeled by gamma distribution include:
- The amount of rainfall accumulated in a reservoir
- The size of loan defaults or aggregate insurance claims
- The flow of items through manufacturing and distribution processes
- The load on web servers
- The many and varied forms of telecom exchange
The gamma distribution is also used to model errors in a multi-level Poisson regression model because the combination of a Poisson distribution and a gamma distribution is a negative binomial distribution.
Example
Suppose you are fishing and you expect to get a fish once every 1/2 hour. Compute the probability that you will have to wait between 2 to 4 hours before you catch 4 fish.
One fish every 1/2 hour means we would expect to get \(\theta=1 / 0.5=2\) fish every hour on average. Using \(\theta=2\) and \(k=4\), we can compute this as follows:
\[P(2\le X\le 4)=\sum_{x=2}^4\frac{x^{4-1}e^{-x/2}}{\Gamma(4)2^4}=0.12388\]
The figure below shows this result using SOCR distributions
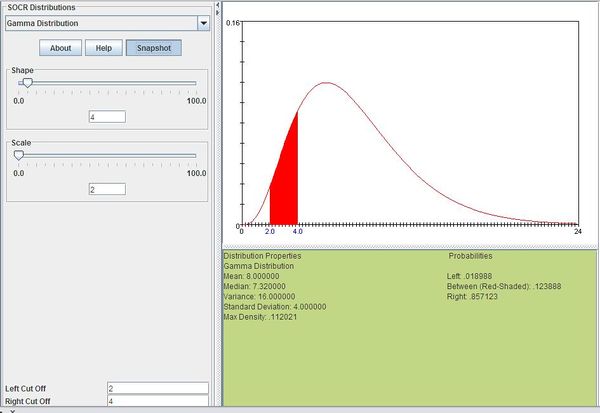
Normal Approximation to Gamma distribution
Note that if \( \{X_1,X_2,X_3,\cdots \}\) is a sequence of independent Exponential(b) random variables then \(Y_k = \sum_{i=1}^k{X_i} \) is a random variable with gamma distribution with some shape parameter, k (positive integer) and scale parameter b. By the central limit theorem, if k is large, then gamma distribution can be approximated by the normal distribution with mean \(\mu=kb\) and variance \(\sigma^2 =kb^2\). That is, the distribution of the variable \(Z_k={{Y_k-kb}\over{\sqrt{k}b}}\) tends to the standard normal distribution as \(k\longrightarrow \infty\).
For the example above, \(\Gamma(k=4, \theta=2)\), the SOCR Normal Distribution Calculator can be used to obtain an estimate of the area of interest as shown on the image below.
The probabilities of the real Gamma and approximate Normal distributions (on the range [2:4]) are not identical but are sufficiently close.
| Probability | \(\Gamma(k=4, \theta=2)\) | \(Normal(\mu=8, \sigma^2=4)\) | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 8.000000 | 8.0 | ||||||||||||||||||||||||
| Median | 7.32 | 8.0 | ||||||||||||||||||||||||
| Variance | 16.0 | 16.0 | ||||||||||||||||||||||||
| Standard Deviation | 4.0 | 4.0 | ||||||||||||||||||||||||
| Max Density | 0.112021 | 0.099736 | ||||||||||||||||||||||||
| <2 | 0.018988 | 0.066807 | ||||||||||||||||||||||||
| [2:4] | 0.123888 | 0.091848 | ||||||||||||||||||||||||
| >4 | 0.857123 | 0.841345
\}
Translate this page: |