Difference between revisions of "SOCR EduMaterials Activities Discrete Distributions"
(→This is an activity to explore the Negaive Binomial Probability Distribution.) |
(→This is an activity to explore the Negative Binomial Probability Distribution.) |
||
| Line 1: | Line 1: | ||
| − | == This is an activity to explore the | + | == This is an activity to explore the Poisson Probability Distribution.== |
* '''Description''': You can access the applets for the above distributions at http://www.socr.ucla.edu/htmls/SOCR_Distributions.html . | * '''Description''': You can access the applets for the above distributions at http://www.socr.ucla.edu/htmls/SOCR_Distributions.html . | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | * '''Exercise 1:''' Use SOCR to graph and print the distribution of a Poisson random variable with <math> \lambda=2 </math>. What is the shape of this distribution? | |
| + | * '''Exercise 2:''' Use SOCR to graph and print the distribution of a Poisson random variable with <math> \lambda=15 </math>. What is the shape of this distribution? What happens when you keep increasing <math> \lambda </math>? | ||
| − | <center>[[Image: | + | * '''Exercise 3:''' Let <math> X \sim Poisson(5) </math>. Find <math> P(3 \le X < 10) </math>, and <math> P(X >10 | X \ge 4) </math>. |
| + | |||
| + | * '''Exercise 4:''' Poisson approximation to binomial: Graph and print <math> X \sim b(60, 0.02) </math>. Approximate this probability distribution using Poisson. Choose three values of <math> X </math> and compute the probability for each one using Poisson and then using binomial. How good is the approximation? | ||
| + | |||
| + | |||
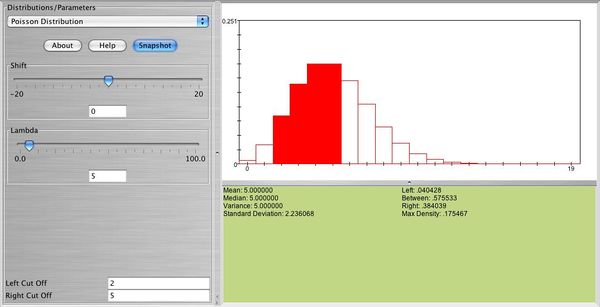
| + | Below you can see the distribution of a Poisson random variable with <math> \lambda=5 </math>. In this graph you can also see the probability that between 2 and 5 events will occur. | ||
| + | |||
| + | |||
| + | <center>[[Image: SOCR_Activities_Christou_poisson.jpg|600px]]</center> | ||
Revision as of 18:23, 27 October 2006
This is an activity to explore the Poisson Probability Distribution.
- Description: You can access the applets for the above distributions at http://www.socr.ucla.edu/htmls/SOCR_Distributions.html .
- Exercise 1: Use SOCR to graph and print the distribution of a Poisson random variable with \( \lambda=2 \). What is the shape of this distribution?
- Exercise 2: Use SOCR to graph and print the distribution of a Poisson random variable with \( \lambda=15 \). What is the shape of this distribution? What happens when you keep increasing \( \lambda \)?
- Exercise 3: Let \( X \sim Poisson(5) \). Find \( P(3 \le X < 10) \), and \( P(X >10 | X \ge 4) \).
- Exercise 4: Poisson approximation to binomial: Graph and print \( X \sim b(60, 0.02) \). Approximate this probability distribution using Poisson. Choose three values of \( X \) and compute the probability for each one using Poisson and then using binomial. How good is the approximation?
Below you can see the distribution of a Poisson random variable with \( \lambda=5 \). In this graph you can also see the probability that between 2 and 5 events will occur.
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
</math>