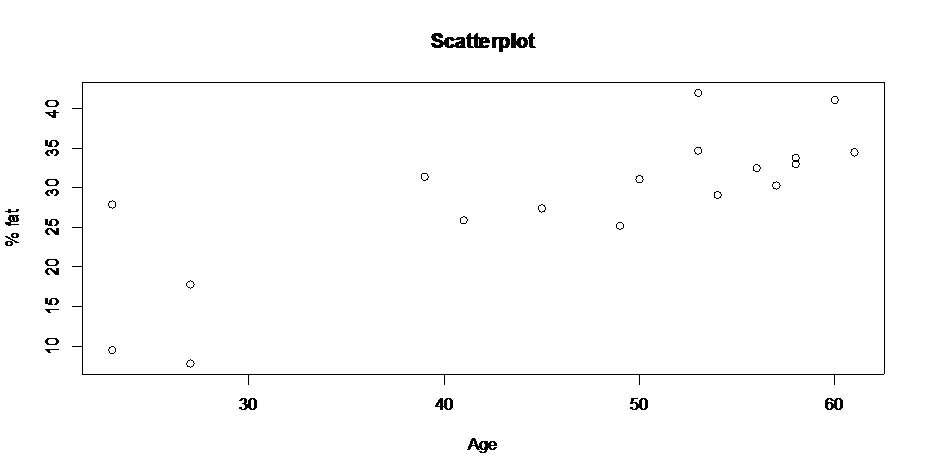SMHS SLR
Contents
Scientific Methods for Health Sciences - Correlation and Simple Linear Regression (SLR)
Overview
Many scientific applications involve the analysis of relationships between two or more variables involved in studying a process of interest. In this section, we are going to study on the correlations between 2 variables and start with simple linear regressions. Consider the simplest of all situations where Bivariate data (X and Y) are measured for a process and we are interested in determining the association with an appropriate model for the given observations. The first part of this lecture will discuss about correlation and then we are going to talk about SLR to address correlations.
Motivation
The analysis of relationships, if any, between two or more variables involved in the process of interest is widely needed in various studies. We begin with the simplest of all situations where bivariate data (X and Y) are measured for a process and we are interested in determining the association, relation or an appropriate model for these observations (e.g., fitting a straight line to the pairs of (X,Y) data). For example, we measured students of their math scores in the final exam and we want to find out if there is any association between the final score and their participation rate in the math class. Or we are interested to find out if there is any association between weight and lung capacity. Simple linear regression would certainly be a simple way to start and it can address the association very well in simple cases.
Theory
- Correlation: correlation efficient (-1≤ρ≤1) is a measure of linear association or clustering around a line of multivariate data. The main relationship between two variables (X,Y) can be summarized by (μ_X,σ_X ),(μ_Y,σ_Y) and the correlation coefficient denoted by ρ=ρ(X,Y).
- The correlation is defined only if both of the standard deviations are finite and are nonzero and it is bounded by -1≤ρ≤1.
- If ρ=1, perfect positive correlation (straight line relationship between the two variables); if ρ=0, no correlation (random cloud scatter), i.e., no linear relation between X and Y; if ρ=-1, a perfect negative correlation between the variables.
- ρ$(X,Y)=\frac{cov(X,Y)}{\sigma_{X}\sigma_{Y}}$=$\frac{E((X-μ_{X})(Y-μ_{Y}))}{\sigma_{X}\sigma_{Y}}$=$\frac{E(XY)-E(X)E(Y)} {\sqrt{E(X^{2})-E^{2}(X)}\sqrt{E(Y^{2})-E^{2}(Y)}},$ where E is the expectation operator, and cov is the covariance. $μ_{X}=E(X),\sigma_{X}^{2}=E(X^{2})-E^{2}(X),$ and similarly for the second variable, Y, and $cov(X,Y)=E(XY)-E(X)*E(Y)$.
- Sample correlation: replace the unknown expectations and standard deviations by sample mean and sample standard deviation: suppose ${X_{1},X_{2},…,X_{n}}$ and ${Y_{1},Y_{2},…,Y_{n}}$ are bivariate observations of the same process and (μ_X,σ_X ),(μ_Y,σ_Y) are the mean and standard deviations for the X and Y measurements respectively. $ρ(x,y)=\frac{\sum x_{i} y_{i}-n\bar{x}\bar{y}}{(n-1)s_{x} s_{y}}$=$\frac{n \sum x_{i} y_{i}-\sum x_{i}\sum y_{i}} {{\sqrt{n\sum x_{i}^{2} -(\sum x_{i})^{2}}} {\sqrt{ n\sum y_{i}^{2}-y_{i})^{2}}}}$
- Example: Human weight and height (suppose we took only 6 of the over 25000 observations of human weight and height included in SOCR dataset .
| Subject Index | Height $(x_{i})$ in cm | Weight $(y_{i})$ in kg | $x_{i}-\bar x$ | $y_{i}-\bar y$ | $(x_{i}-\bar x)^{2}$ | $(y_{i}-\bar y)^{2}$ | $(x_{i}-\bar x)(y_{i}-\bar y)$ |
| 1 | 167 | 60 | 6 | 4.6 | 36 | 21.82 | 28.02 |
| 2 | 170 | 64 | 9 | 8.67 | 81 | 75.17 | 78.03 |
| 3 | 160 | 57 | -1 | 1.67 | 1 | 2.79 | -1.67 |
| 4 | 152 | 46 | -9 | -9.33 | 81 | 87.05 | 83.97 |
| 5 | 157 | 55 | -4 | -0.33 | 16 | 0.11 | 1.32 |
| 6 | 160 | 50 | -1 | -5.33 | 1 | 28.41 | 5.33 |
| Total | 966 | 332 | 0 | 0 | 216 | 215.33 | 195 |
$\bar x\frac {966}{6}=161, \bar y=\frac {322}{6}= 55. s_{x}=\sqrt{\frac{216.5}{5}}=6.57, s_{y}=\sqrt{\frac {215.3}{5}}=6.56.$
$p(x,y)=\frac{1}{n-1}$$\sum\frac{x_{i}-\bar x}{s_{x}}\frac{y_{1}-\bar y}{s_{y}}=0.904$
Slope inference: we can conduct inference based on the linear relationship between two quantitative variables by inference on the slope. The basic idea is that we conduct a linear regression of the dependent variable on the predictor suppose they have a linear relationship and we came up with the linear model of y=α+βx+ε, and β is referred to as the true slope of the linear relationship and α represents the intercept of the true linear relationship on y-axis and ε is the random variation. We have talked about the slope in the linear regression, which describes the change in dependent variable y concerned with change in x.
- Test of the significance of the slope β: (1) is there evidence of a real linear relationship which can be done by checking the fit of the residual plots and the initial scatterplots of y vs. x; (2) observations must be independent and the best evidence would be random sample; (3) the variation about the line must be constant, that is the variance of the residuals should be constant which can be checked by the plots of the residuals; (4) the response variable must have normal distribution centered on the line which can be checked with a histogram or normal probability plot.
- Formula we use:$ t=\frac{b-\beta}{SE_{b}}$ , where b stands for the statistic value, $\beta$ is the parameter we are testing on, $SE_{b}$ is the measure of the variation. For the null hypothesis is the $\beta$=0 that is there is no relationship between y and x, so under the null hypothesis, we have the test statistic $t=\frac {b} {SE_{b}}$.
- Consider a research conducted on see if body fat is associated with age. The data included 18 subjects with the percentage of body fat and the age of the subjects.
| Age | Percentage of Body Fat |
| 23 | 9.5 |
| 23 | 27.9 |
| 27 | 7.8 |
| 27 | 17.8 |
| 39 | 31.4 |
| 41 | 25.9 |
| 45 | 27.4 |
| 49 | 25.2 |
| 50 | 31.1 |
| 53 | 34.7 |
| 53 | 42 |
| 54 | 29.1 |
| 56 | 32.5 |
| 57 | 30.3 |
| 58 | 33 |
| 58 | 33.8 |
| 60 | 41.1 |
| 61 | 34.5 |
The hypothesis tested: $H_{0}:\beta=0$ vs.$H_{a}:\beta\ne0;$ a t-test would be the test we are going to use here given that the data drawn is a random sample from the population.
\#\#\# In R \#\#\#\#\#
\#\# first check the linearity of the relationship using a scatterplot
x <- c(23,23,27,27,39,41,45,49,50,53,53,54,56,57,58,58,60,61) y <- c(9.5,27.9,7.8,17.8,31.4,25.9,27.4,25.2,31.1,34.7,42,29.1,32.5,30.3,33,33.8,41.1,34.5) plot(x,y,main='Scatterplot',xlab='Age',ylab='% fat') cor(x,y) \[1] 0.7920862
The scatterplot shows that there is a linear relationship between x and y, and there is strong positive association of r=0.7920862 which further confirms the eye-bow test from the scatterplot about the linear relationship of age and percentage of body fat. Then we fit a simple linear regression of y on x and draw the scatterplot along with the fitted line:
fit <- lm(y~x)
plot(x,y,main='Scatterplot',xlab='Age',ylab='% fat')
abline(fit)
- SOCR Home page: http://www.socr.umich.edu
Translate this page: