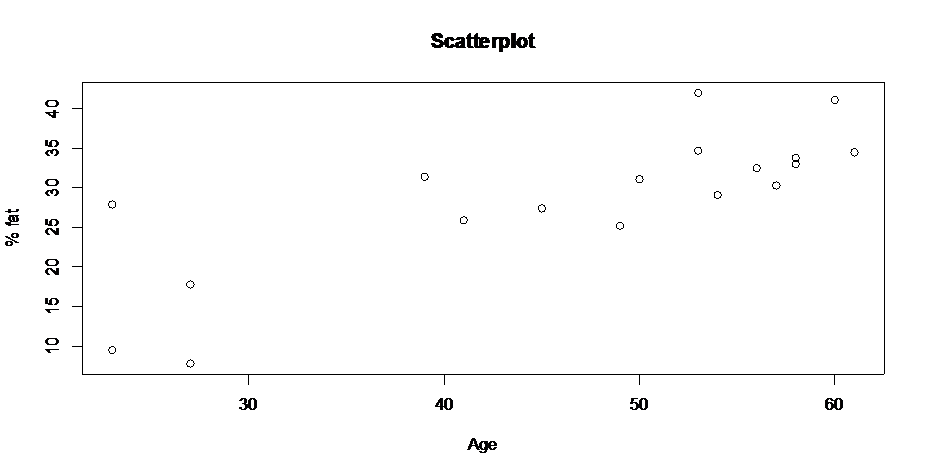SMHS SLR
Contents
Scientific Methods for Health Sciences - Correlation and Simple Linear Regression (SLR)
Overview
Many scientific applications involve the analysis of relationships between two or more variables involved in studying a process of interest. In this section, we are going to study on the correlations between 2 variables and start with simple linear regressions. Consider the simplest of all situations where Bivariate data (X and Y) are measured for a process and we are interested in determining the association with an appropriate model for the given observations. The first part of this lecture will discuss about correlation and then we are going to talk about SLR to address correlations.
Motivation
The analysis of relationships, if any, between two or more variables involved in the process of interest is widely needed in various studies. We begin with the simplest of all situations where bivariate data (X and Y) are measured for a process and we are interested in determining the association, relation or an appropriate model for these observations (e.g., fitting a straight line to the pairs of (X,Y) data). For example, we measured students of their math scores in the final exam and we want to find out if there is any association between the final score and their participation rate in the math class. Or we are interested to find out if there is any association between weight and lung capacity. Simple linear regression would certainly be a simple way to start and it can address the association very well in simple cases.
Theory
- Correlation: correlation efficient (-1≤ρ≤1) is a measure of linear association or clustering around a line of multivariate data. The main relationship between two variables (X,Y) can be summarized by (μ_X,σ_X ),(μ_Y,σ_Y) and the correlation coefficient denoted by ρ=ρ(X,Y).
- The correlation is defined only if both of the standard deviations are finite and are nonzero and it is bounded by -1≤ρ≤1.
- If ρ=1, perfect positive correlation (straight line relationship between the two variables); if ρ=0, no correlation (random cloud scatter), i.e., no linear relation between X and Y; if ρ=-1, a perfect negative correlation between the variables.
- ρ$(X,Y)=\frac{cov(X,Y)}{\sigma_{X}\sigma_{Y}}$=$\frac{E((X-μ_{X})(Y-μ_{Y}))}{\sigma_{X}\sigma_{Y}}$=$\frac{E(XY)-E(X)E(Y)} {\sqrt{E(X^{2})-E^{2}(X)}\sqrt{E(Y^{2})-E^{2}(Y)}},$ where E is the expectation operator, and cov is the covariance. $μ_{X}=E(X),\sigma_{X}^{2}=E(X^{2})-E^{2}(X),$ and similarly for the second variable, Y, and $cov(X,Y)=E(XY)-E(X)*E(Y)$.
- Sample correlation: replace the unknown expectations and standard deviations by sample mean and sample standard deviation: suppose ${X_{1},X_{2},…,X_{n}}$ and ${Y_{1},Y_{2},…,Y_{n}}$ are bivariate observations of the same process and (μ_X,σ_X ),(μ_Y,σ_Y) are the mean and standard deviations for the X and Y measurements respectively. $ρ(x,y)=\frac{\sum x_{i} y_{i}-n\bar{x}\bar{y}}{(n-1)s_{x} s_{y}}$=$\frac{n \sum x_{i} y_{i}-\sum x_{i}\sum y_{i}} {{\sqrt{n\sum x_{i}^{2} -(\sum x_{i})^{2}}} {\sqrt{ n\sum y_{i}^{2}-y_{i})^{2}}}}$
- Example: Human weight and height (suppose we took only 6 of the over 25000 observations of human weight and height included in SOCR dataset .
| Subject Index | Height $(x_{i})$ in cm | Weight $(y_{i})$ in kg | $x_{i}-\bar x$ | $y_{i}-\bar y$ | $(x_{i}-\bar x)^{2}$ | $(y_{i}-\bar y)^{2}$ | $(x_{i}-\bar x)(y_{i}-\bar y)$ |
| 1 | 167 | 60 | 6 | 4.6 | 36 | 21.82 | 28.02 |
| 2 | 170 | 64 | 9 | 8.67 | 81 | 75.17 | 78.03 |
| 3 | 160 | 57 | -1 | 1.67 | 1 | 2.79 | -1.67 |
| 4 | 152 | 46 | -9 | -9.33 | 81 | 87.05 | 83.97 |
| 5 | 157 | 55 | -4 | -0.33 | 16 | 0.11 | 1.32 |
| 6 | 160 | 50 | -1 | -5.33 | 1 | 28.41 | 5.33 |
| Total | 966 | 332 | 0 | 0 | 216 | 215.33 | 195 |
$\bar x\frac {966}{6}=161, \bar y=\frac {322}{6}= 55. s_{x}=\sqrt{\frac{216.5}{5}}=6.57, s_{y}=\sqrt{\frac {215.3}{5}}=6.56.$
$p(x,y)=\frac{1}{n-1}$$\sum\frac{x_{i}-\bar x}{s_{x}}\frac{y_{1}-\bar y}{s_{y}}=0.904$
Slope inference: we can conduct inference based on the linear relationship between two quantitative variables by inference on the slope. The basic idea is that we conduct a linear regression of the dependent variable on the predictor suppose they have a linear relationship and we came up with the linear model of y=α+βx+ε, and β is referred to as the true slope of the linear relationship and α represents the intercept of the true linear relationship on y-axis and ε is the random variation. We have talked about the slope in the linear regression, which describes the change in dependent variable y concerned with change in x.
- Test of the significance of the slope β: (1) is there evidence of a real linear relationship which can be done by checking the fit of the residual plots and the initial scatterplots of y vs. x; (2) observations must be independent and the best evidence would be random sample; (3) the variation about the line must be constant, that is the variance of the residuals should be constant which can be checked by the plots of the residuals; (4) the response variable must have normal distribution centered on the line which can be checked with a histogram or normal probability plot.
- Formula we use:$ t=\frac{b-\beta}{SE_{b}}$ , where b stands for the statistic value, $\beta$ is the parameter we are testing on, $SE_{b}$ is the measure of the variation. For the null hypothesis is the $\beta$=0 that is there is no relationship between y and x, so under the null hypothesis, we have the test statistic $t=\frac {b} {SE_{b}}$.
- Consider a research conducted on see if body fat is associated with age. The data included 18 subjects with the percentage of body fat and the age of the subjects.
| Age | Percentage of Body Fat |
| 23 | 9.5 |
| 23 | 27.9 |
| 27 | 7.8 |
| 27 | 17.8 |
| 39 | 31.4 |
| 41 | 25.9 |
| 45 | 27.4 |
| 49 | 25.2 |
| 50 | 31.1 |
| 53 | 34.7 |
| 53 | 42 |
| 54 | 29.1 |
| 56 | 32.5 |
| 57 | 30.3 |
| 58 | 33 |
| 58 | 33.8 |
| 60 | 41.1 |
| 61 | 34.5 |
The hypothesis tested: $H_{0}:\beta=0$ vs.$H_{a}:\beta\ne0;$ a t-test would be the test we are going to use here given that the data drawn is a random sample from the population.
\#\#\# In R \#\#\#\#\#
\#\# first check the linearity of the relationship using a scatterplot
x <- c(23,23,27,27,39,41,45,49,50,53,53,54,56,57,58,58,60,61) y <- c(9.5,27.9,7.8,17.8,31.4,25.9,27.4,25.2,31.1,34.7,42,29.1,32.5,30.3,33,33.8,41.1,34.5) plot(x,y,main='Scatterplot',xlab='Age',ylab='% fat') cor(x,y) \[1] 0.7920862
The scatterplot shows that there is a linear relationship between x and y, and there is strong positive association of r=0.7920862 which further confirms the eye-bow test from the scatterplot about the linear relationship of age and percentage of body fat. Then we fit a simple linear regression of y on x and draw the scatterplot along with the fitted line:
fit <- lm(y~x)
plot(x,y,main='Scatterplot',xlab='Age',ylab='% fat')
abline(fit)
summary(fit)
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-10.2166 -3.3214 -0.8424 1.9466 12.0753
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.2209 5.0762 0.635 0.535
x 0.5480 0.1056 5.191 8.93e-05 \***
plot(fit$resid,main='Residual Plot')
abline(y=0)
qqnorm(fit$resid) # check the normality of the residuals 300
From the residual plot and the QQ plot of residuals we can see that meet the constant variance and normality requirement with no heavy tails and the regression model is reasonable. From the summary of the regression model we have the t-test on the slope has the t value is 5.191 and the p-value is 8.93 e-05. We can reject the null hypothesis of no linear relationship and conclude that is significant linear relationship between age and percentage of body fat at 5% level of significance.
The confidence interval for the parameter tested is $b±t^{*} SE_{b}$, where b is the slope of the least square regression line, $t^{*}$ is the upper $\frac {1-C} {2}$ critical value from the t distribution with degrees of freedom n-2 and $SE_{b}$ is the standard error of the slope.
The standard error of the slope is 0.1056, so we have the 95% CI of the slope is $(0.5480-0.1056*2.12,0.5480+0.1056*2.12)$, that is (0.324,0.772). So, we are 95% confident that the slope will fall in the range between 0.324 and 0.772.
- Example 2: we are studying on a random sample (size 16) of baseball teams and the data show the team’s batting average and the total number of runs scored for the season.
| Batting average | Number of runs scored |
| 0.294 | 968 |
| 0.278 | 938 |
| 0.278 | 925 |
| 0.27 | 887 |
| 0.274 | 825 |
| 0.271 | 810 |
| 0.263 | 807 |
| 0.257 | 798 |
| 0.267 | 793 |
| 0.265 | 792 |
| 0.254 | 764 |
| 0.246 | 740 |
| 0.266 | 738 |
| 0.262 | 31 |
| .251 | 708 |
In R: x <- c(0.294,0.278,0.278,0.270,0.274,0.271,0.263,0.257,0.267,0.265,0.256,0.254,0.246,0.266,0.262,0.251)
y <- c(968,938,925,887,825,810,807,798,793,792,764,752,740,738,731,708)
cor(x,y)
[1] 0.8654923
The correlation between x and y is 0.8655 which is pretty strong positive correlation. So it would be reasonable to make the assumption of a linear regression model of number of runs scored and the average batting.
fit <- lm(y~x)
summary(fit)
Call:
lm(formula = y ~ x)
Residuals:
- in 1Q Median 3Q Max
-74.427 -26.596 1.899 38.156 57.062
Coefficients:
- Estimate Std. Error t value Pr(>|t|)
(Intercept) -706.2 234.9 -3.006 0.00943 **
x 5709.2 883.1 6.465 1.49e-05 ***
--- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 40.98 on 14 degrees of freedom
Multiple R-squared: 0.7491, Adjusted R-squared: 0.7312
F-statistic: 41.79 on 1 and 14 DF, p-value: 1.486e-05
plot(x,y,main='Scatterplot',xlab='Batting average',ylab='Number of runs')
abline(fit)
par(mfrow=c(1,2))
plot(fit$resid,main='Residual Plot')
abline(y=0)
qqnorm(fit$resid)
The estimated value of the slope is 5709.2, standard error 833.1, t value = 6.465, and the p-value is 1.49 e-05, so we reject the null hypothesis and conclude that there is significant linear relationship between the average batting and the number of runs. We have the 95% CI of the slope is $(5709.2-833.1*2.145,5709.2+833.1*2.145)$, that is $(3922.2,7496.2)$. So, we are 95% confident that the slope will fall in the range between 3922.2 and 7496.2.
You can also use SOCR SLR Analysis Simple Regression to copy-paste the data in the applet, estimate regression slope and intercept and compute the corresponding statistics and p-values.
Simple Linear Regression Results: Mean of C1 = 46.33333 Mean of C2 = 28.61111 Regression Line: C2 = 3.22086 + 0.5479910213243551 C1 Correlation(C1, C2) = .79209 R-Square = .62740 Intercept: Parameter Estimate: 3.22086 Standard Error: 5.07616 T-Statistics: .63451 P-Value: .53472 Slope: Parameter Estimate: .54799 Standard Error: .10558 T-Statistics: 5.19053 P-Value: .00009
- SOCR Home page: http://www.socr.umich.edu
Translate this page: