SMHS NonParamInference

Scientific Methods for Health Sciences - Non-Parametric Inference

Overview

Nonparametric inference is descriptive and inferential statistics made that are not based on parametrized families of probability distributions, which is the basis of the parametric inference we discussed in HS 550. That is, nonparametric inference made no assumptions about the probability distributions of the variables assessed and the model structure is not specified a priori but is determined from data instead. The term nonparametric is not strictly referring to models completely lack of parameters but that the number and nature of the parameters are flexible and not fixed in advance. In this lecture, we are going to introduce to the area of nonparametric inference and illustrate various nonparametric inference applications with examples.

Motivation

We have discussed about parametric inference where the inference is made based on the assumptions of the probability distributions of the variables being assessed. What if such an assumption is violated and variables studied cannot be categorized into a parametrized family of probability distribution? Distribution-free (nonparametric) statistical methods would be the answer to solving problems in such situation.

Theory

Differences of Median of Two Paired Samples: the sign test and the Wilcoxon signed rand test are the simplest nonparametric tests, which are also alternatives to the one-sample and paired t-test.

• Motivational Clinical Example: the relative risk of mortality from 16 studies of septic patients is reported, which measures whether the patients developed complications of acute renal failure. A relative risk of 1.0 means no effect and relative risk ≠1 suggests beneficial or detrimental effect of developing acute renal failure in sepsis. The main goal was to determine whether developing acute renal failure as a complication of sepsis impacts patient mortality from the cumulative evidence in these 16 studies and the data is recorded as below. The data is heavily skewed and not bell-shaped and apparently not normally distributed, so the traditional paired t-test fails here.

Study	Relative Risk	Sign (Relative Risk -1)
1	0.75	-
2	2.03	+
3	2.29	+
4	2.11	+
5	0.80	-
6	1.50	+
7	0.79	-
8	1.01	+
9	1.23	+
10	1.48	+
11	2.45	+
12	1.02	+
13	1.03	+
14	1.30	+
15	1.54	+
16	1.27	+

• The Sign Test: a nonparametric alternative to the One-Sample and Paired T-Test and doesn’t require the data to be normally distributed. It assigns a positive (+) or negative (-) sign to each observation according to whether it is greater or less than some hypothesized value. It measures the difference between the ± signs and how distinct the difference is from our expectations to observe by chance alone. For the motivational example, if there were no effects of developing acute renal failure on the outcome from sepsis, about half of the 16 studies above would be expected to have a relative risk less than 1.0 (a "-" sign) and the remaining 8 would be expected to have a relative risk greater than 1.0 (a "+" sign). In the actual data, 3 studies had "-" signs and the remaining 13 studies had "+" signs. Intuitively, this difference of 10 appears large to be simply due to random variation. If so, the effect of developing acute renal failure would be significant on the outcome from sepsis.
  • Calculations: suppose $N_{+}$ is the number of “+” signs and the significance level $\alpha=0.05$; the hypotheses: $H_{0}:N_{+}=8$;vs.$H_{a}$: $N_{+}≠8$ (the effect of developing acute renal failure is not significant on the outcome from sepsis vs. the effect of developing acute renal failure is significant on the outcome from sepsis). Define the following test statistics: $B_{S}=max(N_{+},N_{-})$, where $N_{+}$ and $N_{-}$ are the number of positive and negative sings respectively. For the example above, we have $B_{S}=max(N_{+},N_{-})=max(13,3)=13$ and the probability that such binomial variable exceeds 13 is P$(Bin(16,0.5,13))=0.010635$. Therefore, we can reject the null hypothesis $H_{0}$ and conclude that the significant effect of developing acute renal failure on the outcome from sepsis.
  • Example of set of 12 identical twins given psychological tests to determine whether the first born of the set tends to be more aggressive than the second born. Each twin is scored according to aggressiveness; a higher score indicates greater aggressiveness. Because of nature pairing in a set of twins these data can be considered paired.

Twin-Index	1st Born	2nd Born	Sign
1	86	88	-
2	71	77	-
3	77	76	+
4	68	64	+
5	91	96	-
6	72	72	0 (Drop)
7	77	65	+
8	91	90	+
9	70	65	+
10	71	80	-
11	88	81	+
12	87	72	+

First plot the data using SOCR Linear Chart SOCR Linear Chart and observe that there seems to be no strong effect of the order of birth on baby’s regression.

Next, use the SOCR Sign Test Analysis to quantitatively evaluate the evidence to reject the null hypothesis that there is no birth-order effect on baby’s aggressiveness. (p-value of 0.274 => don’t reject the null hypothesis at 5% level of significance.)

• The Wilcoxon Signed Rank Test: comparisons of differences between measurements and requires that the data are measured at an interval level of measurements but does not require assumptions about the form of the distribution of the measurements. It is used whenever the distributional assumption of the t-test is not satisfied.
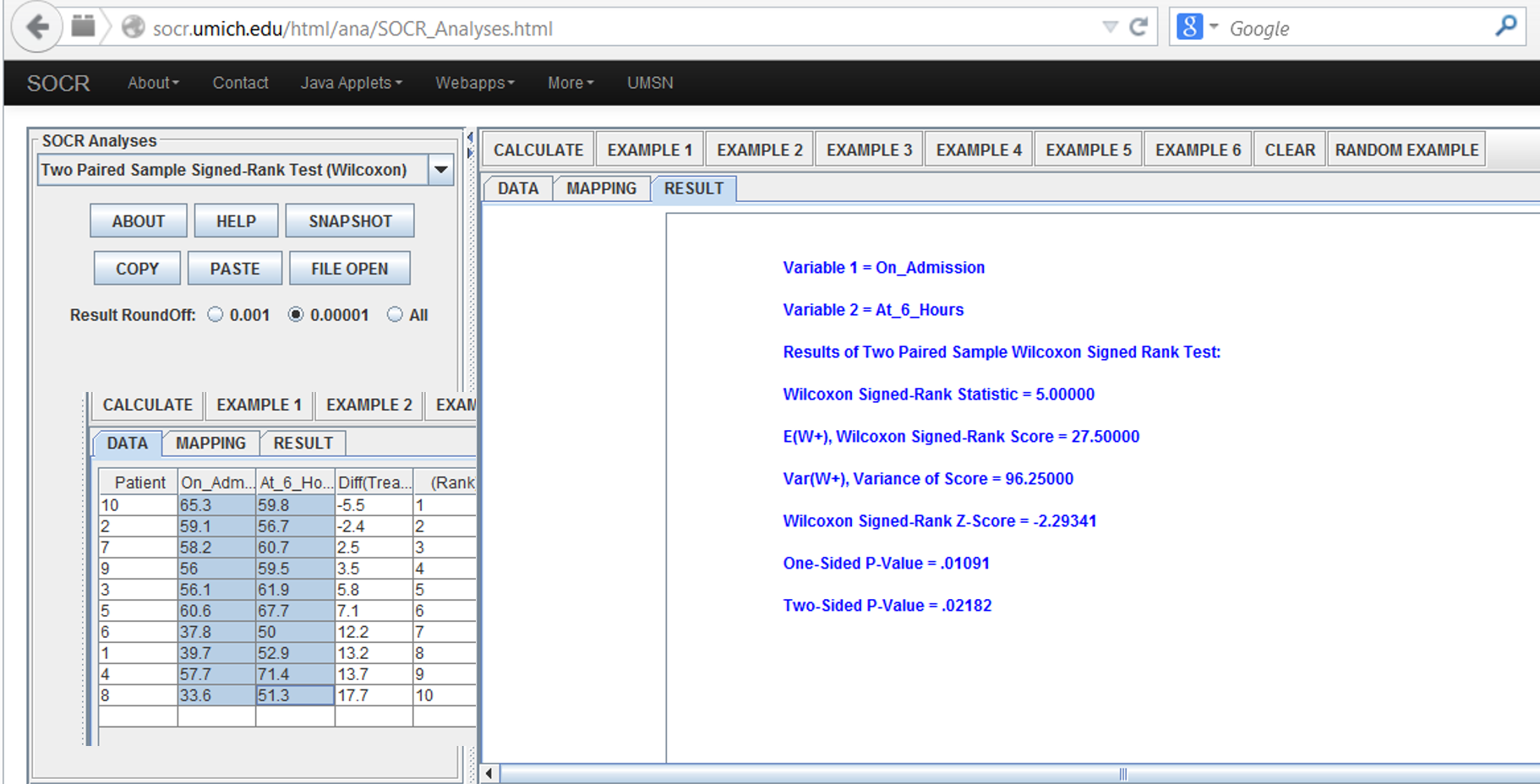
  • Motivational example: data on the central venous oxygen saturation $(SvO_{2}$(%)) from 10 consecutive patients at 2 time points, at admission and 6 hours after admission to the intensive care unit (ICU) are recorded. $H_{0}$: there is no effect of 6 hours of ICU treatment on $SvO_{2}$, which states that the mean of the differences between $SvO_{2}$ at admission and that 6 hours after admission should be zero. The data are recorded as below:

Patient	On Admission	At 6 Hours	Difference	Rank
2	59.1	56.7	-2.4	1
7	58.2	60.7	2.5	2
9	56.0	59.5	3.5	3
10	65.3	59.8	-5.5	4
3	56.1	61.9	5.8	5
5	60.6	67.7	7.1	6
6	37.8	50.0	12.2	7
1	39.7	52.9	13.2	8
4	57.7	71.4	13.7	9
8	33.6	51.3	17.7	10

Result: the one-sided and two-sided alternative hypotheses p-values for the Wilcoxon Signed Rank Test reported by the SOCR Analysis are 0.011 and 0.022 respectively. Result output and interpretation:

Variable 1 = At_Admission

Variable 2 = 6_Hrs_Later

Results of Two Paired Sample Wilcoxon Signed Rank Test:

Wilcoxon Signed-Rank Statistic = 5.000: [data-driven estimate of the Wilcoxon Signed-Rank Statistic]. E(W+), Wilcoxon Signed-Rank Score = 27.500: [Wilcoxon Signed-Rank Score = expectation of the Wilcoxon Signed-Rank Statistic].

Var(W+), Variance of Score = 96.250: [Variance of Score = variance of the Wilcoxon Signed-Rank Statistic]. Wilcoxon Signed-Rank Z-Score = -2.293 $[Z-score=\frac{W_{stat}-E(W_{+})}{\sqrt{Var(W_{+})}}]$.

One-Sided P-Value = .011: [the one-sided (uni-directional) probability value expressing the strength of the evidence in the data to reject the null hypothesis that the two populations have the same medians (based on Gaussian, standard Normal, distribution)].

Two-Sided P-Value = .022: [the double-sided (non-directional) probability value expressing the strength of the evidence in the data to reject the null hypothesis that the two populations have the same medians (based on Gaussian, standard Normal, distribution)].

3.2) Difference of Medians of Two Independent Samples: the Wilcoxon-Mann-Whitney (WMW) test is nonparametric test of assessing whether two samples from the same distribution.

• Motivational Example: 9 observations of surface soil PH were made at two different independent locations. There is no pairing in this design though this is a balanced design with 9 observations in each group. The question is does the data suggest that the true mean soil PH values differs for the two locations. Testing using α=0.05 and be sure to check any necessary assumptions for the validity of the test.

Location 1	Location 2
8.10	7.85
7.89	7.30
8.00	7.73
7.85	7.27
8.01	7.58
7.82	7.27
7.99	7.50
7.80	7.23
7.93	7.41

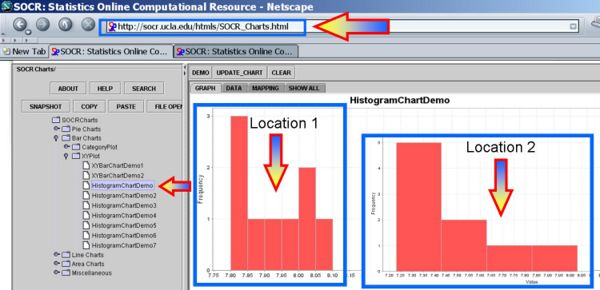
Plot the data and we can see that the distributions may be different or not even symmetric, unimodal and bell-shaped. Therefore, the independent t-test fails to test a Null-hypothesis that the centers of the two distributions are identical.

The first figure shows the index plot of the pH levels for both samples. The second figure shows the sample histograms of these samples, which are clearly not Normal-like. Therefore, the independent t-test would not be appropriate to analyze these data.

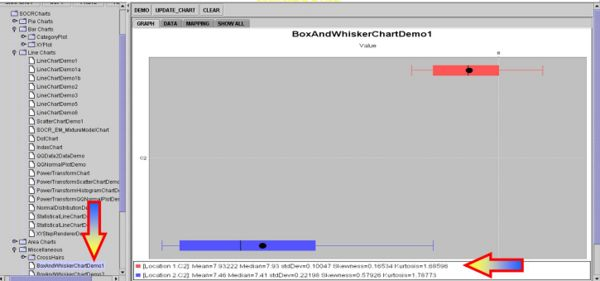
Intuitively, we may consider these group differences significantly large, especially if we look at the Box-and-Whisker Plots, but this is a qualitative inference that demands a more quantitative statistical analysis that can back up our intuition.

• The Wilcoxon-Mann-Whitney Test (WMW): a non-parametric test for assessing whether two samples come from the same distribution. The null hypothesis is that the two samples are drawn from a single population, and therefore that their probability distributions are equal. It requires that the two samples are independent, and that the observations are ordinal or continuous measurements.
• Calculations: The U statistic for the WMW test may be approximated for sample sizes above about 20 using the normal distribution. The U test is provided as part of SOCR analyses http://socr.umich.edu/html/ana/
  • For small samples: (1) Choose the sample for which the ranks seem to be smaller. Call this Sample 1, and call the other sample Sample 2; (2) Taking each observation in Sample 2, count the number of observations in Sample 1 that are smaller than it (count 0.5 for any that are equal to it); (3) The total of these counts is U.
  • For larger samples: (1) Arrange all the observations into a single ranked series. That is, rank all the observations without regard to which sample they come from; (2) Add up the ranks in Sample 1, The sum of ranks in Sample 2 follows by calculation, since the sum of all the ranks equals N (N + 1)/2, where N is the total number of observations; (3) U is given by the formula: U_1=R_1-(n_1 (n_1+1))/2, where n_1 is the two sample size for Sample 1, and R_1 is the sum of the ranks in Sample 1. there is no specification as to which sample is considered Sample 1. An equally valid formula for U is U_2=R_2-(n_2 (n_2+1))/2, the sum of the two values is given by U_1+U_2=R_1-(n_1 (n_1+1))/2+R_2-(n_2 (n_2+1))/2. Given that R_1+R_2=N(N+1)/2 and N=n_1+n_2, hence we have U_1+U_2=n_1 n_2. The maximum value of U is the product of the sample sizes.
• Application using SOCR analyses: it is much quicker to use SOCR analyses to compute the statistical significance of the sign test.

Clearly the p value < 0.05 and therefore our data provides sufficient evidence to reject the null hypothesis. So we assume that there were significant PH differences between the two soil lots tested in this experiment.

One-sided P-value for Sample 2 < Sample 1 = 0.00040.

Two-sided P-value for Sample 1 not equal to Sample 2 = 0.00079.

• The WMW Tess vs. Independent T-test: Both types of tests answer the same question but they treat data differently.
  • The WMW test uses rank ordering: Positive: Doesn’t depend on normality or population parameters Negative: Distribution free lacks power because it doesn't use all the info in the data
  • The T-test uses the raw measurements: Positive: Incorporates all of the data into calculations Negative: Must meet normality assumption
  • Neither test is uniformly superior. If the data are normally distributed we use the T-test. If the data are not normal use the WMW test.

3.3) Differences of Proportions of Two Samples: depending upon whether the samples are dependent or independent where different statistical tests are applied.

• Differences of proportions of two independent samples: If the samples are independent and we are interested in the differences in the proportions of subjects of the same trait (a characteristic of each observation, e.g., gender) we need to use the standard proportion tests. For small sample sizes, we use corrected proportion (p ̃) that and we use the raw sample proportion (p ̂) in large samples.
• Differences of proportions of two paired samples: If the samples are paired, then we can employ the McNemar's non-parametric test for differences in proportions in matched pair samples. It is most often used when the observed variable is a dichotomous variable (presence or absence of a trait/characteristic for each observation).
• Example: suppose a medical doctor is interested in determining the effect of a drug on a particular disease (D). Suppose the doctor conducts a study and records the frequencies of incidence of the disease (D+ and D− ) in a random population before the treatment with the new drug takes place. Then the doctor prescribes the treatment to all subjects and records the incidence of the disease in the rows following the treatment. The test requires the same subjects to be included in the before- and after-treatment measurements (matched pairs).

		Before Treatment
		D +	D −	Total
After Treatment	D +	a=101	b=59	a+b=160
	D −	c=121	d=33	c+d=154
	Total	a+c=222	b+d=92	a+b+c+d=314

• • Marginal homogeneity occurs when the row totals equal to the column totals, a and d in each equation can be cancelled; leaving b equal to c: a+b=a+c, c+d=b+d. In this example, marginal homogeneity would mean there was no effect of the treatment.
  • The mcNemar statistic is shown: χ_0^2=(b-c)^2/(b+c)~χ_(df=1)^2
  • The marginal frequencies are not homogeneous if the χ_0^2 result is significant p < 0.05. If b and/or c are small (b + c < 20) then χ_0^2 is not approximated by the Chi-Square Distribution and a Sign Test should instead be used.
  • An interesting observation when interpreting McNemar's test is that the elements of the main diagonal contribute no information whatsoever to the decision if (in the above example) pre- or post-treatment condition is more favorable.
• General McNemar test of marginal homogeneity for a single category: If we have observed measurements on a K-level categorical variable -- e.g., agreement between two evaluators summarized by a K×K classification table, where each row or column contains the number of individuals rated as part of this group by each evaluator. For instance, two instructors may evaluate students as 1=poor, 2=good and 3=excellent. There could be significant differences in the evaluations of the same students by the 2 instructors. Suppose we are interested in whether the proportions of students rated excellent by the 2 instructors are the same. Then we'll pool the poor and good categories together and form a 2x2 table that we can then use the 2x2 McNemar test statistics on, as shown below.

		Evaluator 2
		Poor	Good	Excellent	Total
Evaluator 1	Poor	5	15	4	24
	Good	16	10	9	35
	Excellent	11	17	13	41
	Total	32	42	26	100

		Evaluator 2
		Poor	Good or Excellent	Total
Evaluator 1	Poor	a=5	b=19	a+b=24
	Good or Excellent	c=27	d=49	c+d=76
	Total	a+c=32	b+d=68	a+b+c+d=100

To test marginal homogeneity for one single category (in this case poor evaluation) means to test row/column marginal homogeneity for the first category (poor). This is achieved by collapsing all rows and columns corresponding to the other categories.

χ_o^2=(b-c)^2/(b+c)=(-8)^2/46=1.39 ~ χ_(df=1)^2 P( χ_(df=1)^2>1.39)=0.238405

Therefore, we don’t have sufficient evidence to reject the null hypothesis of two evaluators were consistent in their ratings of students.

3.4) Differences of Means of Several Independent Samples: extend the multi-sample inference discussed in ANOVA to the situation where ANOVA assumptions are invalid.

• Motivational Example: Suppose four groups of students are randomly assigned to be taught with four different techniques, and their achievement test scores are recorded. Are the distributions of test scores the same, or do they differ in location? The data is presented in the table below. The small sample sizes and the lack of distribution information of each sample illustrate how ANOVA may not be appropriate for analyzing these types of data.

Teaching Method
	Method 1	Method 2	Method 3	Method 4
Index	65	75	59	94
	87	69	78	89
	73	83	67	80
	79	81	62	88

• The Kruskal-Wallis Test: Kruskal-Wallis One-Way Analysis of Variance by ranks is a non-parametric method for testing equality of two or more population medians. Intuitively, it is identical to a One-way Analysis of Variance with the raw data (observed measurements) replaced by their ranks. Since it is a non-parametric method, the Kruskal-Wallis Test does not assume a normal population, unlike the analogous one-way ANOVA. However, the test does assume identically-shaped distributions for all groups, except for any difference in their centers (e.g., medians).
  • Calculations: Let N be the total number of observations and N=∑_(i=1)^k▒n_i and R(X_ij) be the rank assigned to X_ij and let R_i be the sum of ranks assigned to the i^th sample and R_i=∑_(i=1)^(n_i)▒〖R(X_ij)〗,i=1,2,…,k.

The SOCR program computes R_i for each sample. The test statistic is defined for the following formulation of hypotheses:

H_o: All of the k population distribution functions are identical.

H_a: At least one of the populations tends to yield larger observations than at least one of the other populations.

Suppose {X_(i,1),X_(i,2),…,X_(i,n_i ) } represents the values of the i^th sample, where i≤i≤k. Test statistics: T=(1/S^2)∑_(i=1)^k▒R_i^2 /n_i-N(N+1)^2/4, where S^2=(1/(N-1) ∑▒〖R(X_ij )^2 〗-N(N+1))^2/4.

Note: If there are no ties, then the test statistic is reduced to:

T=12/N(N+1) ∑_(i=1)^k▒(R_i^2)/n_i -3(N+1).

However, the SOCR implementation allows for the possibility of having ties; so it uses the non-simplified, exact method of computation. Multiple comparisons have to be done here. For each pair of groups, the following is computed and printed at the Result Panel.

|R_i/n_i -R_j/n_j |>t_(1-α/2) ((S^2 (N-1-T))/(N-K))^(1/2)/(1/n_i +1/n_j )^(1/2)

The SOCR computation employs the exact method instead of the approximate one (Conover 1980), since computation is easy and fast to implement and the exact method is somewhat more accurate.

• The Kruskal-Wallis Test Using SOCR Analyses: It is much quicker to use SOCR Analyses to compute the statistical significance of this test. This SOCR Kruskal-Wallis Test Activity may also be helpful in understanding how to use this test in SOCR. For the teaching-methods example above, we can easily compute the statistical significance of the differences between the group medians (centers):

Clearly, there is only one significant group difference between medians, after the multiple testing correction, for the group1 vs. group4 comparison (see below):

Group Method1 vs. Group Method2: 1.0 < 5.2056

Group Method1 vs. Group Method3: 4.0 < 5.2056

Group Method1 vs. Group Method4: 6.0 > 5.2056

Group Method2 vs. Group Method3: 5.0 < 5.2056

Group Method2 vs. Group Method4: 5.0 < 5.2056

Group Method3 vs. Group Method4: 10.0 > 5.2056

3.5) Differences of Variances of Independent Samples (variance homogeneity): different tests for variance equality can be applied. It is frequently necessary to test if k samples have equal variances. Homogeneity of variances is often a reference to equal variances across samples. Some statistical tests, for example the analysis of variance, assume that variances are equal across groups or samples.

• Calculation: The (modified) Fligner-Killeen test (the median-centering Fligner-Killeen test) provides the means for studying the homogeneity of variances of k populations { X_ij, for 1≤i≤n_j and 1≤j≤k}. The test jointly ranks the absolute values of |X_ij-(X_j ) ̃| and assigns increasing scores a_Ni=Φ^(-1) ((1+i/(N+1)))/2, based on the ranks of all observations. In this test, (X_j ) ̃ is the sample median of the j^th population, and Φ(.) is the cumulative distribution function for Normal distribution.
  • Fligner-Killeen test statistics: χ_o^2=(∑_(j=1)^k▒〖n_j ((A_j ) ̅-a ̅ )^2 〗)/V^2 , where (A_j ) ̅ is the mean score for the j^th sample, a ̅ is the overall mean score of all a_Nj and V^2 is the sample variance of all scores. We have N=∑_(j=1)^k▒n_j ,(A_j ) ̅=1/n_j ∑_(j=1)^(n_j)▒a_(Nm_i ) , where a_(Nm_i ) is the increasing rank score for the i^th observation in the j^th sample, a ̅=1/N ∑_(i=1)^N▒a_Ni ,V^2=1/(N-1) ∑_(i=1)^N▒(a_Ni-a ̅ )^2 .
  • Fligner-Killeen probabilities: for large sample size, the modified Fligner-Killeen test statistic has an asymptotic chi-square distribution with k-1 degrees of freedom χ_o^2~χ_(k-1)^2.

Applications

4.1) This article (http://www.jstor.org/discover/10.2307/2958850?uid=3739728&uid=2&uid=4&uid=3739256&sid=21103957523251) presents a general introduction to nonparametric inference and the model involved and studied the existence of complete and sufficient statistics for this model. It gives an empirical process estimating the model and generalized the empirical cumulative hazard rate from survival analysis. Consistency and weak convergence results were given and tests for comparison of two counting processes, generalizing the two sample rank tests are defined and studied. Finally, it gives an application to a set of biological data.

4.2) This article (http://projecteuclid.org/euclid.aos/1033066215) presents a study relates a different solution to the challenge of constructing a sequence of functions, each based on only finite segments of the past, which together provide a strongly consistent estimator for the conditional probability of the next observation, given the infinite past. It also studied on some extensions to regression, pattern recognition and on-line forecasting.

Software

http://wiki.stat.ucla.edu/socr/index.php/SOCR_EduMaterials_AnalysisActivities_TwoPairedSign

http://www.socr.ucla.edu/htmls/ana/TwoPairedSampleSign-Test_Analysis.html

Problems

6.1) Suppose 10 randomly selected rats were chosen to see if they could be trained to escape a maze. The rats were released and timed (seconds) before and after 2 weeks of training (N means the rat did not complete the maze-test). Do the data provide evidence to suggest that the escape time of rats is different after 2 weeks of training? Test using α = 0.05.

Rat	Before	After	Sign
1	100	50	+
2	38	12	+
3	N	45	+
4	122	62	+
5	95	90	+
6	116	100	+
7	56	75	-
8	135	52	+
9	104	44	+
10	N	50	+

6.2) Automated brain volume segmentation is an important step in many modern computational brain mapping studies. Suppose we have two separate and competing versions of automated brain parsing (segmentation) algorithms that automatically tessellate (partition) the brain into 57 separate regions of interest (ROI’s). An important question then is how consistent are these 2 different techniques, across the 57 ROIs. We can use the ROI volume as a measure of the resulting automated brain parcellation and compare the paired differences between the 2 methods across all ROIs. The image shows an example of a brain parcellated into these 57 regions and the table below contains the volumes of the 57 ROIs for the 2 different brain tessellation techniques. Use appropriate SOCR analyses and relevant SOCR charts to argue whether or not the 2 different methods are consistent and agree on their ROI labels.

Index	Volume_Intensity	ROI_Name	Method1_Volume	Method2_Volume
1	0	Background	9236455	9241667
2	21	L_superior_frontal_gyrus	78874	78693
3	22	R_superior_frontal_gyrus	69575	74391
4	23	L_middle_frontal_gyrus	67336	68872
5	24	R_middle_frontal_gyrus	68344	67024
6	25	L_inferior_frontal_gyrus	31912	21479
7	26	R_inferior_frontal_gyrus	26264	29035
8	27	L_precentral_gyrus	28942	33584
9	28	R_precentral_gyrus	35192	30537
10	29	L_middle_orbitofrontal_gyrus	10141	11608
11	30	R_middle_orbitofrontal_gyrus	9142	11850
12	31	L_lateral_orbitofrontal_gyrus	7164	5382
13	32	R_lateral_orbitofrontal_gyrus	5964	4947
14	33	L_gyrus_rectus	3840	1995
15	34	R_gyrus_rectus	2672	2994
16	41	L_postcentral_gyrus	24586	27672
17	42	R_postcentral_gyrus	21736	28159
18	43	L_superior_parietal_gyrus	25791	27500
19	44	R_superior_parietal_gyrus	28850	32674
20	45	L_supramarginal_gyrus	16445	22373
21	46	R_supramarginal_gyrus	11893	11018
22	47	L_angular_gyrus	20740	22245
23	48	R_angular_gyrus	20247	17793
24	49	L_precuneus	14491	12983
25	50	R_precuneus	15589	16323
26	61	L_superior_occipital_gyrus	6842	6106
27	62	R_superior_occipital_gyrus	5673	6539
28	63	L_middle_occipital_gyrus	15011	19085
29	64	R_middle_occipital_gyrus	19063	25747
30	65	L_inferior_occipital_gyrus	10411	8675
31	66	R_inferior_occipital_gyrus	12142	12277
32	67	L_cuneus	6935	9700
33	68	R_cuneus	7491	11765
34	81	L_superior_temporal_gyrus	29962	34934
35	82	R_superior_temporal_gyrus	30630	28788
36	83	L_middle_temporal_gyrus	27558	19633
37	84	R_middle_temporal_gyrus	26314	25301
38	85	L_inferior_temporal_gyrus	24817	24885
39	86	R_inferior_temporal_gyrus	25088	20661
40	87	L_parahippocampal_gyrus	6761	6977
41	88	R_parahippocampal_gyrus	6529	7964
42	89	L_lingual_gyrus	16752	14748
43	90	R_lingual_gyrus	20914	18500
44	91	L_fusiform_gyrus	16565	15020
45	92	R_fusiform_gyrus	14409	17311
46	101	L_insular_cortex	10779	9814
47	102	R_insular_cortex	8222	5599
48	121	L_cingulate_gyrus	14662	12490
49	122	R_cingulate_gyrus	16595	14489
50	161	L_caudate	1906	1608
51	162	R_caudate	2353	1997
52	163	L_putamen	3015	2622
53	164	R_putamen	2177	3758
54	165	L_hippocampus	3791	4454
55	166	R_hippocampus	3596	4673
56	181	cerebellum	174045	158617
57	182	brainstem	32567	28225

6.3) Urinary Fluoride Concentration in Cattle: The urinary fluoride concentration (ppm) was measured both for a sample of livestock grazing in an area previously exposed to fluoride pollution and also for a similar sample of livestock grazing in an unpolluted area.

Polluted	Unpolluted
21.3	10.1
18.7	18.3
21.4	17.2
17.1	18.4
11.1	20.0
20.9
19.7

6.4) To study whether the variances in certain time period (e.g. 1981 to 2006) of the consumer-price-indices (CPI) of several items were significantly different. Use the SOCR CPI dataset (http://wiki.socr.umich.edu/index.php/SOCR_Data_Dinov_021808_ConsumerPriceIndex) to answer this question for the Fuel, Oil, Bananas, Tomatoes, Orange juice, Beef and Gasoline items. (Apply the methods introduced in Differences of variances of independent samples).

References

• SOCR