SMHS NonParamInference
Contents
[hide]- 1 Scientific Methods for Health Sciences - Non-Parametric Inference
- 1.1 Overview
- 1.2 Motivation
- 1.3 Theory
- 1.4 Applications
- 1.5 Software
- 1.6 Problems
- 1.7 References
Scientific Methods for Health Sciences - Non-Parametric Inference
Overview
Nonparametric inference is descriptive and inferential statistics made that are not based on parametrized families of probability distributions, which is the basis of the parametric inference we discussed in HS 550. That is, nonparametric inference made no assumptions about the probability distributions of the variables assessed and the model structure is not specified a priori but is determined from data instead. The term nonparametric is not strictly referring to models completely lack of parameters but that the number and nature of the parameters are flexible and not fixed in advance. In this lecture, we are going to introduce to the area of nonparametric inference and illustrate various nonparametric inference applications with examples.
Motivation
We have discussed about parametric inference where the inference is made based on the assumptions of the probability distributions of the variables being assessed. What if such an assumption is violated and variables studied cannot be categorized into a parametrized family of probability distribution? Distribution-free (nonparametric) statistical methods would be the answer to solving problems in such situation.
Motivational Clinical Example: the relative risk of mortality from 16 studies of septic patients is reported, which measures whether the patients developed complications of acute renal failure. A relative risk of 1.0 means no effect and relative risk ≠1 suggests beneficial or detrimental effect of developing acute renal failure in sepsis. The main goal was to determine whether developing acute renal failure as a complication of sepsis impacts patient mortality from the cumulative evidence in these 16 studies and the data is recorded as below. The data is heavily skewed and not bell-shaped and apparently not normally distributed, so the traditional paired t-test is not applicable.
| Study | Relative Risk | Sign (Relative Risk -1) |
| 1 | 0.75 | - |
| 2 | 2.03 | + |
| 3 | 2.29 | + |
| 4 | 2.11 | + |
| 5 | 0.80 | - |
| 6 | 1.50 | + |
| 7 | 0.79 | - |
| 8 | 1.01 | + |
| 9 | 1.23 | + |
| 10 | 1.48 | + |
| 11 | 2.45 | + |
| 12 | 1.02 | + |
| 13 | 1.03 | + |
| 14 | 1.30 | + |
| 15 | 1.54 | + |
| 16 | 1.27 | + |
Theory
Differences of Median of Two Paired Samples: the sign test and the Wilcoxon signed rand test are the simplest nonparametric tests, which are also alternatives to the one-sample and paired t-test.
The Sign Test
The Sign Test is a nonparametric alternative to the One-Sample and Paired T-Test and doesn’t require the data to be normally distributed. It assigns a positive (+) or negative (-) sign to each observation according to whether it is greater or less than some hypothesized value. It measures the difference between the ± signs and how distinct the difference is from our expectations to observe by chance alone. For the motivational example, if there were no effects of developing acute renal failure on the outcome from sepsis, about half of the 16 studies above would be expected to have a relative risk less than 1.0 (a "-" sign) and the remaining 8 would be expected to have a relative risk greater than 1.0 (a "+" sign). In the actual data, 3 studies had "-" signs and the remaining 13 studies had "+" signs. Intuitively, this difference of 10 appears large to be simply due to random variation. If so, the effect of developing acute renal failure would be significant on the outcome from sepsis.
- Calculations: suppose \(N_{+}\) is the number of “+” signs and the significance level \(\alpha=0.05\); the hypotheses: \(H_{0}:N_{+}=8\); vs. \(H_{a}\): \(N_{+}≠8\) (the effect of developing acute renal failure is not significant on the outcome from sepsis vs. the effect of developing acute renal failure is significant on the outcome from sepsis). Define the following test statistics: \(B_{S}=max(N_{+},N_{-})\), where \(N_{+}\) and \(N_{-}\) are the number of positive and negative sings respectively. For the example above, we have \(B_{S}=max(N_{+},N_{-})=max(13,3)=13\) and the probability that such binomial variable exceeds 13 is \(P(B_{S}\ge 13 |B_{S} \sim Bin(16,0.5))=0.010635\). Therefore, we can reject the null hypothesis \(H_{0}\) and conclude that the significant effect of developing acute renal failure on the outcome from sepsis.
- Example: A set of 12 identical twins took a psychological test to determine whether the first born child tends to be more aggressive than the second born. Each twin is scored according to aggressiveness; a higher score indicates greater aggressiveness. Because of natural pairing in twins these data are paired.
| Twin-Index | 1st Born | 2nd Born | Sign |
| 1 | 86 | 88 | - |
| 2 | 71 | 77 | - |
| 3 | 77 | 76 | + |
| 4 | 68 | 64 | + |
| 5 | 91 | 96 | - |
| 6 | 72 | 72 | 0 (Drop) |
| 7 | 77 | 65 | + |
| 8 | 91 | 90 | + |
| 9 | 70 | 65 | + |
| 10 | 71 | 80 | - |
| 11 | 88 | 81 | + |
| 12 | 87 | 72 | + |
First plot the data using SOCR Linear Chart SOCR Linear Chart and observe that there seems to be no strong effect of the order of birth on baby’s regression.
Next, use the SOCR Sign Test Analysis to quantitatively evaluate the evidence to reject the null hypothesis that there is no birth-order effect on baby’s aggressiveness. (p-value of 0.274, implying we can’t reject the null hypothesis at 5% level of significance.)
The Wilcoxon Signed Rank Test
The Wilcoxon Signed Rank Test is used to compare differences between measurements. It requires that the data are measured at an interval level of measurements but does not require assumptions about the form of the distribution of the measurements. Therefore, it may be used whenever or not the parametric assumptions of the t-test are satisfied.
- Motivational example: data on the central venous oxygen saturation \((SvO_{2}(\%)\)) from 10 consecutive patients at 2 time points, at admission and 6 hours after admission to the intensive care unit (ICU) are recorded. \(H_{0}\): there is no effect of 6 hours of ICU treatment on \(SvO_{2}\), which implies that the mean difference between \(SvO_{2}\) at admission and that 6 hours after admission is approximately zero. The data are recorded as below:
| Patient | X_On_Admission | Y_At_6_Hours | X-Y_Diff(Treatment-Baseline) | \(|X-Y|_Diff\) | \((Rank)_{|X-Y|}\) | Signed_Rank |
|---|---|---|---|---|---|---|
| 10 | 65.3 | 59.8 | 5.5 | 5.5 | 4 | 4 |
| 2 | 59.1 | 56.7 | 2.4 | 2.4 | 1 | 1 |
| 7 | 58.2 | 60.7 | -2.5 | 2.5 | 2 | -2 |
| 9 | 56 | 59.5 | -3.5 | 3.5 | 3 | -3 |
| 3 | 56.1 | 61.9 | -5.8 | 5.8 | 5 | -5 |
| 5 | 60.6 | 67.7 | -7.1 | 7.1 | 6 | -6 |
| 6 | 37.8 | 50 | -12.2 | 12.2 | 7 | -7 |
| 1 | 39.7 | 52.9 | -13.2 | 13.2 | 8 | -8 |
| 4 | 57.7 | 71.4 | -13.7 | 13.7 | 9 | -9 |
| 8 | 33.6 | 51.3 | -17.7 | 17.7 | 10 | -10 |
| n=10 | W=-45 |
Result: the one-sided and two-sided alternative hypotheses p-values for the Wilcoxon Signed Rank Test reported by the SOCR Analysis are 0.011 and 0.022 respectively.
Result output and interpretation:
- Variable 1 = At_Admission
- Variable 2 = 6_Hrs_Later
- Results of Two Paired Sample Wilcoxon Signed Rank Test:
- Wilcoxon Signed-Rank Statistic = 5.000: [data-driven estimate of the Wilcoxon Signed-Rank Statistic]
- \(E(W_{+})\), Wilcoxon Signed-Rank Score = 27.500: [Wilcoxon Signed-Rank Score = expectation of the Wilcoxon Signed-Rank Statistic]
- \(Var(W_{+})\), Variance of Score = 96.250: [Variance of Score = variance of the Wilcoxon Signed-Rank Statistic]
- Wilcoxon Signed-Rank Z-Score = -2.293 \(\bigg \{Z_{score}=\frac{W_{stat}-E(W_{+})}{\sqrt{Var(W_{+})}} \bigg \}\)
- One-Sided P-Value = .011: [the one-sided (uni-directional) probability value expressing the strength of the evidence in the data to reject the null hypothesis that the two populations have the same medians (based on Gaussian, standard Normal, distribution)]
- Two-Sided P-Value = .022: [the double-sided (non-directional) probability value expressing the strength of the evidence in the data to reject the null hypothesis that the two populations have the same medians (based on Gaussian, standard Normal, distribution)].
Calculations: The original observations are assumed to be on an equal-interval scale. They are replaced by their ranks. This brings to focus the ordinal relationships among the measures — either "greater than" or "less than", leaving off the "equal to" paired measures. Why is the sum of the \(n\) unsigned ranks equal to \(\frac{n(n+1)}{2}\)?
The maximum possible positive value of the sum of all ranks, \(W\), when all signs are positive, is \(W=55\), and the minimum possible value, when all signs are negative, would be \(W=-55\). In this example, \(W=-45\), negative signs among the signed ranks suggest that \((SvO_{2}(\%)\)) levels 6-hrs later are larger. The null hypothesis is that there is no tendency in either direction, i.e., the numbers of positive and negative signs will be approximately equal. In that event, we would expect the value of \(W \sim 0\) subject to random variability. Let's look at a mock up example involving only \(n=3\) cases, where \(|X—X|\) differences are the untied ranks 1, 2, and 3. Here are the possible combinations of \(+\) and \(-\) signs distributed among these ranks, along with the value of W for each combination.
| (1) | (2) | (3) | W |
|---|---|---|---|
| + | + | + | +6 |
| - | + | + | +4 |
| + | - | + | +2 |
| + | + | - | 0 |
| - | - | + | 0 |
| - | + | - | -2 |
| + | - | - | -4 |
| - | - | - | -6 |
There are \(2^3= 8\) equally likely combinations. Exactly one yielding \(W=+6\), two yielding \(W\ge +4\), and etc. down to the other end of the distribution where one combination yields \(W=-6\). The probability \(P(W \ge +4)=\frac{2}{8}=0.25\). The "two-tailed" probability of \(P(|W| \ge 4)= \frac{2}{8}+\frac{2}{8} = 0.5\).
As the size of \(n\) increases, the shape of the distribution of \(W\) becomes closer to normal distribution. When the sample \(n\ge10\), the approximation is good enough to allow the use of the Z-statistic, for smaller \(n\), the observed value of \(W\) may be calculated exactly by using the sampling distribution as shown above in the case of \(n=3\).
The null hypothesis yields an expected value of \(W \sim 0\). The standard deviation \(W\) is given by: \(\sigma_W = \sqrt{ \frac{n(n+1)(2n+1)}{6}}.\)
The test statistics is \(Z= \frac{W \pm 0.5}{\sigma_W}\). The \(\pm 0.5\) is added as continuity correction, as \(W\) takes decimal values due to the artifact of the process of assigning tied ranks.
Assumptions of the Wilcoxon signed-rank test:
- The paired values of \(X\) and \(X\) are randomly and independently drawn (i.e., each pair is drawn independently of all other pairs)
- The dependent variable (in this example, central venous oxygen saturation) is intrinsically continuous, producing real-valued measurements
- The measures of \(X\) and \(Y\) have the properties of at least an ordinal scale of measurement, so that they can be compared (ranked) as "greater than" or "less than".
R Calculations
X_On_Admission <- c(65.3,59.1,58.2,56,56.1,60.6,37.8,39.7,57.7,33.6) Y_At_6_Hours <- c(59.8,56.7,60.7,59.5,61.9,67.7,50,52.9,71.4,51.3)
diff <- c(X_On_Admission - Y_At_6_Hours) #calculate the difference vector diff <- diff[ diff!=0 ] # delete all ties (differences equal to zero) diff diff.rank <- rank(abs(diff)) # get the absolute ranks of the differences diff.rank.sign <- diff.rank * sign(diff) # get the signs to the ranks, recalling the signs of the values of the differences ranks.pos <- sum(diff.rank.sign[diff.rank.sign > 0]) # calculate the sum of ranks assigned to the positive differences ranks.neg <- -sum(diff.rank.sign[diff.rank.sign < 0]) # get the sum of ranks assigned to the negative differences ranks.pos # The value W of the wilcoxon signed rank test [1] 5 ranks.neg [1] 50 wilcox.test(X_On_Admission, Y_At_6_Hours, paired=TRUE, alternative = "two.sided") # wilcox.test(X_On_Admission, Y_At_6_Hours, paired=TRUE, alternative = "two.sided", conf.int = T, conf.level = 0.95)
Wilcoxon-Mann-Whitney
Difference of Medians of Two Independent Samples can be analyzed using the Wilcoxon-Mann-Whitney (WMW) test, a nonparametric test of assessing whether two samples come from the same distribution.
- Motivational Example: 9 observations of surface soil acidity (pH) were made at two different independent locations. There is no pairing in this design though this is a balanced design with 9 observations in each group. The question is does the data suggest that the true mean soil pH values differ for the two locations. Let's assume a priori false-positive rate \(\alpha=0.05\) and validity of the assumptions for the test.
| Location1 | Location2 |
| 8.10 | 7.85 |
| 7.89 | 7.30 |
| 8.00 | 7.73 |
| 7.85 | 7.27 |
| 8.01 | 7.58 |
| 7.82 | 7.27 |
| 7.99 | 7.50 |
| 7.80 | 7.23 |
| 7.93 | 7.41 |
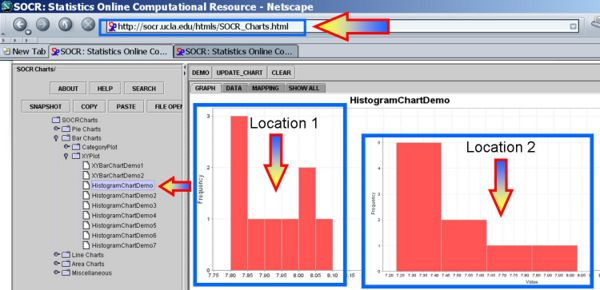
Plot the data and we can see that the distributions may be different or not even symmetric, unimodal and bell-shaped. Therefore, the assumptions of the independent t-test may be violated.
The first figure shows the index plot of the pH levels for both samples. The second figure shows the sample histograms of these samples, which are clearly not Normal-like. Therefore, the independent t-test would not be appropriate to analyze these data.
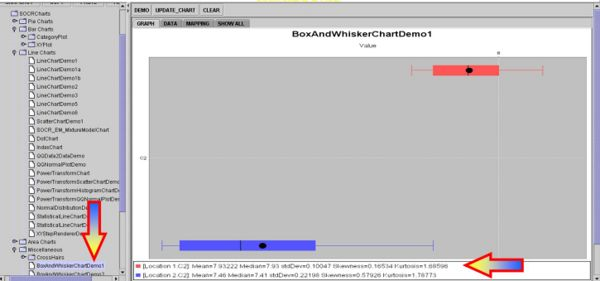
Intuitively, we may consider these group differences significantly large, especially if we look at the Box-and-Whisker Plots, but this is a qualitative inference that demands a more quantitative statistical analysis that can back up our intuition.
- The Wilcoxon-Mann-Whitney Test (WMW): a non-parametric test for assessing whether two samples come from the same distribution. The null hypothesis is that the two samples are drawn from a single population, and therefore that their probability distributions are equal. It requires that the two samples are independent, and that the observations are ordinal or continuous measurements.
- Calculations: The U statistic for the WMW test may be approximated for sample sizes above about 20 using the normal distribution. The U test is provided as part of SOCR analyses.
- For small samples: (1) Choose the sample for which the ranks seem to be smaller. Call this Sample 1, and call the other sample Sample 2; (2) For each observation in Sample 2, count the number of observations in Sample 1 that are smaller than it (count 0.5 for any that are equal to it); (3) The total sum of these counts is the statistics U.
- For larger samples: (1) Arrange all the observations into a single ranked series. That is, rank all the observations without regard to which sample they come from; (2) Let \(R_1\) be the sum of all the ranks in Sample 1. Note that the sum of ranks in Sample 2 can be easily calculated as the sum of all the ranks equals \(\frac{N (N + 1)}{2}\), where \(N=n_1 + n_2\) is the total number of observations in the two samples; (3) The U statistics is given by the formula: \(U_{1}=R_{1}-\frac{n_{1} (n_1+1)}{2}\), where \(n_{1}\(is the two sample size for Sample 1, and \(R_{1}\) is the sum of the ranks in Sample 1. There is no specification as to which sample is considered Sample 1. An equally valid formula for U is \(U_{2}=R_{2}-\frac{n_{2}(n_{2}+1)}{2}\), since the sum of the two values is given by \(U_{1}+U_{2}=R_{1}-\frac{n_{1}(n_{1}+1)}{2}+R_{2}-\frac{n_{2} (n_{2}+1)}{2}\). Given that \(R_{1}+R_{2}=\frac{N(N+1)}{2}\) and \(N=n_{1}+n_{2}\), hence we have \(U_{1}+U_{2}=n_{1} n_{2}\). The maximum value of U is the product of the sample sizes.
- Application using SOCR analyses: it is much quicker to use SOCR analyses to compute the statistical significance of the sign test.
Clearly the p value < 0.05 and therefore our data provides sufficient evidence to reject the null hypothesis. So we assume that there were significant PH differences between the two soil lots tested in this experiment.
- One-sided P-value for Sample 2 < Sample 1 = 0.00040.
- Two-sided P-value for Sample 1 not equal to Sample 2 = 0.00079.
- R Calculations
Location1 <- c(8.1,7.89,8,7.85,8.01,7.82,7.99,7.8,7.93) Location2 <- c(7.85,7.3,7.73,7.27,7.58,7.27,7.5,7.23,7.41) wilcox.test(Location1, Location2, paired=FALSE, alternative = "two.sided") [1] W = 78.5, p-value = 0.0009172
- SOCR WMW Critical scores Table. These critical values for the WMW test-statistics are computed using the following R-script
cat("n1", " n2 ")
for (a in c(1,5,10,100,200)) cat(a/2000, " ")
for (x in 4:20) {
for (y in 1:20) {
cat(x,y, "")
for (a in c(1,5,10,100,500)) {
cat(if (qwilcox(a/2000,x,y,lower.tail = TRUE,
log.p = FALSE)-1>=0) qwilcox(a/2000,x,y,lower.tail = TRUE,
log.p = FALSE)-1 else 0, " ")
}
cat("\n")
}
}
Note that if F(x) denotes the CDF of the Wilcoxon-Mann-Whitney \(U\) statistic, the R-function qwilcox computed the quantile function \(Q(α)=\inf\{x∈N:F(x)≥α\}, α∈(0,1)\), for \(U\). Since U is a discrete variable, for a given probability \(\alpha\), we can't always find a critical value \(x\) corresponding to \(\alpha\), i.e., \(F(x)=α\). However, there will be a minimum \(x\), such that \(F(x)= F(Q(α))>α\). If \(C(α)\) denotes the critical value for the WMW test, \(F(C(α))≤α\), to preserve the false-positive error rate of the test. Thus, \(C(α)=\sup\{x∈N:F(x)≤α\},α∈(0,1)\) and if there exists a value \(x\) such that \(F(x)=α\), then, \(C(α)=Q(α)\), otherwise, \(C(α)=Q(α)−1\).
The WMW Test vs. Independent T-test
Both types of tests answer the same question but they treat data differently.
- The WMW test uses rank ordering: Positive: Doesn’t depend on normality or population parameters Negative: Distribution free lacks power because it doesn't use all the info in the data
- The T-test uses the raw measurements: Positive: Incorporates all of the data into calculations Negative: Must meet normality assumption
- Neither test is uniformly superior. If the data are normally distributed we use the T-test. If the data are not normal use the WMW test.
McNemar Test
Depending upon whether the samples are dependent or independent different statistical tests may be appropriate.
- Differences of proportions of two independent samples: If the samples are independent and we are interested in the differences in the proportions of subjects of the same trait (a characteristic of each observation, e.g., gender) we need to use the standard proportion tests. For small sample sizes, we use corrected proportion \((\tilde p)\) that and we use the raw sample proportion \((\hat p)\) in large samples.
- Differences of proportions of two paired samples: If the samples are paired, then we can employ the McNemar's non-parametric test for differences in proportions in matched pair samples. It is most often used when the observed variable is a dichotomous variable (presence or absence of a trait/characteristic for each observation).
- Example: suppose a medical doctor is interested in determining the effect of a drug on a particular disease (D). Suppose the doctor conducts a study and records the frequencies of incidence of the disease (D+ and D− ) in a random population before the treatment with the new drug takes place. Then the doctor prescribes the treatment (e.g., an experimental vaccine against Ebolavirus) to all subjects and records the incidence of the disease in the rows following the treatment. The test requires the same subjects to be included in the before- and after-treatment measurements (matched pairs).
| Before Treatment | ||||
| D + | D − | Total | ||
| After Treatment | D + | a=101 | b=59 | a+b=160 |
| D − | c=121 | d=33 | c+d=154 | |
| Total | a+c=222 | b+d=92 | a+b+c+d=314 | |
- Marginal homogeneity occurs when the row totals equal to the column totals, a and d in each equation can be cancelled; leaving b equal to c: a+b=a+c, c+d=b+d. In this example, marginal homogeneity would mean there was no effect of the treatment.
- The McNemar statistic is shown: \(χ_{0}^{2}=\frac{(b-c)^{2}}{b+c} \simχ_{df=1}^{2}\).
- The marginal frequencies are not homogeneous if the \(χ_{0}^{2}\) result is significant (say at \(p < 0.05\)). If b and/or c are small \((b + c < 20)\) then \(χ_{0}^{2}\) is not approximated by the Chi-Square Distribution and a Sign Test should be used instead.
- An interesting observation when interpreting McNemar's test is that the elements of the main diagonal contribute no information whatsoever to the decision, i.e., in the above example, pre- or post-treatment condition is more favorable.
- See the Section on Positive and Negative Predictive values and the Chi-square goodness-of-fit and bivariate association tests.
- R Calculations:
x<-matrix(c(101, 59, 121, 33),2,2) mcnemar.test(x) McNemar's Chi-squared test with continuity correction McNemar's chi-squared = 20.6722, df = 1, p-value = 5.45e-06 # From first principles # “d” returns the height of the probability density function # “p” returns the cumulative density function # “q” returns the inverse cumulative density function (quantiles) # “r” returns randomly generated numbers (59-121)^2/(59+121) [1] 21.35556 1-pchisq(21.35556,df=1)
General McNemar test of marginal homogeneity for a single category
If we have observed measurements on a K-level categorical variable -- e.g., agreement between two evaluators summarized by a \(K×K\) classification table, where each row or column contains the number of individuals rated as part of this group by each evaluator. For instance, two instructors may evaluate students as 1=poor, 2=good and 3=excellent. There could be significant differences in the evaluations of the same students by the 2 instructors. Suppose we are interested in whether the proportions of students rated excellent by the 2 instructors are the same. Then we'll pool the poor and good categories together and form a 2x2 table that we can then use the 2x2 McNemar test statistics on, as shown below.
| Evaluator 2 | |||||
| Poor | Good | Excellent | Total | ||
| Evaluator 1 | Poor | 5 | 15 | 4 | 24 |
| Good | 16 | 10 | 9 | 35 | |
| Excellent | 11 | 17 | 13 | 41 | |
| Total | 32 | 42 | 26 | 100 | |
| Evaluator 2 | ||||
| Poor | Good or Excellent | Total | ||
| Evaluator 1 | Poor | a=5 | b=19 | a+b=24 |
| Good or Excellent | c=27 | d=49 | c+d=76 | |
| Total | a+c=32 | b+d=68 | a+b+c+d=100 | |
- To test marginal homogeneity for one single category (in this case poor evaluation) means to test row/column marginal homogeneity for the first category (poor). This is achieved by collapsing all rows and columns corresponding to the other categories.
- \(χ_{o}^{2}=\frac{(b-c)^{2}}{b+c}=\frac{(-8)^{2}}{46}=1.39\sim χ_{df=1}^{2}\)
- \(P( χ_{df=1}^{2}>1.39)=0.238405\)
- Therefore, we don’t have sufficient evidence to reject the null hypothesis of two evaluators were consistent in their ratings of students.
R Calculations:
x<-matrix(c(5, 19, 27, 49),2,2) mcnemar.test(x) # From first principles # “d” returns the height of the probability density function # “p” returns the cumulative density function # “q” returns the inverse cumulative density function (quantiles) # “r” returns randomly generated numbers (27-19)^2/(27+19) [1] 1-pchisq(1.391304,df=1)
Kruskal-Wallis Test
Multi-sample inference, based on differences of means of several independent samples, as discussed in ANOVA, may still be appropriate in situations where ANOVA assumptions are invalid.
- Motivational Example: Suppose four groups of students are randomly assigned to be taught with four different techniques, and their achievement test scores are recorded. Are the distributions of test scores the same, or do they differ in location? The data is presented in the table below. The small sample sizes and the lack of distribution information of each sample illustrate how ANOVA may not be appropriate for analyzing these types of data.
| Teaching Method | ||||
| Index | Method1 | Method2 | Method3 | Method4 |
| 1 | 65 | 75 | 59 | 94 |
| 2 | 87 | 69 | 78 | 89 |
| 3 | 73 | 83 | 67 | 80 |
| 4 | 79 | 81 | 62 | 88 |
The Kruskal-Wallis Test is the non-parametric analogue of One-Way Analysis of Variance, using data ranking. It is a non-parametric method for testing equality of two or more population medians. Intuitively, it is identical to a One-way Analysis of Variance with the raw data (observed measurements) replaced by their ranks. Since it is a non-parametric method, the Kruskal-Wallis Test does not assume a normal population, unlike the analogous one-way ANOVA. However, the test does assume identically-shaped distributions for all groups, except for any difference in their centers (e.g., medians).
- Calculations: Let N be the total number of observations and \(N=\sum_{i=1}^{k}n_{i}\) and \(R(X_{ij})\) be the rank assigned to \(X_{ij}\) and let \(R_{i}\) be the sum of ranks assigned to the \(i^{th}\) sample and \(R_{i}=\sum_{j=1}^{n_i} R(X_{ij}),\) for each \(i=1,2,…,k.\)
- The SOCR program computes \(R_{i}\) for each sample. The test statistic is defined for the following formulation of hypotheses:
- \(H_{o}\): All of the \(k\) population distribution functions are identical.
- \(H_{a}\): At least one of the populations tends to yield larger observations than at least one of the other populations.
- Suppose \({X_{i,1},X_{i,2},…,X_{i,n_i}}\) represents the values of the \(i^{th}\) sample, where \(i\le i\le k.\)
- Test statistics: \(T=(\frac{1}{S^{2}})\sum_{i=1}^{k}\frac{R_{i}^{2}}{n_{i}}-\frac{N(N+1)^{2}}{4}\), where \(S^{2}=\frac{\Bigg(\frac{1}{N-1}\sum R(X_{ij})^{2}-N(N+1)\Bigg)^{2}}{4}.\)
- Note: If there are no ties, then the test statistic is reduced to:
- \(T=\frac{12}{N(N+1)} \sum_{i=1}^{k}\frac{R_{i}^{2}}{n_{I}} -3(N+1).\)
- However, the SOCR implementation allows for the possibility of having ties; so it uses the non-simplified, exact method of computation. Multiple comparisons have to be done here. For each pair of groups, the following is computed and printed at the Result Panel.
- \(|\frac{R_{i}}{n_{i}}-\frac{R_{j}}{n_{j}}|\) > \(t_{1-\frac{\alpha}{2}}\frac{\Bigg(\frac{S^{2}(N-1-T)}{N-K}\Bigg)^{\frac{1}{2}}}{\Bigg(\frac{1}{n_{i}} +\frac{1}{n_{j}}\Bigg)^{\frac{1}{2}}}\)
- The SOCR computation employs the exact method instead of the approximate one (Conover 1980), since computation is easy and fast to implement and the exact method is somewhat more accurate.
- The Kruskal-Wallis Test Using SOCR Analyses: It is much quicker to use SOCR Analyses to compute the statistical significance of this test. This SOCR Kruskal-Wallis Test Activity may also be helpful in understanding how to use this test in SOCR. For the teaching-methods example above, we can easily compute the statistical significance of the differences between the group medians (centers):
- Clearly, there is only one significant group difference between medians, after the multiple testing correction, for the group1 vs. group4 comparison (see below):
Group Method1 vs. Group Method2: 1.0 < 5.2056 Group Method1 vs. Group Method3: 4.0 < 5.2056 Group Method1 vs. Group Method4: 6.0 > 5.2056 Group Method2 vs. Group Method3: 5.0 < 5.2056 Group Method2 vs. Group Method4: 5.0 < 5.2056 Group Method3 vs. Group Method4: 10.0 > 5.2056
- R Calculations: Using SOCR Kruskal-Wallis Analysis Example 1 dataset.
group1 <- c(83,91,94,89,89,96,91,92,90) group2 <- c(91,90,81,83,84,83,88,91,89,84) group3 <- c(101,100,91,93,96,95,94) group4 <- c(78,82,81,77,79,81,80,81) kruskal.test(list(group1, group2, group3, group4))
Alternatively,
group1 <- c(83,91,94,89,89,96,91,92,90)
group2 <- c(91,90,81,83,84,83,88,91,89,84)
group3 <- c(101,100,91,93,96,95,94)
group4 <- c(78,82,81,77,79,81,80,81)
data <- c(group1, group2, group3, group4)
factors <- factor(rep(1:4, c(length(group1), length(group2), length(group3), length(group4))),
labels = c("Group1", "Group2", "Group3", "Group4"))
kruskal.test(data, factors)
# or using formula interface
kruskal.test(data~factors)
Fligner-Killeen test: Variance Homogeneity (Differences of Variances of Independent Samples)
Different tests for variance equality can be applied. It is frequently necessary to test if \(k\) samples have equal variances. Homogeneity of variances is often a reference to equal variances across samples. Some statistical tests, for example the analysis of variance, assume that variances are equal across groups or samples.
- Calculation: The (modified) Fligner-Killeen test (the median-centering Fligner-Killeen test) provides the means for studying the homogeneity of variances of k populations \(\big\{X_{ij}\), for \(1\le i \le n_{j}\) and \(1 \le j \le k\big\}.\) The test jointly ranks the absolute values of \(|X_{ij}-\tilde X_{j}|\) and assigns increasing scores \(a_{N,i}=\Phi^{-1} \left( \frac{1+\frac{i}{N+1}}{2}\right)\), based on the ranks of all observations. In this test, \(\tilde X_{j}\) is the sample median of the \(j^{th}\) group, and \(\Phi\)(.) is the cumulative distribution function for Normal distribution.
- Fligner-Killeen test statistics: \(χ_{o}^{2}=\frac{\sum_{j=1}^{k}n_{j}(\overline A_{j}-\bar a)^{2}} {V^{2}}\) , where \(\overline A_{j}\) is the mean score for the \(j^{th}\) sample, \(\bar a\) is the overall mean score of all \(a_{Nj}\) and \(V^{2}\) is the sample variance of all scores. We have \(N=\sum_{j=1}^{k}n_{j},\overline A_{j}=\frac{1}{n_{j}}\sum_{j=1}^{n_j}a_{N,m_i}\), where \(a_{N,m_i}\) is the increasing rank score for the \(i^{th}\) observation in the \(j^{th}\) sample, \(\bar a=\frac {1}{N} \sum_{i=1}^{N}a_{N,i},V^{2}=\frac{1}{N-1}\sum_{i=1}^{N}(a_{N,i}-\bar a)^{2}\) .
- Fligner-Killeen probabilities: for large sample size, the modified Fligner-Killeen test statistic has an asymptotic chi-square distribution with \(k-1\) degrees of freedom \(χ_{o}^{2} \sim χ_{k-1}^{2}\).
- R calculations: Using SOCR Fligner-Killeen Analysis Example 1 dataset.
group1 <- c(83,91,94,89,89,96,91,92,90) group2 <- c(91,90,81,83,84,83,88,91,89,84) group3 <- c(101,100,91,93,96,95,94) group4 <- c(78,82,81,77,79,81,80,81) fligner.test(list(group1, group2, group3, group4))
Applications
- This article presents a general introduction to nonparametric inference and the model involved and studied the existence of complete and sufficient statistics for this model. It gives an empirical process estimating the model and generalized the empirical cumulative hazard rate from survival analysis. Consistency and weak convergence results were given and tests for comparison of two counting processes, generalizing the two sample rank tests are defined and studied. Finally, it gives an application to a set of biological data.
- This article presents a study relates a different solution to the challenge of constructing a sequence of functions, each based on only finite segments of the past, which together provide a strongly consistent estimator for the conditional probability of the next observation, given the infinite past. It also studied on some extensions to regression, pattern recognition and on-line forecasting.
Software
Problems
6.1) Suppose 10 randomly selected rats were chosen to see if they could be trained to escape a maze. The rats were released and timed (seconds) before and after 2 weeks of training (N means the rat did not complete the maze-test). Do the data provide evidence to suggest that the escape time of rats is different after 2 weeks of training? Test using α = 0.05.
| Rat | Before | After | Sign |
| 1 | 100 | 50 | + |
| 2 | 38 | 12 | + |
| 3 | N | 45 | + |
| 4 | 122 | 62 | + |
| 5 | 95 | 90 | + |
| 6 | 116 | 100 | + |
| 7 | 56 | 75 | - |
| 8 | 135 | 52 | + |
| 9 | 104 | 44 | + |
| 10 | N | 50 | + |
6.2) Automated brain volume segmentation is an important step in many modern computational brain mapping studies. Suppose we have two separate and competing versions of automated brain parsing (segmentation) algorithms that automatically tessellate (partition) the brain into 57 separate regions of interest (ROI’s). An important question then is how consistent are these 2 different techniques, across the 57 ROIs. We can use the ROI volume as a measure of the resulting automated brain parcellation and compare the paired differences between the 2 methods across all ROIs. The image shows an example of a brain parcellated into these 57 regions and the table below contains the volumes of the 57 ROIs for the 2 different brain tessellation techniques. Use appropriate SOCR analyses and relevant SOCR charts to argue whether or not the 2 different methods are consistent and agree on their ROI labels.
| Index | Volume_Intensity | ROI_Name | Method1_Volume | Method2_Volume |
| 1 | 0 | Background | 9236455 | 9241667 |
| 2 | 21 | L_superior_frontal_gyrus | 78874 | 78693 |
| 3 | 22 | R_superior_frontal_gyrus | 69575 | 74391 |
| 4 | 23 | L_middle_frontal_gyrus | 67336 | 68872 |
| 5 | 24 | R_middle_frontal_gyrus | 68344 | 67024 |
| 6 | 25 | L_inferior_frontal_gyrus | 31912 | 21479 |
| 7 | 26 | R_inferior_frontal_gyrus | 26264 | 29035 |
| 8 | 27 | L_precentral_gyrus | 28942 | 33584 |
| 9 | 28 | R_precentral_gyrus | 35192 | 30537 |
| 10 | 29 | L_middle_orbitofrontal_gyrus | 10141 | 11608 |
| 11 | 30 | R_middle_orbitofrontal_gyrus | 9142 | 11850 |
| 12 | 31 | L_lateral_orbitofrontal_gyrus | 7164 | 5382 |
| 13 | 32 | R_lateral_orbitofrontal_gyrus | 5964 | 4947 |
| 14 | 33 | L_gyrus_rectus | 3840 | 1995 |
| 15 | 34 | R_gyrus_rectus | 2672 | 2994 |
| 16 | 41 | L_postcentral_gyrus | 24586 | 27672 |
| 17 | 42 | R_postcentral_gyrus | 21736 | 28159 |
| 18 | 43 | L_superior_parietal_gyrus | 25791 | 27500 |
| 19 | 44 | R_superior_parietal_gyrus | 28850 | 32674 |
| 20 | 45 | L_supramarginal_gyrus | 16445 | 22373 |
| 21 | 46 | R_supramarginal_gyrus | 11893 | 11018 |
| 22 | 47 | L_angular_gyrus | 20740 | 22245 |
| 23 | 48 | R_angular_gyrus | 20247 | 17793 |
| 24 | 49 | L_precuneus | 14491 | 12983 |
| 25 | 50 | R_precuneus | 15589 | 16323 |
| 26 | 61 | L_superior_occipital_gyrus | 6842 | 6106 |
| 27 | 62 | R_superior_occipital_gyrus | 5673 | 6539 |
| 28 | 63 | L_middle_occipital_gyrus | 15011 | 19085 |
| 29 | 64 | R_middle_occipital_gyrus | 19063 | 25747 |
| 30 | 65 | L_inferior_occipital_gyrus | 10411 | 8675 |
| 31 | 66 | R_inferior_occipital_gyrus | 12142 | 12277 |
| 32 | 67 | L_cuneus | 6935 | 9700 |
| 33 | 68 | R_cuneus | 7491 | 11765 |
| 34 | 81 | L_superior_temporal_gyrus | 29962 | 34934 |
| 35 | 82 | R_superior_temporal_gyrus | 30630 | 28788 |
| 36 | 83 | L_middle_temporal_gyrus | 27558 | 19633 |
| 37 | 84 | R_middle_temporal_gyrus | 26314 | 25301 |
| 38 | 85 | L_inferior_temporal_gyrus | 24817 | 24885 |
| 39 | 86 | R_inferior_temporal_gyrus | 25088 | 20661 |
| 40 | 87 | L_parahippocampal_gyrus | 6761 | 6977 |
| 41 | 88 | R_parahippocampal_gyrus | 6529 | 7964 |
| 42 | 89 | L_lingual_gyrus | 16752 | 14748 |
| 43 | 90 | R_lingual_gyrus | 20914 | 18500 |
| 44 | 91 | L_fusiform_gyrus | 16565 | 15020 |
| 45 | 92 | R_fusiform_gyrus | 14409 | 17311 |
| 46 | 101 | L_insular_cortex | 10779 | 9814 |
| 47 | 102 | R_insular_cortex | 8222 | 5599 |
| 48 | 121 | L_cingulate_gyrus | 14662 | 12490 |
| 49 | 122 | R_cingulate_gyrus | 16595 | 14489 |
| 50 | 161 | L_caudate | 1906 | 1608 |
| 51 | 162 | R_caudate | 2353 | 1997 |
| 52 | 163 | L_putamen | 3015 | 2622 |
| 53 | 164 | R_putamen | 2177 | 3758 |
| 54 | 165 | L_hippocampus | 3791 | 4454 |
| 55 | 166 | R_hippocampus | 3596 | 4673 |
| 56 | 181 | cerebellum | 174045 | 158617 |
| 57 | 182 | brainstem | 32567 | 28225 |
6.3) Urinary Fluoride Concentration in Cattle: The urinary fluoride concentration (ppm) was measured both for a sample of livestock grazing in an area previously exposed to fluoride pollution and also for a similar sample of livestock grazing in an unpolluted area.
| Polluted | Unpolluted |
| 21.3 | 10.1 |
| 18.7 | 18.3 |
| 21.4 | 17.2 |
| 17.1 | 18.4 |
| 11.1 | 20.0 |
| 20.9 | |
| 19.7 |
6.4) To study whether the variances in certain time period (e.g. 1981 to 2006) of the consumer-price-indices (CPI) of several items were significantly different. Use the SOCR CPI dataset to answer this question for the Fuel, Oil, Bananas, Tomatoes, Orange juice, Beef and Gasoline items. (Apply the methods introduced in Differences of variances of independent samples).